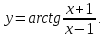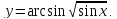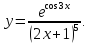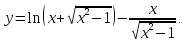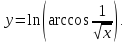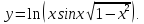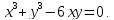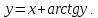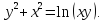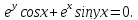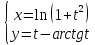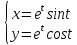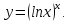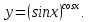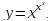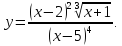- •Диффернцирование функции одной переменной.
- •Правила дифференцирования.
- •2. Производная сложной функции.
- •3. Производная функции, заданной неявно.
- •4. Производная функции, заданной параметрически.
- •5. Производная степенно-показательной функции.
- •6. Производные высших порядков.
- •7. Дифференциал функции.
- •7.1 Вычисление дифференциала.
- •7.2 Применение дифференциала к приближенным вычислениям.
- •7.3 Дифференциалы высших порядков.
- •8. Правило Лопиталя – Бернулли.
- •8.2 Раскрытие неопределенности типа .
- •8.3 Раскрытие неопределенности типа .
- •8.4 Раскрытие неопределенностей типа .
- •9. Уравнения касательной и нормали.
- •1. К параболе в точке, абсцисса которой
- •11. Наибольшее и наименьшее значения функции.
- •12. Промежутки выпуклости и вогнутости. Точки перегиба.
- •13. Общая схема исследования функций и построения графиков.
- •13.1 Общая схема исследования и построения графика функции заданной явно.
- •13.2 Общая схема исследования и построения графика функции заданной параметрически.
Диффернцирование функции одной переменной.
Производной
данной функции
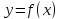 по аргументу
по аргументу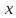 назывется предел отношения приращения
функции
назывется предел отношения приращения
функции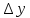 к приращению аргумента
к приращению аргумента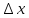 , когда последнее произвольным образом
стремится к нулю:
, когда последнее произвольным образом
стремится к нулю:

Операция
нахождения производной от функции
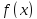 называетсядифференцированием
этой функции.
называетсядифференцированием
этой функции.
Правила дифференцирования.
Если
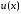 и
и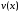 являются дифференцируемыми функциями
аргумента
являются дифференцируемыми функциями
аргумента ,
то:
,
то:
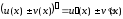 (1)
(1)
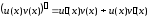 (2)
(2)
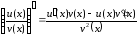 (3)
(3)
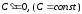 (4)
(4)
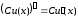 (5)
(5)
Таблица производных элементарных функций:
|
|
Функция
|
Производная
функции
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
1 |
|
|
|
1 |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
Задания 1. Найти производные функции:
|
1.
|
2. |
|
3. |
4. |
|
5. |
6. |
|
7. |
8. |
|
9. |
10. |
|
11.
|
12. |
|
13.
|
14.
|
|
15. |
16. |
|
17. |
18. |
|
19. |
20. |
|
21.
|
22. |
2. Производная сложной функции.
Если
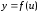 и
и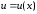 являются дифференцируемыми функциями
своих аргументов, то производная сложной
функции
являются дифференцируемыми функциями
своих аргументов, то производная сложной
функции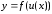 существует и равна произведению
производной данной функции
существует и равна произведению
производной данной функции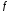 по промежуточному аргументу
по промежуточному аргументу на производную промежуточного аргумента
на производную промежуточного аргумента по независимой переменной :
по независимой переменной :
 (6)
(6)
В
случае
 ,
,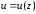 ,
,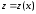 :
:
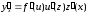 (7)
(7)
Аналогично во всех более сложных случаях.
Пример 1
Найти
производную функции

Решение:
Аргументом
данной функции
 является
является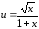
Используя таблицу производных, имеем:
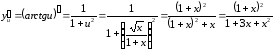 .
.
Производную
функции
 по переменной
по переменной найдем, используя правило дифференцирования
частного (3) и таблицу производных:
найдем, используя правило дифференцирования
частного (3) и таблицу производных:
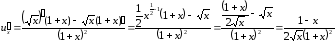
Таким образом, получаем, согласно (6):
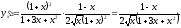
Ответ:
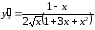
Задания 2. Найти производные функции:
|
1.
|
2. |
|
3. |
4. |
|
5. |
6. |
|
7. |
8. |
|
9. |
10. |
|
11.
|
12. |
|
13.
|
14.
|
|
15. |
16. |
|
17. |
18. |
|
19. |
20. |
|
21.
|
22. |
3. Производная функции, заданной неявно.
Пусть
зависимость между
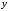 и
и задана в виде соотношения:
задана в виде соотношения:
 (8)
(8)
В
этом случае говорят, что функция
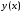 задана неявно.
задана неявно.
Для
вычисления производной
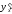 необходимо:
необходимо:
а)
вычислить производные от обеих частей
уравнения (8), считая при этом
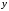 функцией от
функцией от ;
;
б) приравнять полученные производные;
в)
решить полученное уравнение относительно
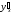 .
.
Пример 2
Найти
производную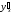 ,
если
,
если
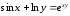
Решение:
а)
вычисляем производные от обеих частей
заданного равенства, считая
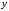 функцией от
функцией от :
:
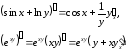
б) приравниваем полученные производные:

в)
решаем уравнение относительно
 :
:
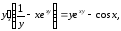
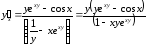
Ответ:

4. Производная функции, заданной параметрически.
Функция
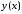 является
заданной параметрически, если
является
заданной параметрически, если и
и заданы как функции параметра
заданы как функции параметра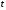 :
:
 (9)
(9)
Если
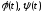 - дифференцируемые функции и
- дифференцируемые функции и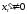 ,
то производная
,
то производная может быть найдена по формуле:
может быть найдена по формуле:
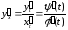 (10)
(10)
Пример 3
Найти
производную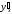 ,
если
,
если
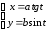
Решение:
Находим
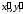 :
:
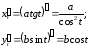
Воспользовавшись формулой (10), получаем:
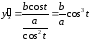
Ответ:

5. Производная степенно-показательной функции.
Рассмотрим
степенно-показательную функцию
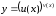 .
.
Для
вычисления производной
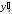 предварительно прологарифмируем
предварительно прологарифмируем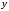 :
:
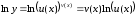
Продифференцируем
обе части полученного равенства, считая
при этом
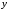 функцией от
функцией от :
:
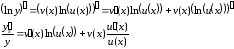
Разрешая
полученное уравнение относительно
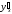 ,
окончательно получаем:
,
окончательно получаем:
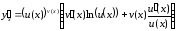 (11)
(11)
Пример 4
Найти
производную функции
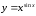
Решение:
Прологарифмируем заданную функцию:

Продифференцируем
обе части полученного равенства по
 :
:
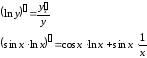
Приравниваем полученные производные:
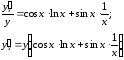
Учитывая явный вид заданной функции, окончательно получаем:

Ответ:
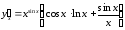
Задания 3. Найти производные функции:
|
1.
|
2. |
|
3. |
4. |
|
5. |
6. |
|
7. |
8. |
|
9. |
10. |
|
11.
|
12. |
|
13.
|
14.
|
|
15. |
16. |
|
17. |
18. |

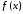
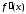

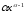
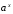
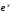
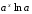
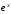
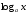
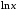
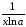
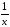
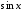
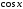

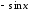

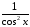
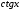

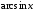
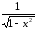
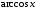
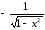
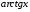
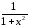




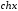
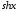
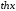
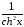
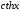
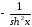
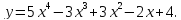

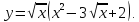

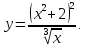
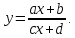
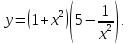
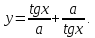
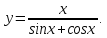
 .
.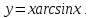
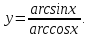
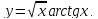
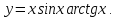

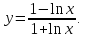
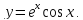
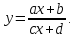
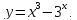
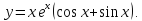
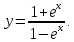
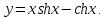
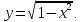
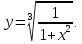


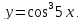
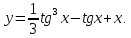
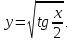
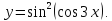
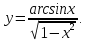
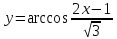 .
.