Примеры.

1. ,, А рядсходится – это сумма бесконечно убывающей геометрической прогрессии.

2. , начиная с определенного номераn>Nвыполнено , а гармонический рядрасходитсярасходится и исходный ряд.

3. - ряд с неотрицательными членами.

приn.

Но ряд сходится, значит по первому признаку сравнения сходится и исходный ряд.

4. - ряд с отрицательными членами, но если мы докажем сходимость ряда, то мы тем самым докажем сходимость исходного ряда.приnисходный ряд сходится.

5. - ряд с положительными членами, т.к.приn=3,4,… и(под логарифмом стоит число, большее единицы). Учитывая, чтоприn, получим асимптотику членов исходного ряда

,

т.о. исходный ряд эквивалентен гармоническому и расходится.

3. Признаки Коши и Даламбера для рядов с неотрицательными членами.

Достаточными признаками сходимости рядов с положительными членами являются признаки Даламбера и Коши.

Признак Даламбера. Пусть- ряд с положительными членамиa_n>0 итогда

1. при l<1 рядсходится,

2. при l>1 ряд расходится,

3. при l=1 ничего сказать нельзя.

Доказательство.

1. Если l<1, тоl<1-2l+<1-.

Т.к.  , то>0N():l-<a_n+1/a_n<l+<1-=q<1 дляn>N()

 a_n+1  a_nq,

тогда

a_N+1  a_N q

a_N+2  a_N+1 q  a_N q²

………………………

a_N+p  a_N+p-1 q … a_N q^p

Ряд a_N q+ a_N q+…+ a_N q^p+… сходится, как сумма бесконечно убывающей геометрической прогрессии со знаменателем 0<q<1по признаку сравнения сходится и исходный ряд.

2. Если l>1, тоl>1+2=>l->1+.

Т.к.  , тоN(): 1+<l-<<l+дляn>N()

=> для n>N, тогда

a_N+1  a_N

a_N+2 a_N+1 a_N

………………………

Т.о. члены ряда ограничены снизу положительной постоянной a_N>0 и не стремятся к 0ряд расходится.

3) рассуждения не применимы при l=1

Замечание.Признак Даламбера можно использовать для исследования сходимости рядов с произвольными комплексными членами. Действительно, еслито

при l<1 ряд сходится- сходится, причем абсолютно

2) при l>1 ряд- расходится

3) при l=1 ничего сказать нельзя.

Признак Коши(радикальный) Пусть- ряд с неотрицательными членамиa_n 0 итогда

1. при l<1 рядсходится,

2. при l>1 ряд расходится,

3. при l=1 ничего сказать нельзя.

Доказательство.

1. если l<1, тоl<1-2=>l+<1-. Т.к., то из последовательности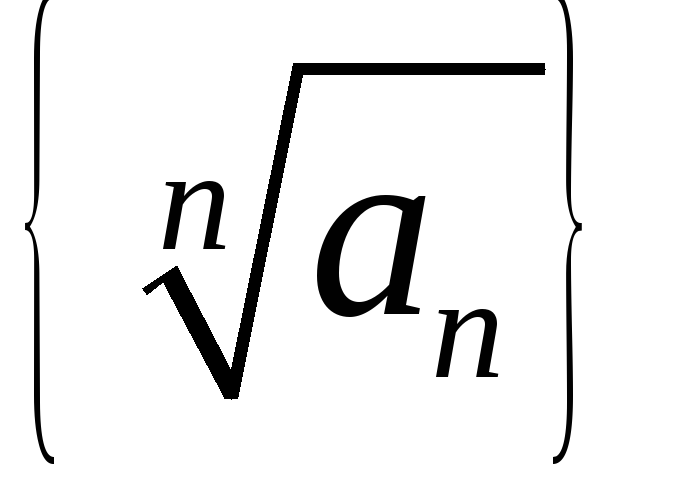можно выделить подпоследовательность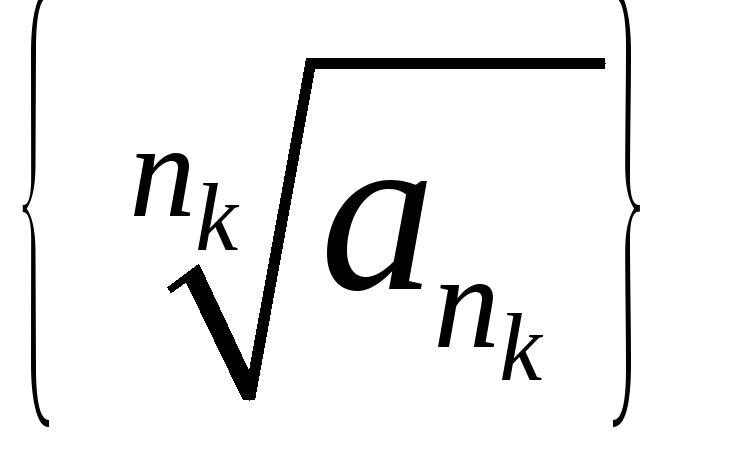, сходящуюся кl. Причемl наибольшая по величине точка сгущения последовательности

т.о. N():

<l+<1-=q<1, дляn>N().

иначе бы существовала другая, большая по величине точка сгущения .

=>a_n<qⁿ, т.е. ряд мажорируется бесконечно убывающей геометрической прогрессией со знаменателемq<1.

2) Если l>1, тоl>1+=>l->1.

Т.к.  , тоN():l-<дляn_k>N()

=> => >1 => бесконечное число членов ряда больше 1 => члены ряда не стремятся к 0 => ряд расходится.

3) рассуждения не применимы при l=1.

Замечание.Радикальный признак Коши можно использовать для исследования сходимости рядов с произвольными комплексными членами. Действительно, еслито

при l<1 ряд сходится- сходится абсолютно

2) при l>1 ряд- расходится

3) при l=1 ничего сказать нельзя.

Замечание 3.Если о рядеизвестно лишь, что или то о сходимости действительно ничего сказать нельзя. Например, рядыиудовлетворяют обоим условиям. При этом один из них сходится, а другой расходится.

Интегральный признак Коши.Если функцияипри, то ряд

,

сходится тогда и только тогда, когда сходится несобственный интеграл

.

Доказательство.

 kпри, в силу убывания

.

Проинтегрируем неравенство по отрезку

.

Суммируя эти неравенства от k=1 доk=n, получим

.

Полагая - частичные суммы ряда, получим

.

1) Если несобственный интеграл сходится, то при n=>

.

Т.е. последовательность частичных сумм ряда с неотрицательными членами ограничена сверху ряд сходится.

2. Если ряд с неотрицательными членами сходится, то при n=>

.

Для при : 1n в силу неотрицательности

.

Т.о. совокупность интегралов ограничена=> несобственный интегралсходится.

3) Если расходится, то, но тогда из неравенстваследует, чтои рядрасходится по определению.

4) Если ряд расходится, тои согласно неравенствувыполнено, что означает расходимость несобственного интеграла.

Примеры.

1. -ряд Дирихле.

,

верхняя подстановка конечна, если =>

Ряд Дирихле сходится при и расходится при.

2. - расходится, т.к.

- расходится.