§13. Признаки Дирихле и Абеля для рядов с произвольными комплексными членами.

Докажем некоторые достаточные признаки сходимости рядов.

Предварительно рассмотрим одно преобразование сумм

Такое преобразование частичных сумм называется преобразованием Абеля. С его помощью докажемнеравенство Абеля.

Лемма (неравенство Абеля). Еслии, то

.

Доказательство.

Т.к. 

Важно, что оценка дается модулем первого и последнего члена и не зависит от числа слагаемых.

Замечание.Доказательство проходит и в случае. Т.е. можно потребовать просто монотонности.

Признак Дирихле. Пусть дан ряд: последовательность {a_n} – монотонно стремится к 0, а последовательность частичных сумм{B_n} ряда- ограничена, тогда ряд- сходится.

Доказательство.



  N():n>N()

Теперь применяем неравенство Абеля

.

Согласно критерию Коши ряд сходится.

__________________

Докажем, что частичные суммы иограничены при(припервая сумма равна 0, а вторая не ограничена).

Действительно

Сумма первых n членов геометрической последовательности с первым членоми знаменателеместь

Действительная и мнимая части этого выражения не превосходят.

Примеры.

1. . Последовательность {1/n} – монотонно стремится к нулю. А последовательность- ограниченапо признаку Дирихле исходный ряд сходится.

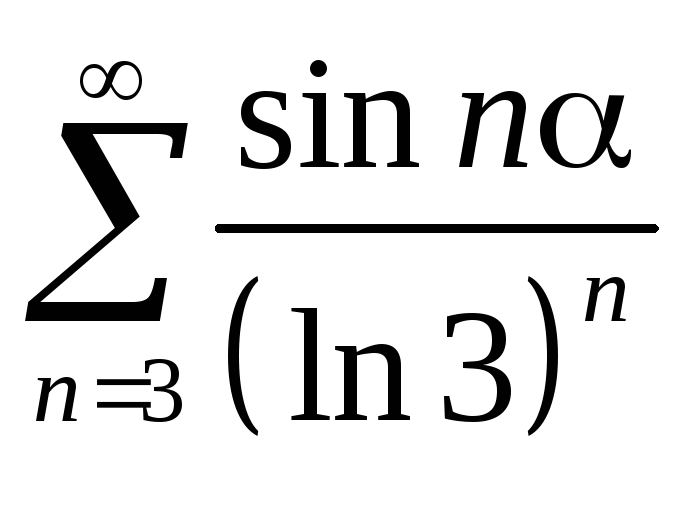2. 3.

Признак Абеля. Если последовательность {a_n} монотонна и ограничена, а рядсходится, то ряд из произведенийтакже сходится.

Доказательство.

М:

Выберем произвольное . Из сходимостиN():n>N()p>0

. Тогда согласно неравенству Абеля

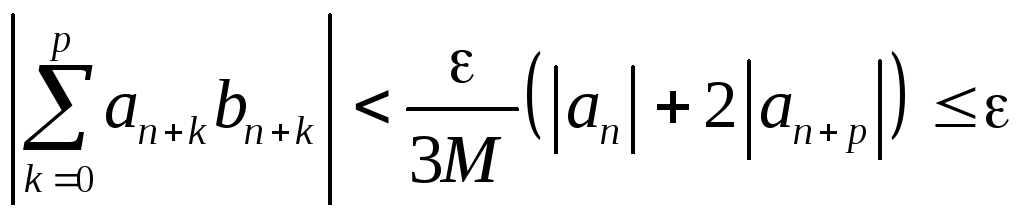
Согласно критерию Коши ряд сходится.

Пример.

Ряд сходится по признаку Дирихле. А последовательностьограничена и монотонна по признаку Абеля исходный ряд сходится.

§14. Функциональные последовательности и ряды.

1. Понятие равномерной сходимости функциональных последовательностей и рядов.

Рассмотрим последовательности и ряды, членами которых являются функции. Такие последовательности {u _k(z)} и рядыназываютсяфункциональными.

Разложение функций в ряды, члены которых, вообще говоря, проще, чем разлагаемая функция, используется при вычислении и исследовании функций, при интегрировании, решении дифференциальных уравнений и играет важную роль в прикладной математике. При этом существенно используется понятие равномернойсходимости и сходимости всреднем.

Пусть дана последовательность {u_k(z)} функций,zg. При фиксированномэто обычная числовая последовательность. Функциональная последовательностьназываетсясходящейся в точке, если числовая последовательностьсходится. Множество всех точек сходимости функциональной последовательностиназываетсяобластью сходимостифункциональной последовательности. Предел этой последовательности, вообще говоря, зависит от точки:- является функцией.

Определение.Последовательность функцийназывается (поточечно) сходящейся к функции, если>0 иzgN(,z):

.

Определение.Последовательность функцийназываетсяравномерносходящейся к функции, если>0 иzgN():

.

Это определение, очевидно, эквивалентно следующему

Определение.Последовательность функцийназываетсяравномерносходящейся к функции, если:

.

Обозначение равномерной сходимости .

В частном случае для функции понятие равномерной сходимости имеет простой геометрический смысл: начиная с достаточно большого графики всех функций последовательности лежат в «-полосе», окружающей график предельной функции.

Примеры.

1. Последовательность . Эта сходимость является равномерной, т.к.

Таким образом .

2. Последовательность на сегментесходится к разрывной функции

.

Сходимость эта неравномерная, что, в частности, понятно из геометрической интерпретации равномерной сходимости. На графике приведены графики функций последовательности, жирная линия – график предельной функции, имеющей разрыв первого рода в точке . В случае разрывной функции «-полоса» так же разрывна и для любого номераграфик функции, выходя из точки (0,0), приходит в точку (1,1) и при некоторомобязательно покинет «-полосу», окружающую предельную функцию.

3. Последовательность . Найдем максимально отклонение членов функциональной последовательности от предела.

Таким образом, , значит сходимость неравномерная.

Все вышесказанное легко приносится на ряды. Выражение - называетсяфункциональным рядом, заданным в g. Последовательность его частичных сумм образует функциональную последовательность.

Определение.Функциональный ряд называется сходящимся (поточечно), если сходится (поточечно) функциональная последовательность его частичных сумм.

Предел функциональной последовательность частичных сумм называется суммой сходящегося функционального ряда , аr_n(z)=S(z)--n-ый остаток функционального ряда.

Если функциональный ряд сходится, то >0N(,z): |r_n(z)| <дляn>N(,z).

Если функциональная последовательность частичных сумм функционального ряда сходится равномерно, то и функциональный ряд называется равномерносходящимся.

Определение.Если для>0N() : |r_n(z)| <дляn>N() иz одновременно, то рядu_k(z)называетсяравномерно сходящимсяк функцииf(z)в g. Обозначение:u_k(z)=>f(z).Пример.

- знакочередующийся ряд, сходится и признаку Лейбница, остаток ряда не превышает модуля следующего слагаемого

иx.

Всякой функциональной последовательности можно поставить в соответствие функциональный ряд, для которого исходная последовательность является последовательностью частичных сумм. Т.о. исследование равномерной сходимости функциональных рядов и последовательностей удобно рассматривать вместе, так как одно из другого вытекает в силу определения.