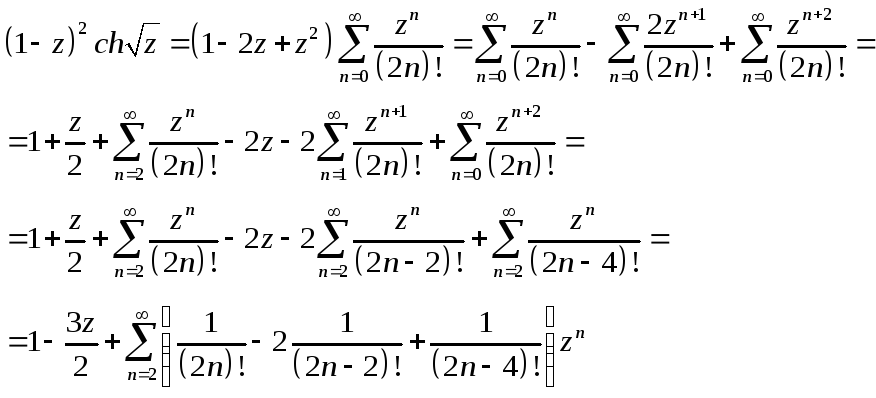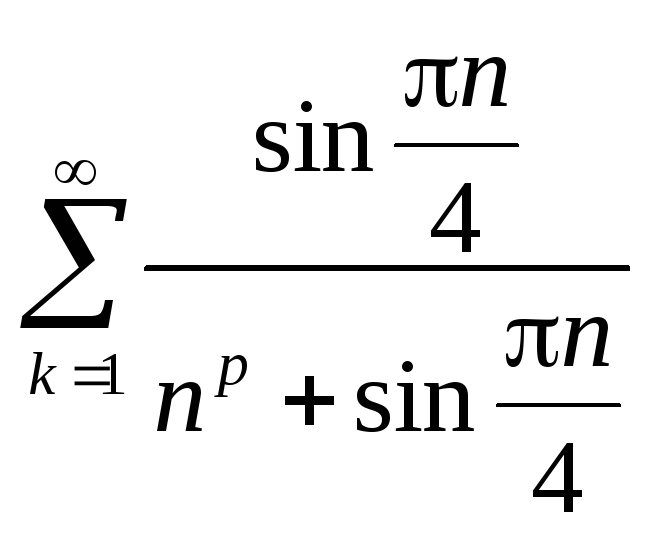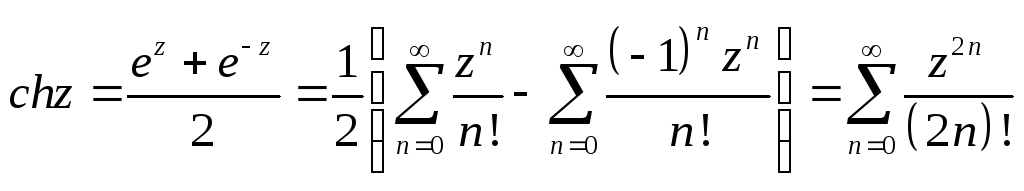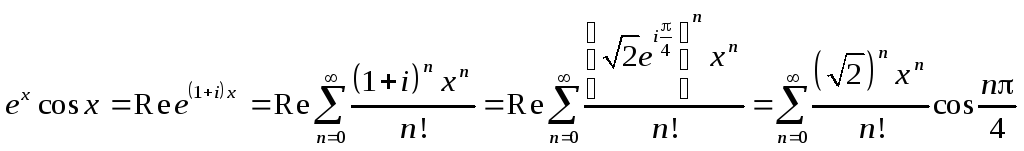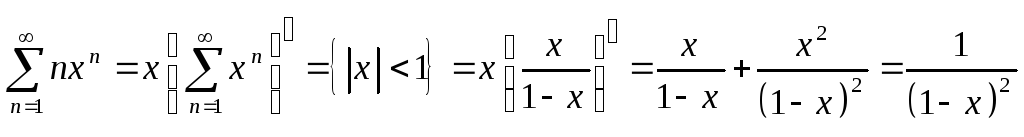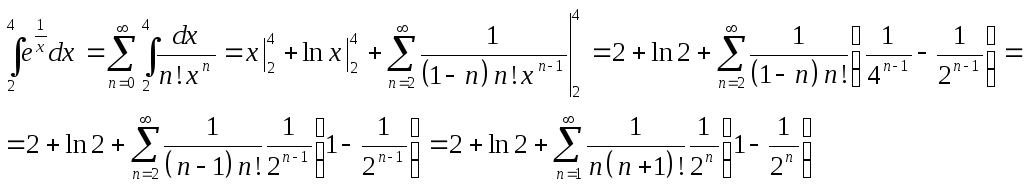Лекции / семестр3 / Альшина (МП-2) / Примеры решения задач на ряды
.docПримеры решения задач на ряды.
Числовые ряды.
-
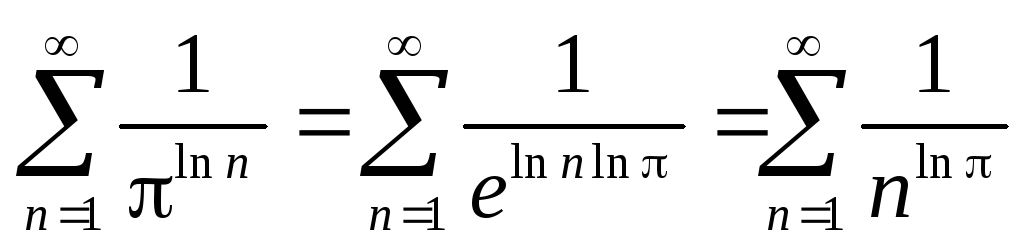 (сходится
(сходится
 )
) -
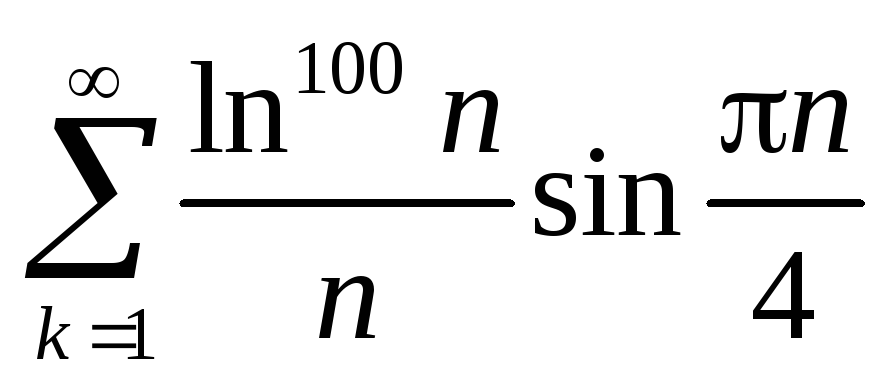 (сходится
по Дирихле)
(сходится
по Дирихле) -
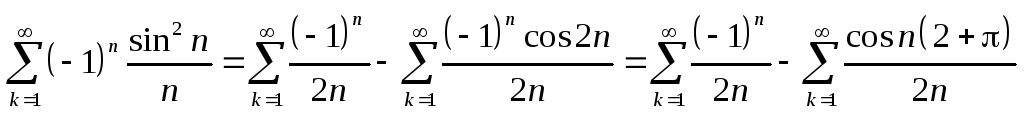
К исходному ряду признак Лейбница не применим из-за несоблюдения монотонности
Полученные два ряда сходятся, первый по Лейбницу, строй – по Дирихле.
К исходному ряду нельзя применить
признак Дирихле из-за немонотонности.
При
![]() общий
член ряда не убывает, поэтому ряд
расходится.
общий
член ряда не убывает, поэтому ряд
расходится.
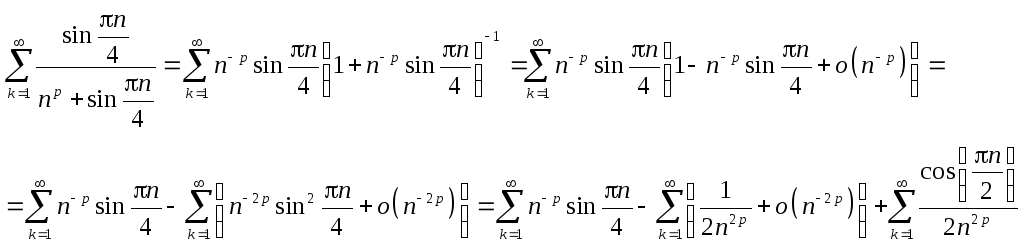
Первый и третий ряд сходятся по Дирихле
![]() ,
а второй сходится только для
,
а второй сходится только для
![]() .
Т.е. исходный ряд сходится только для
.
Т.е. исходный ряд сходится только для
![]() p>0.5.
p>0.5.
Нельзя применить признак сравнения, т.к. ряд знакочередующийся.
![]() - сходится по Дирихле, а
- сходится по Дирихле, а
![]() - монотонно возрастающая, ограниченная.
Т.о. применим признак Абеля.
- монотонно возрастающая, ограниченная.
Т.о. применим признак Абеля.
Последовательность
![]() - монотонна и ограничена, своим верхним
пределом
- монотонна и ограничена, своим верхним
пределом
![]() .
Поэтому к исходному ряду применим
признак Абеля, для чего необходимо
доказать сначала сходимость ряда
.
Поэтому к исходному ряду применим
признак Абеля, для чего необходимо
доказать сначала сходимость ряда
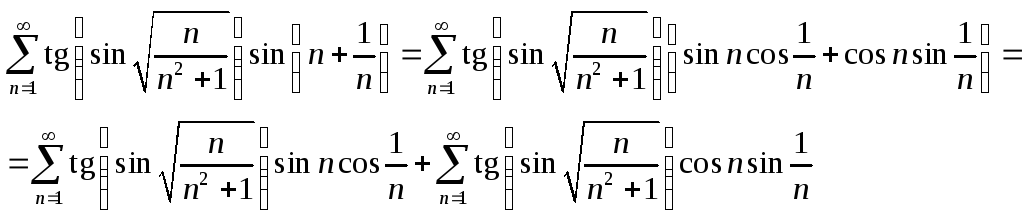
Каждая из последовательностей
![]() и
и
![]() монотонна и ограничена, а каждый из
рядов
монотонна и ограничена, а каждый из
рядов
![]() и
и
![]()
сходится по Дирихле.
Т.о. ряд
![]() сходится по признаку Абеля.
сходится по признаку Абеля.
Функциональные ряды.
-
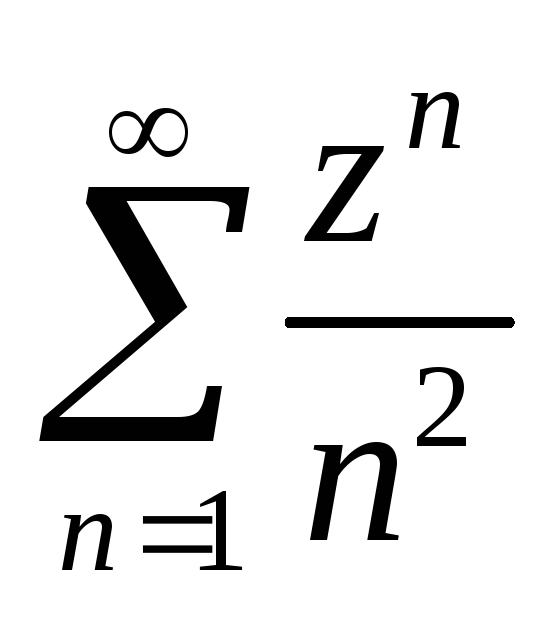 сходится только при
сходится только при
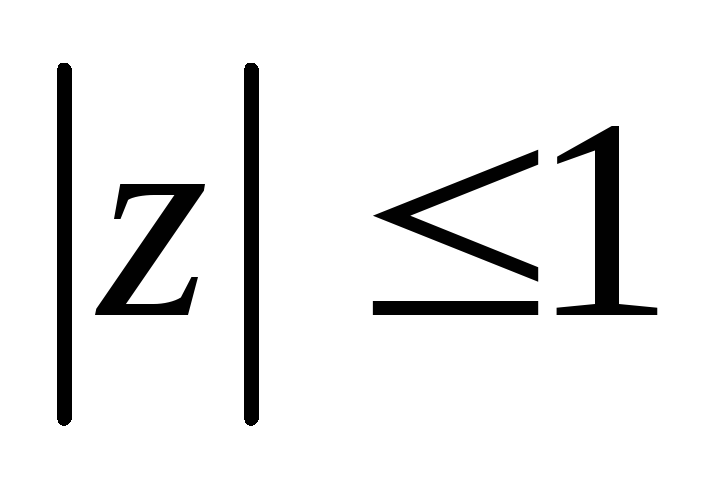 ,
иначе член ряда не убывает. Сходимость
равномерная в силу мажорантного признака
Вейерштрасса.
,
иначе член ряда не убывает. Сходимость
равномерная в силу мажорантного признака
Вейерштрасса. -
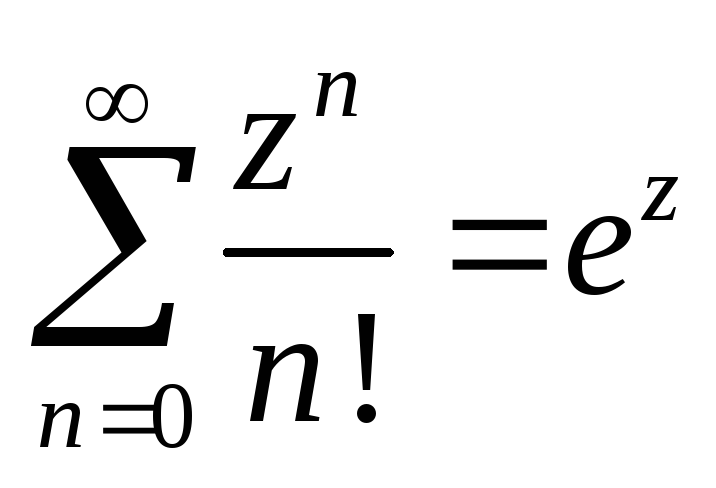 ряд сходится, причем равномерно в любом
круге
ряд сходится, причем равномерно в любом
круге
 ,
т.к. мажорируется сходящимся числовым
рядом
,
т.к. мажорируется сходящимся числовым
рядом
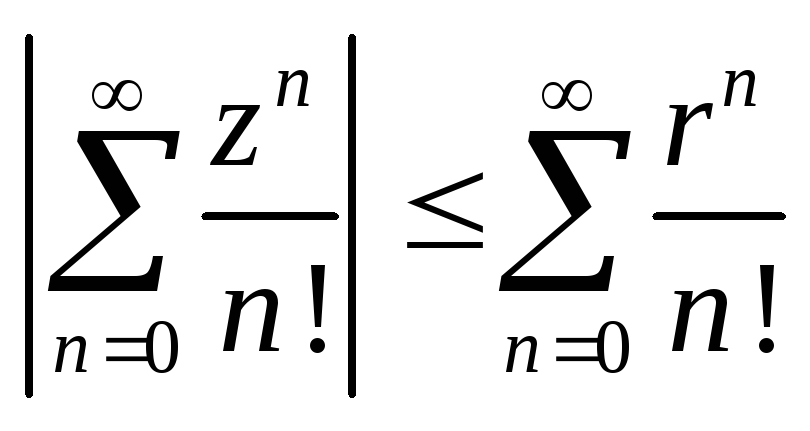 .
В силу произвольности r
ряд сходится на всей комплексной
плоскости. Но равномерной сходимости
на всей комплексной плоскости нет, т.к.
для
.
В силу произвольности r
ряд сходится на всей комплексной
плоскости. Но равномерной сходимости
на всей комплексной плоскости нет, т.к.
для
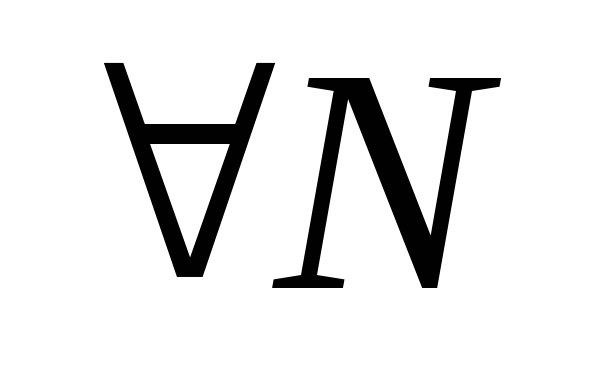 -фиксированного
и
-фиксированного
и
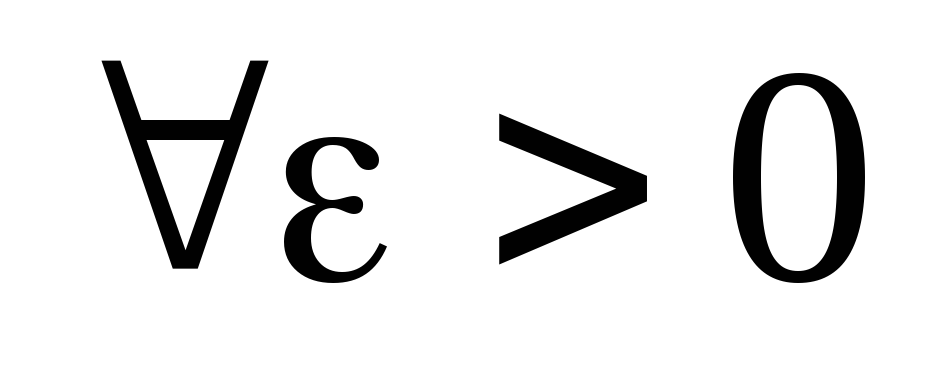 найдется такое
найдется такое
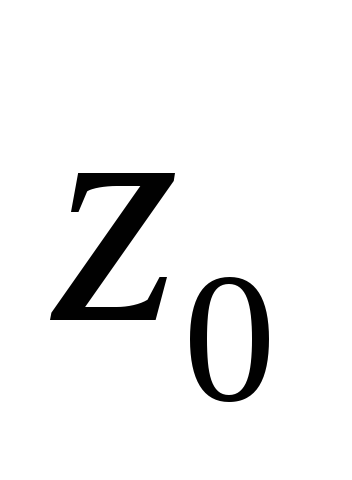 ,
что
,
что
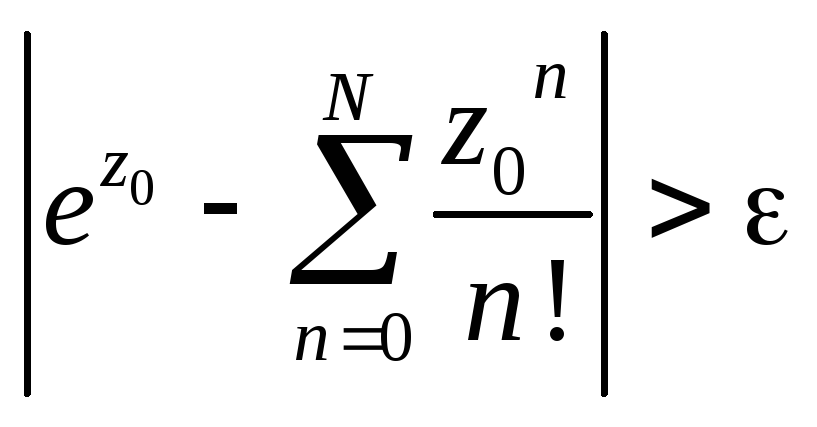 .
Это неравенство выполнено, т.к. в
частности на действительной оси
.
Это неравенство выполнено, т.к. в
частности на действительной оси
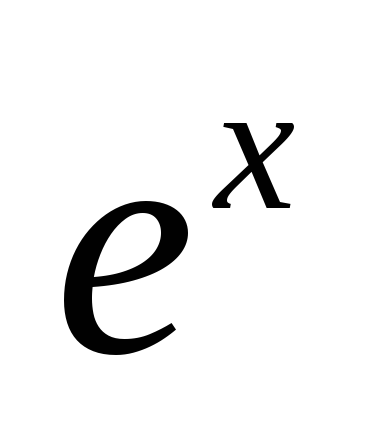 растет быстрее любой степенной функции,
следовательно
растет быстрее любой степенной функции,
следовательно
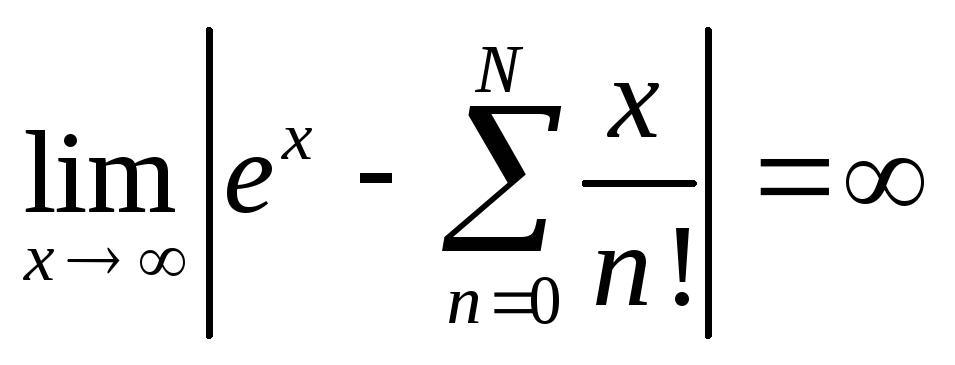 .
. -
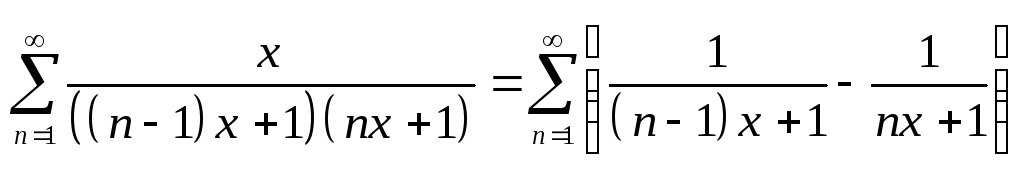
Найдем частичную сумму ряда
![]() .
.
![]() для
для
![]() .
Для x=0
сумма ряда 0. Т.о. ряд из непрерывных
функций сходится, но сходимость
неравномерная, т.к. сумма ряда разрывна.
.
Для x=0
сумма ряда 0. Т.о. ряд из непрерывных
функций сходится, но сходимость
неравномерная, т.к. сумма ряда разрывна.
При
![]() - фиксированного
- фиксированного
![]() при
при
![]() .
Т.о. ряд сходится.
.
Т.о. ряд сходится.
Для исследования равномерной
сходимости применим критерий Коши.
Пусть =1,
p=n,
![]() ,
тогда
,
тогда
![]() .
Т.о. сходимость неравномерная.
.
Т.о. сходимость неравномерная.
Степенные ряды.
![]()
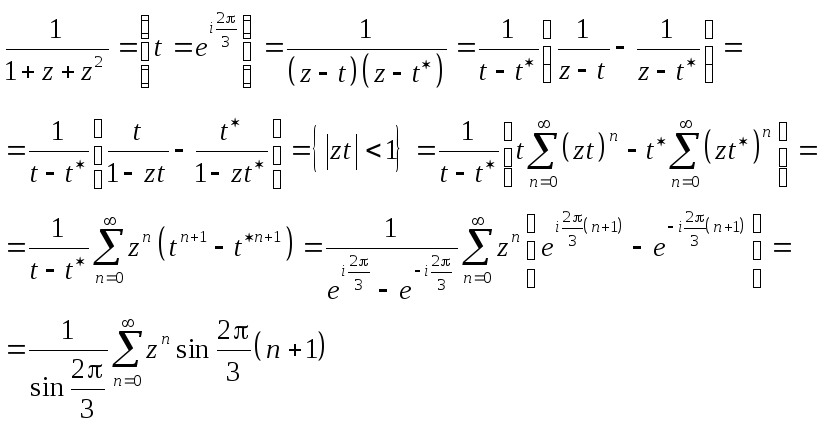

C=0, arcsin0=0
![]()