Порядок выполнения работы

1. Ознакомиться с методическими указаниями к лабораторной работе.

2. Проанализировать последовательность выполнения процедур быстрых преобразований.

3. Составить матричные соотношения для реализации быстрых преобразований.

4. Написать последовательность выводов программы при обработке тестовых данных.

5. Оформить отчет.

СОДЕРЖАНИЕ ОТЧЕТА

1. Титульная страница: названия вуза, кафедры, дисциплины, лабораторной работы (с её порядковым номером); Ф.И.О. и группа студента, Ф.И.О. преподавателя, дата.

2. Методическая страница: краткое описание теории.

3. Результаты аппроксимации.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Аппроксимация функций.

2. Понятие прямого быстрого дискретного преобразования Фурье.

3. Понятие обратного быстрого дискретного преобразования Фурье.

4. Понятие прямого и обратного быстрого дискретного преобразования Уолша-Адамара.

Литература

1.Вычислительная математика: методические указания к лабораторным работам/Рязан.гос.радиотехн.ун-т; сост. А.Н. Кабанов, Рязань,2008.-48 с.

2.Метод псевдообращения в задачах управления: Методические указания к лабораторной работе. Сост. А.Н. Кабанов. Рязань,1997.-16c.

3.Исследование вычислительных алгоритмов: Методические указания к лабораторной работе. Сост. А.Н. Кабанов. Рязань,1998.-20c.

4. Вычислительная математика: методические указания к лабораторным работам/Рязан.гос.радиотехн.ун-т;сост.Ю.И.Малинин,Рязань,2008.-48 с.

ЛАБОРАТОРНАЯ РАБОТА №5

Методы аппроксимации функций на основе функций гибкой структуры

(объем часов - 2)

Цель работы: Исследование параметрического метода аппроксимации

функций заранее заданной структуры.

В результате выполнения лабораторной работы студент:

должен знать :

1.алгоритм выбора масштабного коэффициента системы функций.

2.Формирование матриц преобразования для оперативной аппроксимации функций.

должен иметь представление о методах повышения оперативности спектрального анализа

должен уметь оценивать точность методов аппроксимации.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Параметрические методы аппрксимации сигналов, идентификации и анализа линейных систем управления широко распространены благодаря возможности получить корректное решение. В большинстве случаев корректности решения добиваются за счёт ограничения числа определяемых параметров, обеспечивающих минимум некоторого критерия близости модели и объекта. Удобной формой описания производственного процесса является представление его в виде некоторой функции заранее заданной структуры. Наблюдаемый процесс аппроксимируется функцией

, (3)

где (4)

и T1 – параметры, подлежащие определению.T1 выступает в роли масштабного коэффициента и оказывает существенное влияние на точность аппроксимации при ограниченном числе коэффициентов. Априорный выборT1 не всегда обеспечивает достаточную точность аппроксимации.

За критерий близости исходного процесса и аппроксимирующей функции примем квадратичный критерий

. (5)

Можно подбирая параметры ,i=1,2,…,N;, найти их значения, обеспечивающие минимум выбранного критерия (5). Однако этот путь сложный, длительный, так как потребует многократного численного вычисления интеграла (5).

Ставится задача– на основе оценок, определённых из условия минимума критерия (5) только при двух различных значениях ,а именно и , определить «истинные» значения параметров процессаT1 и ,.

При такой постановке задачи в качестве измеряемых величин выступают уже не значения наблюдаемого процесса, а оценки коэффициентов

(6)

и

, (7)

определённые из условия минимума критерия (5) при двух различных масштабах времени и, т. е. «измеряемые» величины могут быть представлены в виде:

, (8)

, (9)

где (10)

. (11)

Подставляя в уравнения (8), (9) вместо Y(t)его аппроксимирующее выражение из (3), получаем

, (12)

где (13)

. (14)

Задавшись некоторым значением из (12), определим оценку. Эта оценка зависит от двух параметровT21,.

, (15)

где (16)

Аналогично, задавшись тем же значением из (12), определим оценку . Эта оценка будет зависеть от двух параметровT22,.

. (17)

Здесь (18)

При оценкиисовпадут (при отсутствии помех). На практике за истинное значениеT1 принимается значение, при котором величина квадратичного критерия

Q=[-][-]=(19)

принимает минимальное значение.

Коэффициенты матриц ,i=1,2 зависят лишь от отношенияT1/T21в уравнении (16) и от отношенияT1/T22 в уравнении (18). Матрицымогут быть протабулированы заранее для выбранной системы функций. Коэффициенты матрицдля различныхN в представлении (1) и дляT22/T21=10 представлены в файлеМасштаб.xls. Таким образом, алгоритм определенияT1 сводится к последовательному вычислению выражений (15) и (17) при различных значенияхи определению минимума критерия (19).

За истинное значение вектора целесообразно принять среднее значение двух оценок

=1/2 [+] (20)

или ту оценку, которая соответствует значению T2i, ближайшему кT1. Однако желательно при найденном оптимальном значении Т1 произвести вычисление оценок.

Рассмотрим методику определения «истинного» масштаба T1 на следующем примере.

Наблюдаемый процесс имеет вид

, (21)

то есть С1=1; T1=6.

1. Задавшись =2 и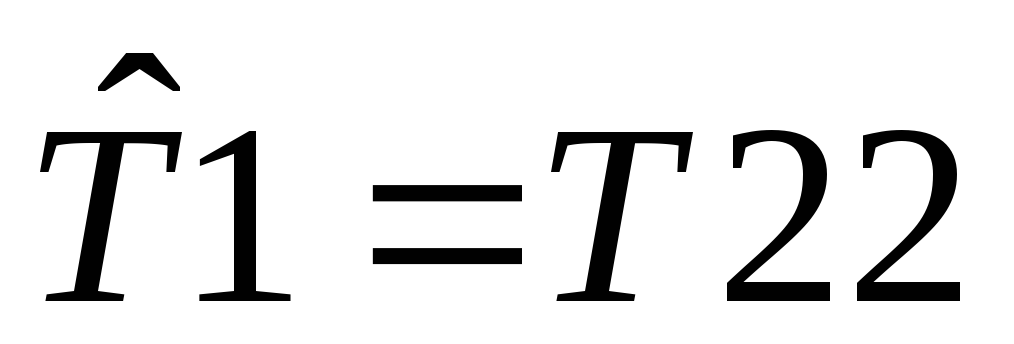=20, определяем векторы

, (22)

. (23)

Вычисления этих векторов могут производиться или непосредственно по формулам (8), (9) или значения этих векторов могут быть получены в результате эксперимента над исследуемым объектом.

(24)

. (25)

2. Придавая T1 значенияT1=1,2,…,10, производим вычисления

. (26)

. (27)

. (28)

и т. д. (29)

3. При каждом значении T1 вычисляем ошибку в определении параметров(30)

и величину критерия . (31)

Результаты вычислений сведены в таблицу 2.

Таблица 2.

Результаты вычислений

T1
1	1,00000	5,50000	1,5	0,4615	1,50000	2,53825	-1,03825		1,07796
2	0,75000	3,00000			1,12500	1,38450	-0,25950		0,06734
3	0,66667	2,16667			1,00000	0,99992	0,00008		0,00000
4	0,62500	1,75000			0,93750	0,80763	0,12988		0,01687
5	0,60000	1,50000			0,90000	0,69225	0,20775		0,04316
6	0,58333	1,33333			0,87500	0,61533	0,25967		0,06743
7	0,57143	1,21429			0,85714	0,56039	0,29675		0,08806
8	0,56250	1,12500			0,84375	0,51919	0,32456		0,10534
9	0,55556	1,05556			0,83333	0,48714	0,34619		0,11985
10	0,55000	1,00000			0,82500	0,46150	0,36350		0,13213

Значение T1, обеспечивающее минимальное значение критерияQ, обозначаем черезTT.

В данном случае TT=3.

4. Вычисляем истинное значение T1 по формуле

T1=TT*T21. (32)

T1=3*2=6 (33)

=1/2*(1,0000+0,99992)=0,99996. (34)

Таким образом, функция имеет вид:

. (35)

Таблицы матриц преобразования С1, С2

для экспоненциальной системы функций при Т21=1,Т22=10

C1(4*4)T1=1				C2(4*4)T1=1
1,00000	0,00000	0,00000	0,00000	717,01630	213,01280	80,95230	35,69280
0,00000	1,00000	0,00000	0,00000	-10816,20540	-3014,95040	-1061,53740	-426,25440
0,00000	0,00000	1,00000	0,00000	30928,15440	8458,98240	2917,05040	1144,82469
0,00000	0,00000	0,00000	1,00000	-22439,64030	-6081,64480	-2076,99030	-806,74880
C1(4*4)T1=2				C2(4*4)T1=2
0,00000	0,00000	-0,28125	-0,70313	80,43840	20,96640	6,85440	2,53440
1,00000	0,00000	2,14286	5,00000	-852,05120	-187,38720	-46,67520	-10,06720
0,00000	0,00000	-5,15625	-10,82813	2120,94720	446,51520	105,42720	21,26263
0,00000	1,00000	4,28571	7,50000	-1428,13440	-294,69440	-68,00640	-13,35840
C1(4*4)T1=3				C2(4*4)T1=3
0,00000	-0,49931	-1,87243	-3,20988	25,31841	5,67700	1,52510	0,42935
0,00000	3,16872	10,86420	17,92593	-199,62569	-31,05859	-2,65482	2,05535
1,00000	-6,66667	-20,00000	-31,42857	440,74030	63,53013	4,87630	-3,20320
0,00000	4,99314	11,98354	17,65432	-277,66358	-38,71562	-2,85182	1,77776
C1(4*4)T1=4				C2(4*4)T1=4
0,00000	-2,15820	-5,54967	-8,41699	11,71170	2,20220	0,45045	0,07508
0,00000	11,48438	27,84375	41,13281	-70,76160	-5,91360	1,81440	1,81440
0,00000	-20,00195	-44,90234	-64,29199	140,40810	10,40060	-2,60015	-1,67152
1,00000	11,66667	23,57143	32,50000	-83,28320	-5,87253	1,37280	0,80080
C1(4*4)T1=5				C2(4*4)T1=5
-0,29568	-5,51936	-12,08064	-17,23392	6,56250	1,00000	0,13393	0,00000
1,67552	26,38944	55,29216	77,31328	-30,62500	0,00000	1,87500	1,00000
-3,44448	-41,33376	-82,09344	-112,1916	55,12500	0,00000	-1,87500	0,00000
3,06432	21,45024	39,83616	53,02368	-30,93750	0,00000	0,88393	0,00000
C1(4*4)T1=6				C2(4*4)T1=6
-1,11175	-11,11754	-22,23508	-30,57324	4,10261	0,48266	0,02709	-0,00985
5,61728	49,43210	95,49383	129,19753	-14,59800	1,50274	1,34940	0,42935
-9,84375	-72,18750	-133,87500	-177,89063	23,99040	-1,88160	-0,63360	0,80640
6,33745	34,85597	61,56379	80,16872	-12,78883	0,91349	0,26100	-0,22837
C1(4*4)T1=7				C2(4*4)T1=7
-2,657226	-19,48633	-36,7836	-49,34849	2,743253394	0,23131517	-0,0067917	-0,0038129
12,41483	82,19075	150,75147	199,52401	-7,13883599	1,73898742	0,84247133	0,0967431
-19,75427	-114,1358	-202,5596	-264,1428	10,75542845	-1,7382511	0,24951543	1,0314896
10,99542	52,4115	89,534123	114,86285	-5,4625843	0,77949921	-0,0861277	-0,1252767
C1(4*4)T1=8				C2(4*4)T1=8
-5,136108	-31,15906	-56,49719	-74,47357	1,91441250	0,10152187	-0,01243125	0,00310781
22,66113	126,2549	223,37402	291,03369	-3,30330000	1,57657500	0,45045000	-0,05899
-33,7533	-168,7665	-290,462	-373,6972	4,57211250	-1,14302812	0,76201875	0,89809353
17,22656	74,64844	124,52344	158,02734	-2,21760000	0,47040000	-0,20160000	0,15840000
C1(4*4)T1=9				C2(4*4)T1=9
-8,750445	-46,66904	-82,14703	-106,8626	1,372594731	0,03373505	-0,0074754	0,0052574
36,95168	183,2188	315,67296	406,46853	-1,19913254	1,29675777	0,17446234	-0,0820999
-52,42798	-237,6735	-399,8971	-509,3004	1,525097942	-0,5247649	0,98840658	0,53158
25,22461	102,0996	167,30609	210,58045	-0,70765555	0,19606041	-0,1562356	0,5461683
C1(4*4)T1=10				C2(4*4)T1=10
-13,70138	-66,54956	-114,5044	-147,4296	1,00000	0,00000	0,00000	0,00000
55,88352	254,679	429,96096	548,57088	0,00000	1,00000	0,00000	0,00000
-76,37058	-322,4536	-533,1798	-673,6976	0,00000	0,00000	1,00000	0,00000
35,18592	135,2982	218,65536	273,43888	0,00000	0,00000	0,00000	1,00000