Содержание отчета

1.Титульная страница: названия вуза, кафедры, дисциплины, лабораторной работы (с её порядковым номером); Ф.И.О. и группа студента, Ф.И.О. преподавателя, дата.

2.Краткое описание алгоритма минимизации функции многих переменных.

3.Результаты поиска минимума функции многих переменных при отсутствии и наличии сбойных результатов.

4.Кратко изложить реализацию методов: координатного спуска в методе Гаусса-Зейделя, наискорейшего спуска.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сведение задачи поиска решения нелинейных уравнений к задаче минимизации многомерных функций

2.Минимизация функции многих переменных при наличии линейных ограничений.

3. Сокращение интервала неопределенности методом золотого сечения

4.Сокращение интервала неопределенности методом квадратичной аппроксимации.

5.Изменения в блок-схеме алгоритма метода ДФП при поиске глобального минимума и наличии сбойных результатов.

Литература

1.Вычислительная математика: методические указания к лабораторным работам/Рязан.гос.радиотехн.ун-т; сост. А.Н. Кабанов, Рязань,2008.-48 с.

2.Метод псевдообращения в задачах управления: Методические указания к лабораторной работе. Сост. А.Н. Кабанов. Рязань,1997.-16c.

3.Исследование вычислительных алгоритмов: Методические указания к лабораторной работе. Сост. А.Н. Кабанов. Рязань,1998.-20c.

4. Вычислительная математика: методические указания к лабораторным работам/Рязан.гос.радиотехн.ун-т;сост.Ю.И.Малинин,Рязань,2008.-48 с.

ЛАБОРАТОРНАЯ РАБОТА №4

МЕТОДЫ АППРОКСИМАЦИИ ФУНКЦИЙ

(объем часов - 2)

Цель работы: Исследование методов аппроксимации функций на основе быстрого преобразования Фурье (БПФ) , быстрого преобразования Уолша (БПУ), быстрого преобразования Хаара (БПХ).

В результате выполнения лабораторной работы студент:

должен знать матричное представление БПФ,БПУ,БПХ

должен иметь представление о принципах выбора базисных функций.

должен уметь составлять блок-схемы алгоритмов БПФ,БПУ,БПХ.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

4.1. Быстрое преобразование Фурье

Матрица дискретного преобразования Фурье имеет вид:

где

.

Коэффициенты разложения сигнала имеют вид: .

Применяя обратное преобразование Фурье, получаем аппроксимированное представление сигнала гдеB_(m,l)=W^-lm.

Для сокращения числа операций целесообразно применять БПФ, представленный в матричной форме. Матрица преобразований имеет вид

, (1)

где I_n- единичная матрица размером (nn),A_j=A₁A₂…A_n – кронекеровское произведение,A_i=A₁A₂…A_n– прямая сумма.

,

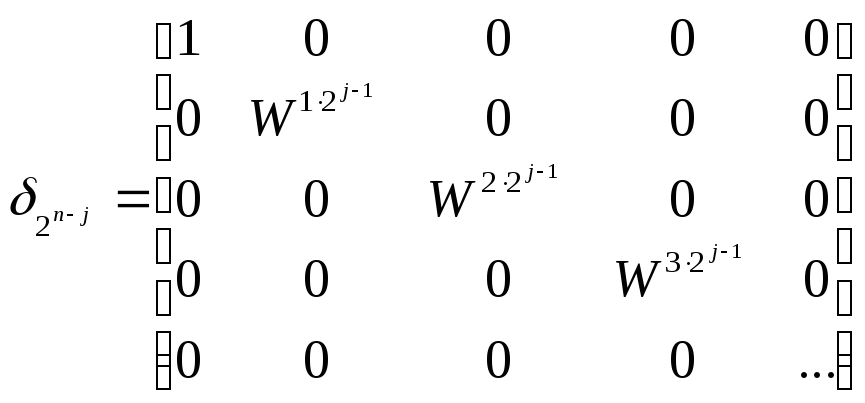где ,N= 2ⁿ– число отсчетов.

На основе формулы (1) для n= 4 получаем спектр:

(2)

где ; .

i= 2,4,6,8j= 1,3,5,7

Результаты представлены FKPс двоично-инверсными номерами.

Пример представления спектра с двоично-инверсными номерами дан в таблице 1.

Таблица 1

Номер	Двоичное представление	Двоичная инверсия (считывание в обратном порядке)	Двоично-инверсный номер
0	0 0	0 0	0
1	0 1	1 0	2
2	1 0	0 1	1
3	1 1	1 1	3