Просмотр участков двумерных графиков

Некоторые графики представляют собой достаточно сложные кривые, особый интерес в которых представляют некоторые участки. Чтобы подробнее просмотреть такие участки, можно воспользоваться контекстным меню графиков. Контекстное меню вызывается нажатием правой клавиши мыши на области графика.

Команда Zoom (масштаб) контекстного меню позволяет увеличить любой участок графика.

Чтобы воспользоваться этой командой, надо выделить некоторый график и выбрать команду Zoom из контекстного меню (рисунок 9).

Теперь перемещение мыши с нажатой левой кнопкой приводит к появлению на графике прямоугольника из пунктирных линий. Этим прямоугольником и надо отметить область просмотра графика. При этом в окне просмотра отображаются минимальные и максимальные значения XиY, определяющие область просмотра.

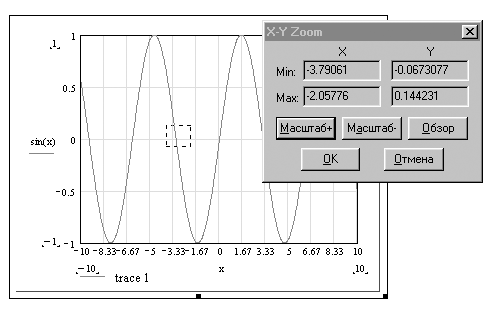
Рис. 9. Просмотр участка двумерного графика

На рисунке 10 показан результат, получаемый после нажатия кнопки "Масштаб +".

Рис. 10. Участок графика после увеличения масштаба

Порядок выполнения работы

1. Изучите теоретический материал.

2. Выполните задание, вариант которого соответствует номеру вашей бригады.

Варианты заданий

Вариант 1

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 2

1. Вычислите

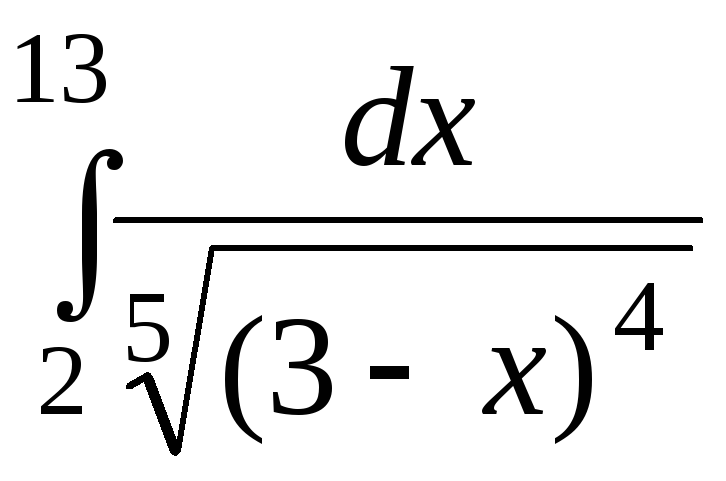
2. Постройте график функции

3. Решите графически уравнение

Вариант 3

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 4

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

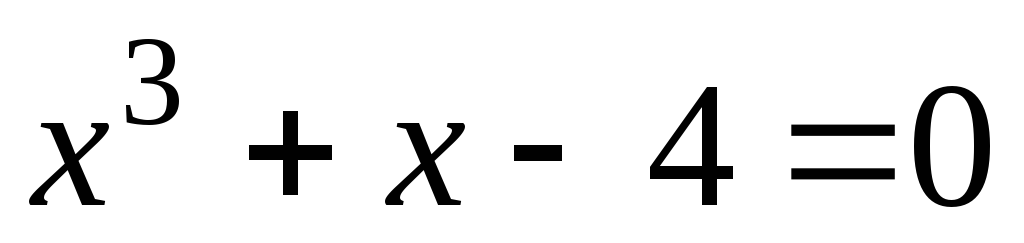
Вариант 5

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 6

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 7

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 8

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 9

1. Вычислите

2. Постройте график функции

Вариант 10

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 11

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Вариант 12

1. Вычислите

2. Постройте график функции

3. Решите графически уравнение

Контрольные вопросы

1. Какие типы блоков могут присутствовать в документе Mathcad?

2. В какой последовательности выполняются выражения в документе?

3. Как могут вводиться функции в документ Mathcad?

4. Что такое шаблоны операций и функцийи как ими пользоваться?

5. Как построить график функции одной переменной?

6. Как в одной координатной сетке построить графики нескольких функций?

7. Как осуществляется форматирование графика функции одной переменной?

8. Как просмотреть увеличенный фрагмент графика функции?

Библиографический список

1. Дьяконов В.П. Mathcad8/2000 : Специальный справочник - СПб.: Питер, 2001. - 592 с.

2. Дьяконов В.П. Mathcad2001 : Специальный справочник - СПб.: Питер, 2002. - 832 с.

3. Иванов В.В. Методы вычислений на ЭВМ : Справочное пособие - Киев, Наука, 1986. - 584 с.

4. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для вузов - М.: Наука, 1973. - 720 с.

5. Берман Г.Н. Сборник задач по курсу математического анализа –М.: Наука, 1972. – 416 с.

Лабораторная работа № 9

ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ НА ЭВМ

Цель работы: изучение влияния различных видов погрешностей на результаты вычислений на ЭВМ; разработка программ на языке высокого уровня для учета различных видов погрешностей.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. Источники и виды погрешностей результата вычислительной задачи

При решении задачи на ЭВМ практически невозможно получить точное решение. Получаемое численное решение почти всегда содержит погрешность, т.е. является приближенным. Погрешности решения задач на ЭВМ объясняются следующими причинами:

1) математическая модель задачи является приближенным описанием реального объекта или процесса. Поэтому получаемые результаты также всегда будут приближенными, а их погрешности зависят от степени адекватности моделей реальному объекту или процессу;

2) исходные данные при решении вычислительной задачи, как правило, содержат погрешности. Это объясняется тем, что исходные данные получают в результате экспериментов, наблюдений, измерений или в результате решения вспомогательных задач;

3) применяемые для решения вычислительных задач методы в большинстве случаев являются приближенными, так как получить аналитическое решение задачи обычно не удается;

4) использование ЭВМ вносит ошибки, которые появляются при вводе-выводе данных в процессе вычислений.

С учетом указанных выше причин погрешность решения вычислительной задачи на ЭВМ складывается из трех составляющих:

- неустранимая погрешность;

- погрешность метода;

- вычислительная погрешность.

Неустранимая погрешность соответствует первым двум причинам и единственный способ уменьшить эту погрешность заключается в переходе к более точной модели или в использовании более точных входных данных.

Погрешность метода определяется третьей причиной, причем появление этой погрешности практически неизбежно при любых вычислениях.

Вычислительная погрешность возникает в основном из-за округления чисел при вводе-выводе, а также при выполнении арифметических операций в ЭВМ. Это обусловлено ограниченной разрядностью ЭВМ и особенностями представления данных в памяти машины.