
- •Методические указания к лабораторным работам по дисциплине "Вычислительная математика "
- •Лабораторная работа №1
- •(Количество часов -2 час. )
- •Определение псевдообратной матрицы для произвольной матрицына основе метода ортогонализации Грамма-Шмидта (гшо)
- •Построение псевдообратной матрицы на основе метода ортогонализации Грамма-Шмидта.
- •1.1. Сокращение интервала неопределенности методом золотого сечения
- •1.2. Сокращение интервала неопределенности методом квадратичной аппроксимации
- •1.3. Минимизация многомерной функции при наличии линейных ограничений на основе метода Давидона-Флетчера-Пауэлла
- •Порядок выполнения работы
- •2. Учебный пример выполнения лабораторной работы
- •2.1. Минимизация многомерных функций
- •Содержание отчета
- •4.2. Быстрое преобразование Уолша
- •4.3. Быстрое преобразование Хаара
- •Порядок выполнения работы
- •Порядок выполнения работы
- •3. Метод Рунге-Кутта 4-го порядка
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Построение графика функции одного аргумента
- •Просмотр участков двумерных графиков
- •Порядок выполнения работы
- •1.2. Абсолютные и относительные погрешности
- •1.5. Погрешности произведения и частного приближенных чисел
- •3. Содержание отчета по лабораторной работе
- •Контрольные вопросы
- •Лабораторная работа № 10 решение нелинейных уравнений
- •1. Теоретическая часть
- •1.1. Метод половинного деления
- •1.2. Метод хорд
- •1.3. Метод Ньютона (касательных)
- •1.4. Метод простой итерации
- •2. Порядок выполнения работы
- •3. Содержание отчета по лабораторной работе
- •4. Контрольные вопросы
- •5. Исходные данные
- •Интерполирование функций
- •1. Теоретическая часть
- •1.1. Формула Лагранжа
- •1.2. Интерполирование по схеме Эйткена
- •1.4. Формула Ньютона с разделенными разностями
- •Интерполяционный многочлен Ньютона, использующий разделенные разности, имеет вид:
- •1.6. Интерполяция сплайнами
- •2. Порядок выполнения работы
- •3. Содержание отчета по лабораторной работе
- •4. Контрольные вопросы
- •5. Исходные данные
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Вечерний факультет
Кафедра дистанционных образовательных технологий
Кафедра автоматизированных систем управления
Методические указания к лабораторным работам по дисциплине "Вычислительная математика "
Направление подготовки – 230400_62 «Информационные системы и технологии»
Квалификация выпускника – бакалавр
Форма обучения –заочная
Рязань 2013 г.
Пояснительная записка
Работы проводятся на факультете ”Автоматики и информационной технологии в управлении ” для направления подготовки – 230400_62 «Информационные системы и технологии» .
Общий объем занятий 28 часов.
Целью данных лабораторных работ является обучение студентов
- реализации важнейших вычислительных алгоритмов с помощью современных математических программных систем,
- практическим методам анализа важнейших вычислительных алгоритмов математических вычислений, реализуемых на ЭВМ.
С учетом важности знаний по оперативным методам обработки
лабораторные работы предусматривают исследование ряда методов повышения оперативности реализации вычислительных алгоритмов.
Форма проведения работ – сочетание обучения на демонстрационных примерах и выполнения контрольных заданий.
Форма текущего контроля выполнения - проверка результатов выполнения демонстрационных и контрольных примеров.
Форма итогового контроля выполнения - проверка отчета и собеседование.
Лабораторная работа №1
Математические методы повышения устойчивости решения СЛАУ.Метод ортогонализации Грамма-Шмидта.
(Количество часов -2 час. )
Цель работы: Теоретическое и практическое освоение с помощью ПЭВМ
алгоритма устойчивого решения систем линейных уравнений методом ортогонализации Грамма-Шмидта.
В результате выполнения лабораторной работы студент:
должен знать метод реализации алгоритма ,
должен иметь представление о реализации метода с помощью
пакета EXCEL.
должен уметь проверить достоверность решения.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Определение псевдообратной матрицы для произвольной матрицына основе метода ортогонализации Грамма-Шмидта (гшо)
Столбцы матрицы
 ,
которые обозначим
,
которые обозначим ,
преобразуются методом ГШО в ортогональные
векторы (не обязательно, чтобы они
получились ортонормированными). Из
множества этих векторов образуется
матрица
,
преобразуются методом ГШО в ортогональные
векторы (не обязательно, чтобы они
получились ортонормированными). Из
множества этих векторов образуется
матрица .
.
Ортогонализация столбцов
матрицы методом ГШО производится по
уравнениям
![]() ;
;
 , (10)
, (10)
где
![]() .
.
Здесь
![]() - норма вектора, определяемая выражением
- норма вектора, определяемая выражением![]() .
.
Сравнивая нормы векторов
![]() ,
принимают решение об обнулении вектора
с малой нормой.
,
принимают решение об обнулении вектора
с малой нормой.
Столбцы
 матрицы
матрицы переставляются с помощью матрицы
перестановок
переставляются с помощью матрицы
перестановок таким образом, что
таким образом, что
![]() , (11)
, (11)
где

Матрица перестановок
![]() может быть подобрана следующим образом.
Если требуется поменять местамиi
– столбец и j
– столбец, то в единичной
может быть подобрана следующим образом.
Если требуется поменять местамиi
– столбец и j
– столбец, то в единичной
![]() - матрице
- матрице![]() нужно сделать следующие замены:
нужно сделать следующие замены:![]() ;
;![]() .
В общем случае матрица
.
В общем случае матрица![]() может включать произведение нескольких
перестановочных матриц.
может включать произведение нескольких
перестановочных матриц.
Столбцы
 исходной матрицы
исходной матрицы переставляются с помощью матрицы
перестановок
переставляются с помощью матрицы
перестановок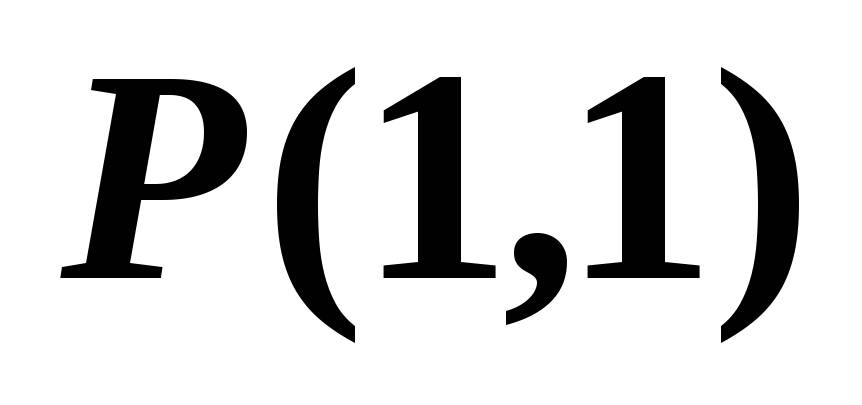 ,
применяемой в п.2. При этом получают
новую матрицу со столбцами, которые
обозначим, например, так:
,
применяемой в п.2. При этом получают
новую матрицу со столбцами, которые
обозначим, например, так:
![]() ;
;
![]() .
.
Вычисляются вспомогательные коэффициенты

Вычисляется матрица
 размером
размером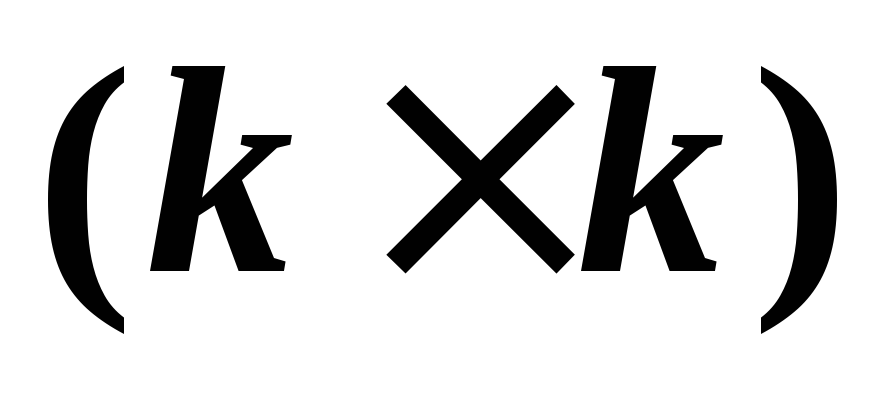 с элементами
с элементами
![]() .
.
Вычисляется матрица
 размером
размером с элементами
с элементами

Вспомогательная матрица
 находится методом ГШО из столбцов
матрицы
находится методом ГШО из столбцов
матрицы ,
т.е. к столбцам матрицы, сформированной
из двух матриц
,
т.е. к столбцам матрицы, сформированной
из двух матриц
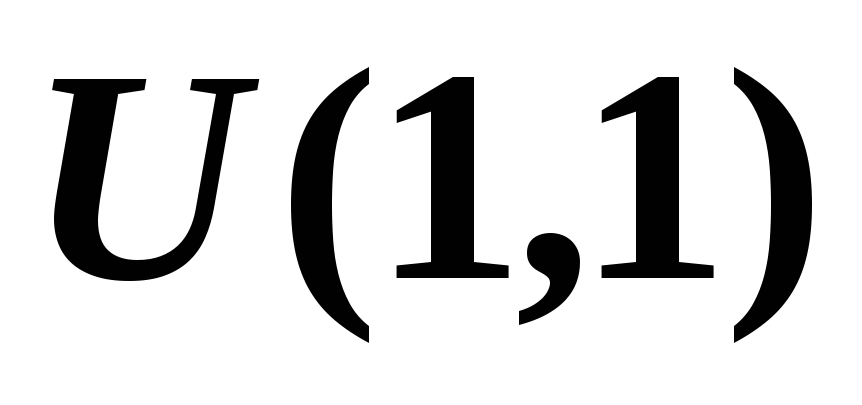 ,
,
 ,
применяют процедуру, аналогичную
процедуре (10), но с тем
отличием, что после получения каждого
ортогонального вектора, начиная с
первого вектора, его нормируют путем
деления всех компонентов вектора на
его норму. Условно эту процедуру можно
представить в виде следующей цепочки
преобразований:
,
применяют процедуру, аналогичную
процедуре (10), но с тем
отличием, что после получения каждого
ортогонального вектора, начиная с
первого вектора, его нормируют путем
деления всех компонентов вектора на
его норму. Условно эту процедуру можно
представить в виде следующей цепочки
преобразований:
 .
.
Здесь размер матриц
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Вычисляется матрица
 .
.Используя матрицу, полученную в (11), вычисляем матрицу
![]() .
.
С помощью вспомогательных матриц
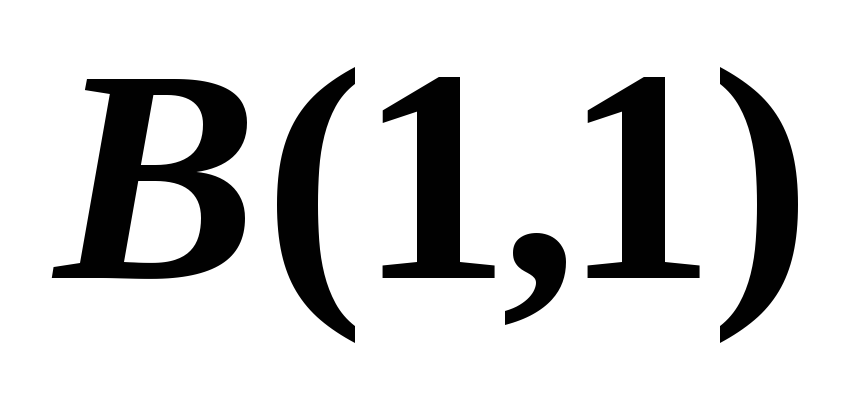 ,
, ,
, ,
, ,
, ,
вычисленных в пп. 2, 5, 6, 8, 9, определяется
псевдообратная матрица
,
вычисленных в пп. 2, 5, 6, 8, 9, определяется
псевдообратная матрица
![]() .
.
Оценка коэффициентов линейной регрессии
определяется выражением
![]() .
.
Пример 1.Получение устойчивого решения системы линейных уравнений на основе использования псевдообратных матриц.
Система уравнений имеет вид

Её точное решение:
![]()
Рассмотрим систему с измененной правой частью:
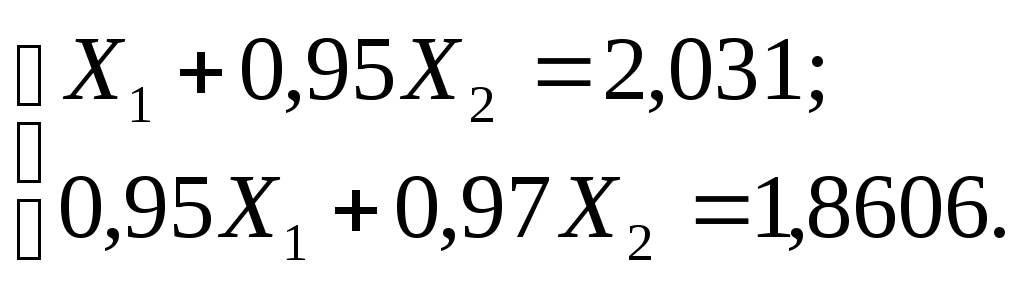
Её точное решение:
![]() ,
т.е. решение неустойчиво.
,
т.е. решение неустойчиво.
Как и ранее, исследуем матрицу системы
на обусловленность. Матрица
![]() в данном случае симметрична. Тогда на
основании того, что
в данном случае симметрична. Тогда на
основании того, что
![]() ,
имеем
,
имеем
![]()
Обусловленность матрицы
![]() ,
т.е. матрица системы плохо обусловлена
и необходимо применять методы повышения
устойчивости решения. Рассмотрим этот
метода.
,
т.е. матрица системы плохо обусловлена
и необходимо применять методы повышения
устойчивости решения. Рассмотрим этот
метода.
