
- •Элементы интерактивной компьютерной графики
- •Класс 2: двухуровневые или представляемые в нескольких «цветах» изображения
- •Структура графического изображения
- •Блок-схема графической системы
- •Методы кодирования графической информации
- •Позиционные методы кодирования ги. Рецепторный метод кодирования
- •Метод тетрарного дерева
- •Структурные методы кодирования Цепной метод кодирования
- •Кусочно – линейная аппроксимация контура изображения
- •Аппроксимация группы точек окружностью
- •Аналитические методы кодирования
- •Методы структурно – символического кодирования
- •Типичная система команд дисплейного процессора
- •Форматы дисплейных команд
- •А) Команды, управляющие лучом гд.
- •Геометрические преобразования
- •Двумерные преобразования Перенос (сдвиг)
- •Масштабирование
- •Поворот изображения
- •Однородные координаты и матричное представление двумерных преобразований
- •Композиция двумерных преобразований
- •Вопросы эффективности
- •Матричное представление трехмерных преобразований
- •Видовая операция (отсечение части изображения по прямоугольному окну)
- •Высокопроизводительные графические преобразования
- •Алгоритмы растровой графики
- •Алгоритм Брезенхэма для отрезков прямых
- •Растровая развертка окружностей
- •Алгоритм брезенхема для генерации окружности
- •Типы графических дисплеев Векторный дисплей
- •Организация памяти в растровых графических дисплеях
- •Организация дисплейного файла
Видовая операция (отсечение части изображения по прямоугольному окну)
Процессы 2 и 3 в канале вывода (рис. 4.2) служат для преобразования независимого от устройства описания объекта в дисплейную программу конкретного устройства, которая генерирует изображение, являющееся частным видом объекта. На рис. 4.3 более подробно показаны три шага, выполняемые этими двумя процессами:
Мировые коорд. Нормиров. коорд. Физич. коорд.
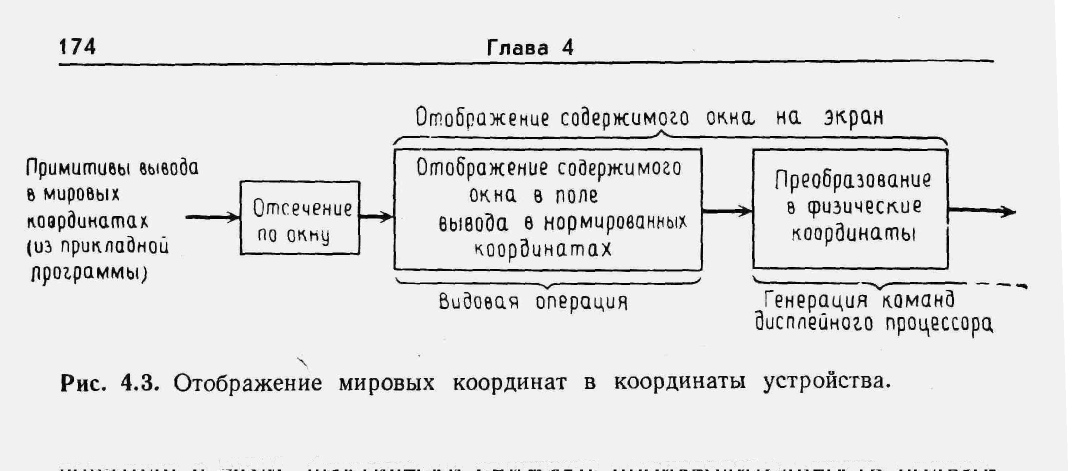
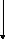
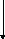
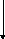
- отсечение,
- отображение окна в поле вывода
- и генерация дисплейных команд в физические координаты экрана конкретного устройства.
Первые два шага обычно считаются частью видовой операции, в то время как третий входит в процесс генерации команд ДП. (Видовая операция также может преобразовать примитивы непосредственно в физические координаты).
В этом разделе рассмотрены первые два шага: отсечение и преобразование «окно — поле вывода», которое отображает оставшиеся после отсечения примитивы, заданные в мировых координатах, в примитивы, заданные в нормированных координатах.
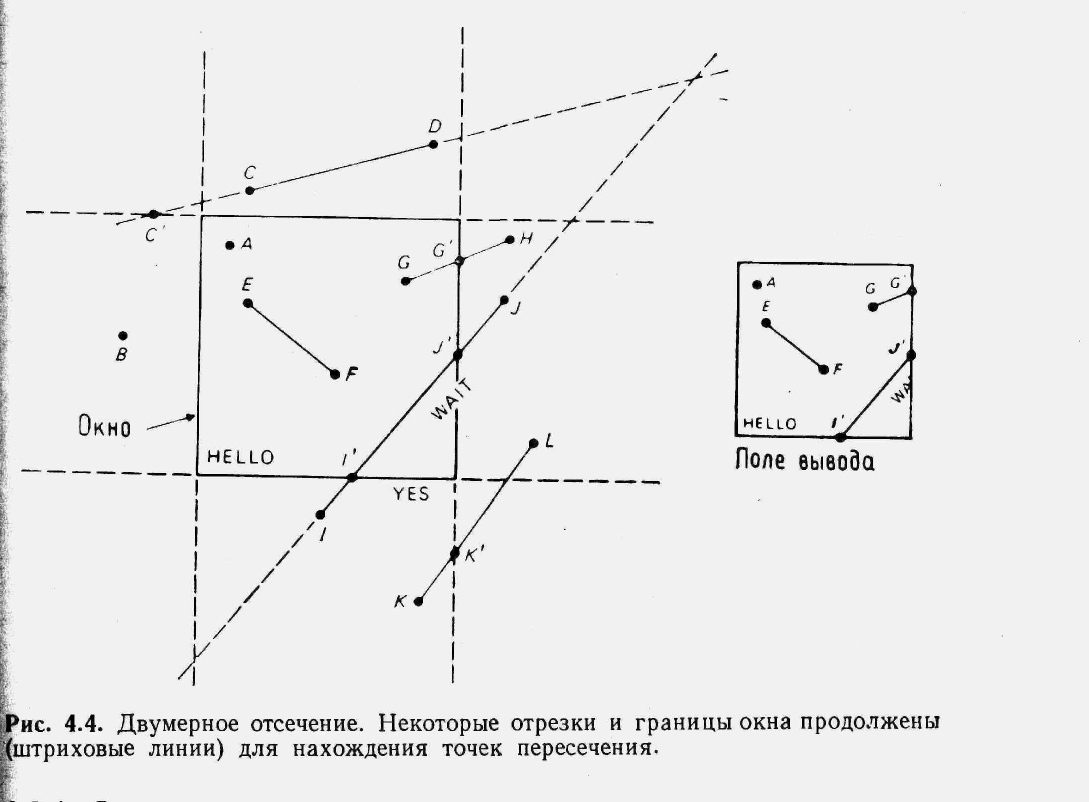
Шаг 1. Отсечение примитивов вывода
Рис. 4.4 иллюстрирует операцию отсечения точек, линий и цепочек литер для типичного вертикального прямоугольного окна.
Точка А находится внутри окна и поэтому она изображается внутри юля вывода на видовой поверхности. Точка В находится вне окна поэтому она не изображается. Отрезок прямой EF изображается полностью, отрезки GH и IJ изображаются частично (отсекаются), CD и KL не изображаются совсем. Текстовая строка YES не изображается, строка HELLO изображается, а строка WAIT отсекается, а затем изображается. Работа с текстом (поворот и отсечение) показана здесь на уровне отдельных литер.
Отметим, что отрезки, пересекающие прямоугольное окно (или любой выпуклый многоугольник), в результате отсечения всегда превращаются в один отрезок, такой, как I' J' часть I J. Точки и отрезки, находящиеся на границе окна, считаются внутренними и как следствие изображаются.
Сначала мы рассмотрим отсечение точек и отрезков прямых, |а затем отсечение текста.
Точки. Отсечение точек осуществляется довольно просто. Если
xmin и xmах - x - координаты границ окна, а ymin и ymax — y - координаты, то, для того чтобы точка (х, у) была видимой, должны удовлетворяться четыре неравенства:
xmin ≤ x ≤ xmax, ymin ≤ y ≤ymax
Если хотя бы одно из этих неравенств неверно, точка в окне не изображается.
Отрезки. Отсечение отрезков прямых в общем случае требует большего числа проверок и вычислений, чем отсечение точек. К счастью, достаточно рассмотреть только конечные точки отрезка, не принимая во внимание бесконечное множество внутренних точек.
Прежде всего, можно быстро разобраться с классом отрезков (примером является отрезок EF на рис. 4.4), обе конечные точки которых лежат внутри окна. Такие отрезки целиком находятся внутри прямоугольного окна и, следовательно, могут быть приняты целиком.
Отрезки, одна конечная точка которых находится внутри окна, а другая вне его, требуют операции отсечения (отрезок GH на рис. 4.4).
Отрезки, обе конечные точки которых находятся вне окна, необходимо проверить по границам окна, чтобы выявить возможное пересечение с окном; при обнаружении пересечения необходимо отсечение. (На рис. 4.4 отрезки CD и K.L не попадают в окно, в то время как IJ должен отсекаться.)
Один из очевидных способов отсечения отрезков, которые нельзя принять целиком, состоит в определении точек пересечения прямой, содержащей отрезок, с каждой из четырех прямых, на которых лежат границы окна, и проверки, не лежит ли хотя бы одна точка пересечения на границе; если лежит, то отрезок частично находится в окне. Таким образом, для каждого отрезка и для каждой стороны окна необходимо взять две математически бесконечные прямые линии, содержащие их, и найти точку пересечения. Затем необходимо проверить, не является ли точка пересечения внутренней, т. е. лежащей одновременно и на отрезке, и на стороне окна. Если да, то имеет место пересечение отрезка с окном (на рис. 4.4 точки I' и G' — внутренние точки, а С' и К' - нет).
К сожалению, при таком подходе для каждой пары (сторона — отрезок) необходимо решать систему двух уравнений, используя операции умножения и деления. Реализация простого графического пакета
Эффективность операции отсечения приобретает особое значение интерактивной графике, поскольку типичное изображение состоит из сотен или даже тысяч отрезков, которые должны обрабатываться с максимально возможной скоростью, если требуется обеспечить плавный переход от одного вида объекта к следующему. Болee эффективный алгоритм мог бы произвести сначала некоторые дополнительные проверки, чтобы выяснить, действительно ли необходимы вычисления для нахождения точки пересечения. Во-первых, можно проверить, не находятся ли обе конечные точки отрезка в окне; в этом случае отрезок принимается целиком. Во-вторых, можно было бы проверить, в какой области находится отрезок. Например, два простых сравнения координат у показывают, что обе конечные точки отрезка CD на рис. 4.4 имеют координату у, большую ymах. Это означает, что отрезок CD находится выше окна и его можно отбросить целиком. Аналогичным образом можно отвергнуть целиком отрезки, обе конечные точки которых находятся ниже ymin, левее xmin или правее xmах.
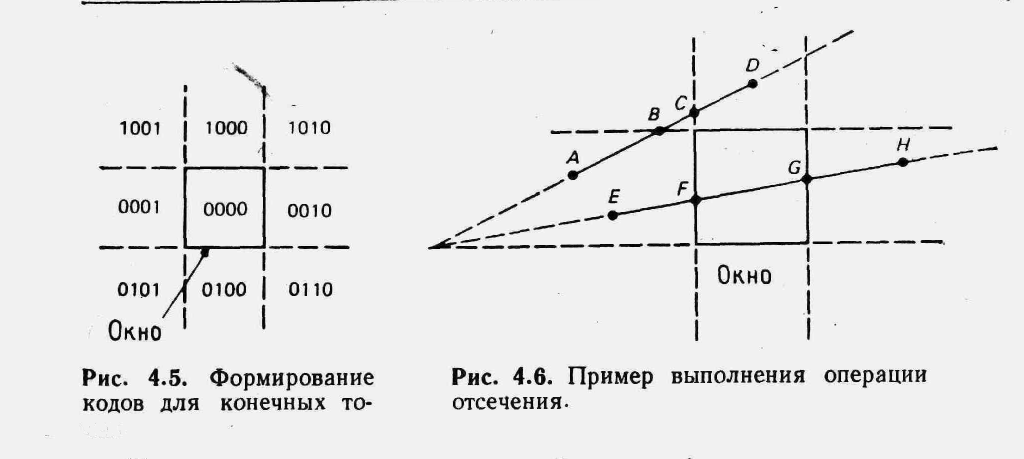
Алгоритм отсечения Коэна — Сазерленда. Алгоритм отсечения Коэна — Сазерленда позволяет быстро выявить отрезки, которые могут быть отвергнуты или приняты целиком; при этом используются проверки области расположения отрезков. Вычисления для определения точки пересечения требуются в тех случаях, когда отрезки не попадают ни в один из этих классов. Этот алгоритм особенно эффективен в двух крайних случаях: 1) большое окно, содержащее большинство примитивов; 2) относительно маленькое окно и обширное, насыщенное изображение, в котором большинство примитивов лежит вне окна. В обоих случаях большинство отрезков |можно принять или отбросить целиком.
Работа алгоритма начинается с приписывания конечным точкам отрезков 4-битового кода «вне/внутри» по правилу, иллюстрируемому рис. 4.5. Каждому биту присваивается значение 1 (истина), и выполняется соответствующее данному биту условие, характеризующее взаимное расположение точки и окна (биты нумеруются слева направо): бит 1 — точка выше окна; бит 2 — точка ниже окна; бит 3 — точка справа от окна; бит 4 — точка слева от окна. В противном случае биту присваивается значение 0 (ложь).
Для языков, позволяющих работать с битами, существует особенно эффективный способ вычисления этого кода, вытекающий из того факта, что:
бит 1 является знаковым битом разности (ymах — у),
бит 2 — знаковым битом для (у — уmin),
бит 3 — для (хmax — х),
бит 4 — для (х — хmin).
Точка находится внутри окна (код «вне/внутри» равен 0000), если все эти разности неотрицательны.
Отрезок можно принять целиком, если оба его конца находятся внутри окна (оба кода 0000). Отрезок отбрасывается без вычислений, если оба его конца находятся выше, ниже, левее или правее окна. В этих случаях соответствующие биты в обоих кодах равняются 1, и это легко выявить, применив к кодам логическую операцию И, и проверив результат на отличие от 0000.
Если результат логической операции И равняется 0000, отрезок нельзя ни принять, ни отбросить целиком, так как он может пересекаться с окном. (На рис. 4.6 отрезки AD и ЕН попадают в этот класс, но только отрезок ЕН действительно пересекается с окном.)
Для определения пересечения в алгоритме не используется очевидный метод проверки на параллельность, решение системы двух уравнений и проверка, не является ли точка пересечения внутренней для обоих отрезков. Вместо него применяется итеративная стратегия «разделяй и властвуй», требующая небольшого объема вычислений. В этом случае используется горизонтальность либо вертикальность сторон окна, что дает возможность определить координату х или у точки пересечения без вычислений. Кроме того, используется тот факт, что часть отрезка, находящаяся с внешней стороны от границы окна, может быть отброшена. Оставшийся отрезок проверяется на возможность его принятия или отбрасывания целиком. Если это невозможно, процесс повторяется для другой стороны окна. На каждой итерации конечная точка отрезка с ненулевым кодом «вне/внутри» заменяется на точку, лежащую на стороне окна или на прямой, содержащей сторону.
Порядок перебора сторон окна абсолютно произволен: независимо от порядка отсечение некоторых отрезков потребует четырех итераций, определяющих пересечения со всеми четырьмя сторонами окнa.
Примем порядок, соответствующий расположению битов в коде:
I. верхняя часть — отбросить часть отрезка, расположенную окном;
2. нижняя часть — отбросить часть отрезка, расположенную окном;
3. правая сторона — отбросить часть отрезка, расположенную справа;
4. левая сторона — отбросить часть отрезка, расположенную слева.
В качестве примера рассмотрим два отрезка прямых, приведенных на рис. 4,6, и разделим их на части. Для отрезка DA итерационная последовательность была бы следующей:
1. Проверка кодов для А и D и результата применения к ним операции И; нельзя принять или отбросить целиком.
2. Вычисление точки пересечения В; ВА — новый отрезок, отбрасывается, поскольку находится над окном.
3. Проверка кодов для А и В; отрезок отбрасывается целиком.
Для отрезка ЕН последовательность немного длиннее:
1. Проверка кодов для Е, Н; нельзя принять или отбросить целиком.
2. Вычисление точки пересечения G; отбрасывание отрезка GH.
3. Проверка для отрезка EG;, нельзя принять или отбросить целиком.
4. Вычисление точки пересечения F; отбрасывание отрезка EF.
5. Проверка для отрезка FG; принимается целиком.
Шаг 2. Отображение окна на поле вывода.
После отсечения примитива по границам окна процессор видовой операции отображает его на поле вывода.
Точка (Xm Ym) отображается в точку (Xf Yf) с сохранением пропорций, т.е. с сохранением ее относительного положения внутри замкнутого прямоугольника.
Более точно это условие формулируется следующим образом:
Отношение расстояния о Y- границы к длине X- границы и отношение расстояния от Х- границы к длине Y –границы должны быть одинаковы для окна и поля вывода.
Это условие запишем следующим образом:
![]() =
=
![]()
![]()
![]() =
=
![]()
Отсюда можно вывести уравнения отображения
Xf
= Xf
min
+ (![]() )
* (Xm
– Xm
min)
)
* (Xm
– Xm
min)
Yf
=
Yf
min
+ (![]() )
* (Ym
– Ym
min)
)
* (Ym
– Ym
min)
Или
Xf = Sx * (Xm – Xm min) + Xf min,
Yf = Sy * (Ym – Ym min) + Yf min
Здесь – Sx и Sy – параметры масштабирования, согласующие размеры окна и поля вывода, Xf min и Yf min – параметры переноса, привязывающие промасштабированные (относительные) координаты окна (Xm – Xm min, Ym – Ym min) к левому нижнему углу поля вывода.
Эти уравнения можно упростить и записать в следующем виде:
Xf = Sx * Xm + a, Yf = Sy * Ym + b,
где для каждой координаты имеется одно умножение на заранее известный коэффициент и одно сложение с заранее известным числом.
Как показывают предыдущие рассуждения по преобразованию графического изображения, использование однородных координат позволяет объединить целый комплекс преобразований в один программный модуль (подпрограмму) на вход которого будут вводиться значения координат точки двух (трех)-мерного пространства и 10 параметров (для трехмерного пространства), определяющих преобразование.
Выходными параметрами являются значения координат Xp и Yp перспективной проекции точки.
Sx Sy Sz Xm Ym Zm Z0
 X
X
Вычисление компонент матрицы 4 х 4
Выполнение операций умножения на
матрицу
Деление первых двух компонент
результирующего вектора на четвертую
компоненту
В Х О Д
Х О Д
Y В Ы Х О Д

Yp
 Z
Z

Три угла поворота , , .
Три масштабирующих множителя Sx, Sy, Sz.
Три параметра переноса Xm, Ym, Zm
Параметр Z0, определяющий центр перспективного преобразования.
При наличии такого программного модуля преобразования производятся достаточно быстро для того, чтобы выполняться в реальном времени.
Подтверждением тому является содержание следующего параграфа.
