Курс_лекций_по_теории_случайных_процессов

72 Глава 3. Цепи Маркова

Для доказательства второго утверждения единственности инвариантного распределения,

k=0

Заметим, что предельный переход в соотношениях (10.10, 10.11) под знаком матричного умножения возможен в силу конечности пространства состояний и, следовательно, равномерной сходимости.

Приведенная теорема позволяет привести содержательную трактовку среднего числа посещений knkj некоторого состояния j без захода в другое k, введенной в разделе 10.2. формулой (10.6).

Доказательство. Покажем, что предельное выражение в теореме 10.5 не зависит от выбора состояния e. Фиксируя другое запрещенное состояние, скажем k, найдем

(n) knkj

lim pij = m ;

n!1 kk

откуда в силу единственности предела имеем

10.4.Эргодические теоремы

По ЗБЧ частота hn(A) появления события A в последовательности независимых испытаний сходится к его вероятности по вероятности (и с вероятностью 1 в случае применимости УЗБЧ)

Аналогичные утверждения справедливы также для сумм Sn = Xk н.о.р. с.в. Xn. Именно,

Эргодическими теоремами в теории случайных процессов называются теоремы о сходимости средних по времени функционалов от траекторий с.п. к средним по инвариантной вероятностной мере в фазовом пространстве. Частным случаем эргодических теорем являются законы больших чисел для независимых слагаемых. Обобщение этих законов на случай более общих процессов и называется эргодическими теоремами. В зависимости от вида сходимости (также как и в законах больших чисел) можно говорить о слабой (относительно сходимости по вероятности), сильной (относительно сходимости с вероятностью 1) или среднеквадратической эргодических теоремах

в соответствии с выбранным видом сходимости. В настоящем разделе с помощью обычного и усиленного закона больших чисел для сумм независимых слагаемых будут одновременно доказаны слабая и сильная эргодические теоремы для эргодической марковской цепи.

Пусть X = fXn; n = 0; 1; g конечная неразложимая эргодическая марковская цепь. Различные вероятностные и стоимостные характеристики цепи выражаются в виде функционалов от их траекторий вида

1 k n

где функции f(i) и g(i; j) представляют собой “плату” за посещение цепью состояния i и за переход из состояния i в состояние j. Выбирая эти функции специальным образом можно получить различные вероятностные или стоимостные характеристики цепи. Например, для индикаторной функции некоторого состояния j или множества состояний A; f(X(s)) = 1A(X(s)) функционал (10.12) представляет собой время, проведенное цепью в этом множестве состояний, а величина

равна доле времени пребывания в нем. Если c(i) штраф за пребывание в состоянии i, и

X

f(Xk) = c(j)1j(Xk);

j2E

то функционал (10.12) описывает штраф от работы системы за n шагов, а величина (10.14) средние издержки в единицу времени. Аналогичным образом используется функционал типа (10.13) (примеры см. ниже). Поэтому во многих практических задачах представляет интерес исследование асимптотического поведения средних значений функционалов (10.12, 10.13) по времени.

Теорема 10.7 (Эргодическая, или ЗБЧ). Для неразложимой конечной (эргодической) марковской цепи X с инвариантным распределением имеют место почти наверное (и по верорятности) предельные соотношения

Доказательство. Идея доказательства состоит в представлении функционала в виде суммы независимых слагаемых. С этой целью фиксируем некоторое состояние, скажем e, обозначим через Sn Sn(e) моменты последовательных посещений этого состояния, а через Nn Nn(e) число его посещений за n шагов процесса и представим функционал (10.12) в виде суммы по моментам последовательных посещений цепью выбранного состояния.

XX

Поскольку состояние e фиксировано, а в силу марковского свойства поведение цепи в будущем при известном настоящем не зависит от прошлого, то величины Yk независимы и одинаково распределены, кроме, быть может, первой и последней. В силу возвратности цепи велична Nn стремится к бесконечности при n ! 1 (см. закон больших чисел для процессов восстановления, раздел 5.4.). Поэтому представляя среднее по времени от функционала (10.12) в виде

замечаем, что второе слагаемое в правой части этого выражения сходится (по вероятности и с вероятностью 1) в силу обычного и усиленного законов больших чисел для процессов восстановления и сумм независимых слагаемых к величине

Оценим теперь первое и последнее слагаемые в этой сумме. В силу конечности среднего времени возвращения и ограниченности (в силу конечности фазового пространства) функции f(:) первое слагаемое ограничено в среднем. Поэтому в силу неравенства Чебышева соответствующее слагаемое сходится (по вероятности) к нулю. (Для получения соответствующего утверждения о сходимости с вероятностью 1 необходимо воспользоваться более сильным неравенством Колмогорова). Аналогично, в силу конечности в среднем остаточного времени жизни (обратного времени возвращения) для соответствующего процесса восстановления, доказывается сходимость к нулю (по вероятности и с вероятностью 1) последнего слагаемого.

Таким образом, доказано первое утверждение теоремы о сходимости соответствующего среднего по времени. Вычислим теперь его предельное значение. Очевидно, что знаменатель равен среднему времени возвращения mee в состояние e. Вычислим значение числителя. Представим функцию g(Xi) в виде

X

g(Xi) = g(j)1j(Xi):

j2E

Тогда 8k 2 E

а для последнего среднего значенния имеем по определению и в силу теоремы об инвариантных вероятностях (см раздел 10.2.)

Таким образом, подставляя полученные выражения для MeY1 и Me[S1] в формулу 10.17 получим утверждение теоремы для функционала Fn(X). Для функционала Gn(X) доказательство проводится аналогично.

Частным случаем этой теоремы, который получается из нее при f(j) = 1k(j), является обычный закон больших чисел для эргодической марковской цепи о том, что частота посещений отдельного состояния k равна его инвариантной вероятности k и обратно пропорциональна времени возвращения в него mkk.

10.5.Фундаментальная матрица эргодических цепей и ее свойства.

При исследовании эргодических цепей важную роль играет матрица Z = (I (P )) 1. Докажем, прежде всего, существование такой матрицы, т.е. обратимость матрицы I (P ).

Лемма 10.1. Для регулярной цепи Маркова матрица I (P ) обратима и справедливо представление

X

Z = (I (P )) 1 = P n :

n 0

Доказательство. Действительно, используя формулу бинома Ньютона имеем

откуда используя свойство (1) предельной матрицы (см. теорему 10.6) найдем, что для любого k < n справедливо равенство P k n k = , в силу которого последняя сумма преобразуется в

X

(P )n = P k( 1)n k n k = P n :

0 k n

Наконец, в силу сходимости P n ! аналогично следствию 9.2 к теореме 9.1 получаем утверждение.

Аналогичное утверждение справедливо для произвольной эргодической цепи, если сходимость понимать в смысле Чезаро.

Теорема 10.8. Для произвольной эргодической цепи матрица I (P ) обратима и справедливо представление

Определение 10.2. Матрица Z = (I (P )) 1 называется фундаментальной матрицей эргодической цепи.

Многие характеристики эргодических цепей выражаются через эту матрицу. Рассмотрим некоторые ее свойства.

Теорема 10.9 (Свойства фундаментальной матрицы). Фундаментальная матрица эргодической цепи обладает свойствами

76 Глава 3. Цепи Маркова

Теорема 10.10. Матрица средних времен достижения M эргодической цепи удовлетворяет уравнению

M = P (M Mdg) + I;

которое имеет единственное решение

M = (I Z + EZdg)D;

где через Adg обозначается матрица, содержащая только диагональные элементы матрицы A.

Доказательство провести самостоятельно в виде упражнения 4 (для указания см. [11]). Через фундаментальную матрицу выражаются и другие характеристики эргодической цепи,

например, матрица дисперсий времен достижения.

10.6.Дополнения

Вопросы для контроля.

1.Какая цепь называется эргодической?

2.Каково распределение времени пребывания в каком-либо множестве состояний и времени достижения какого-либо множества состояний эргодической цепи?

3.Какие формулы справедливы для времени возвращения в любое эргодическое состояние?

4.Какова частота посещений состояний эргодического класса?

5.Какое распределение называется инвариантным?

6.Что называется системой уравнений равновесия?

7.Сформулируйте теорему о сходимости переходных вероятностей для неразложимой марковской цепи?

8.Каковы свойства предельной матрицы эргодической цепи?

9.Сформулируйте эргодическую теорему.

10.Какая матрица называется фундаментальной матрицей эргодической цепи?

11.Каковы свойства фундаментальной матрицы эргодической цепи?

Упражнения.

1.Покажите, что если X эргодическая цепь, то ее сужение iX на подмножество E n fig) является обрывающейся цепью для любого i 2 E.

Указание. Действительно, достаточно показать, что существует k такое, что pki > 0, но если это не так, то в i нельзя перейти ни из какого k 6= i. Следовательно i либо поглощающее, либо несущественное, что противоречит предположению об эргодичности цепи.

2.Докажите, что сужение AX неразложимой эргодической цепи X на собственное подмножество своих состояний является обрывающейся, а ее пополнение поглощающей цепями.

3.Докажите теорему 10.9.

Указание. При необходимости можно воспользоваться рассуждениями из [11]. 4. Докажите теорему 10.10.

Указание. При необходимости можно воспользоваться рассуждениями из [11].

Задачи.

В задачах 1 – 2 заданы МВП цепи Маркова Xn.

Требуется:

(а) классифицировать состояния;

(б)найти среднее время пребывания в множестве несущественных состояний при условии, что в начальный момент цепь находится равновероятно в одном из несущественных состояний;

(в) найти вероятности lii, возвращения в каждое из состояний;

(г) найти предельные вероятности i = lim P fXn = ig ; i = 1; 4

n!1

3. По наблюдениям синоптиков в некоторой местности никогда не бывает двух дождливых дней подряд. Если сегодня дождь, то завтра с вероятностью 13 будет ясно. Если сегодня облачно, то погода не изменится с вероятностью 15 . Если же она все-таки изменится, то в половине случаев будет ясно. Если же сегодня ясно, то завтра равновероятно будет любая погода. Составить матрицу вероятностей перехода. Найти среднее число дней до ближайшего ясного дня, если сегодня облачно. Найти приближенное значение среднего числа солнечных дней в году.

Библиографические замечания.

Изложение в этом параграфе также во многом следует книге [11]. Однако, некоторые подходы являются методически новыми. Например, подход, связанный с изучением эргодических цепей путем сведения их к процессам восстановления не встречался ранее в учебной литературе.

Вероятности с запрещением и прямые и обратные уравнения, связывающие их с вероятностями переходов за n шагов подробно рассмотрены в [32]. Детальное исследование фундаментальной матрицы эргодической цепи можно найти в [11].

§ 11. Счетные марковские цепи

11.1.Вводные замечания

Исследование цепей Маркова с общим фазовым пространством интересно по многим причинам:

во-первых, действительно, многие явления естественным образом описываются наблюдениями в некотором “общем” фазовом пространстве;

во-вторых, иногда удобнее моделировать явление в более общем пространстве, так, например, благодаря аппарату дифференцирования, изучение функций непрерывного агумента значительно проще, чем дискретного;

в-третьих, любая последовательность X = fXn; n = 1; 2; : : : g может рассматриваться как марковская в достаточно широком фазовом пространстве, например, полагая Y1 = X1; Y2 = (X1; X2); : : : ; Yn = (X1; X2; : : : ; Xn); : : : , получим, что последовательность Yn - марковская.

Таким образом, при достаточно широком понимании пространства состояний любой процесс является марковским. Однако, если пространство состояний слишком широкое, то облегчения в исследовании таких процессов это не приносит. Наиболее интересные качественные свойства явлений, описываемых марковскими цепями, проявляются, по-видимому, при сравнении поведения во времени соответствующих марковских цепей с конечным, счетным, и “общим” фазовыми пространствами. При этом при переходе к общему фазовому пространству, пожалуй, наиболее существенную роль играет не столько его бесконечность, сколько компактность.

В настоящем курсе мы не будем касаться поведения марковских цепей с общим фазовым пространством и остановимся на основных особенностях поведения марковских цепей со счетным множеством состояний и прежде всего перенесем на этот случай основные понятия и определения конечных марковских цепей из § 7.

11.2.Определение

Определение и основные понятия для марковских цепей со счетным множеством состояний E = f1; 2; : : : ; n; : : : g практически не отличается от соответствующих понятий для конечных цепей. Точно также вводятся понятия независимости “будущего” от “прошлого” при известном “настоящем” и его формализация через условные (переходные) вероятности, которые образуют матрицу вероятностей переходов. Топологическая классификация состояний, опирающаяся на переходные вероятности, и вытекающее из нее приведение цепи к каноническому виду также легко переносится на случай счетного пространства состояний. Однако в этом случае приходится иметь дело с бесконечными матрицами. Формально все соответствующие матричные операции легко переносятся на случай бесконечных матриц, хотя, конечно, все трудности исследования марковских цепей со счетным фазовым пространством связаны с возможностью (скорее даже скоростью) ухода процесса на бесконечность.

Замечание 1. Также как и для конечных цепей мы не останавливаемся в данном курсе (за исключением отдельных примеров) на структурных свойствах пространства состояний марковских цепей. При этом многие интересные свойства цепей остаются за пределами курса, но они требуют специального подхода и значительного расширения курса.

Матрицы

Также как и в случае конечного множества состояний счетные марковские цепи задаются своими матрицами вероятностей перехода (МВП), которые обладают свойствами стохастических матриц. Однако в этом случае они представляют собой, вообще говоря, бесконечные вправо и вниз таблицы, а в канонической форме могут также иметь бесконечные блоки. Поэтому необходимо определить некоторые свойства и операции с такими матрицами, которые будут использоваться в дальнейшем.

Основные особенности возникают в связи с умножением бесконечных матриц.

Определение 11.1. Произведением бесконечных матриц A = [aij]i;j2E и B = [bij]i;j2E называется матрица C = [cij]i;j2E, элементы которой определяются соотношением

если соответсвующие ряды абсолютно сходятся.

Пространство мер и векторов

Поскольку нам постоянно придется иметь дело с результатами применения матриц (вероятностей переходов) к мерам и векторам в дальнейшем удобно рассматривать их как точки в соответствующих пространствах и вообще использовать операторную терминологию, которая вводится в

настоящем подразделе. Напомним, что в счетных пространствах мера любого множества опреде-

P

ляется мерами одноточечных множеств (атомов) его составляющих, так что (A) = i2A ai; где ai = (fig) мера соответствующего одноточечного множества.

Итак, если f = ff(i); i 2 Eg функция на E, = fai; i 2 Eg мера на E, и P МВП счетной марковской цепи (которую можно рассматривать как оператор, применяемый к функциям и мерам), то через P f обозначается функция P f : E ! E со значениями

При этом, конечно, необходимо требовать абсолютную сходимость соответствующих рядов. Поскольку мы имеем дело здесь со стохастическими матрицами, то для соответствующей сходимости достаточно, например, для функций их ограниченности, а для мер их конечности, т.е. сходи-

P

мости ряда ai. Поэтому соответствующие операторы будем рассматривать на множествах B

i2E

ограниченных функций и @ конечных мер.

11.3.Классификация состояний

Топологическая классификация, основанная непосредственно на свойствах переходной матрицы или графа переходов полностью совпадает с соответствующей классификацией для конечных цепей, поэтому она без изменений переносится на случай цепей со счетным фазовым пространством. Сохраняются понятия существенных, несущественных, сообщающихся, периодических состояний, а также свойства разбиения их на классы и каноническая форма МВП.

Однако, бесконечность фазового пространства приводит к ряду особенностей в поведении цепей с таким фазовым пространством.

Чтобы легче проследить причины и специфику поведения цепей со счетным фазовым пространством, рассмотрим особенности их поведения на отдельных примерах.

Особенности поведения марковских цепей со счетным фазовым пространством

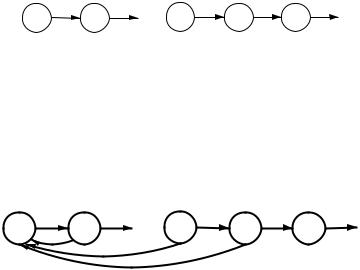
Пример 1. Для конечных марковских цепей множество несущественных состояний всегда конечно, так что такая цепь в конце концов всегда оказывается в некотором замкнутом множестве состояний (классе), в котором остается неограниченно долго, что обеспечивает возвратность состояний замкнутого класса. Рассмотрим марковскую цепь с пространством состояний E = f0; 1; 2; : : : g; граф переходов которой изображен на рис.11.1.

Очевидно, что все состояния такой цепи несущественны, так что она неограниченно долго остается в множестве несущественных состояний, посетив каждое из них всего 1 раз. Естественно

Рис. 11.1. Граф переходов марковской цепи из несущественных состояний

ни о какой возвратности здесь не может быть и речи, хотя, с другой стороны, время достижения каждого состояния или любого множества в этом примере достаточно легко вычисляется.

Пример 2. Изменим пример 1 следующим образом (см. рис.11.2).

1 - p n

Рис. 11.2. Граф переходов марковской цепи из существенных невозвратных состояний

Очевидно, что если в этом примере все 0 < pi < 1, то все состояния сообщающиеся, так что цепь неразложима и образует один замкнутый класс сообщающихся состояний. Вычислим вероятность возвращения цепи в состояние “0” впервые за время n. Так как возвращение в 0 за n шагов возможно лишь вдоль единственной траектории (0; 1; : : : ; n 1; 0), то имеем

l00(n) = p0p1 : : : pn 1(1 pn):

Таким образом, вероятность возвращения в состояние 0 когда-нибудь равна

l00 = X l00(n) = 1 lim p0p1 : : : pn 1pn;

n!1

n 1

так что выбирая числа pi так, чтобы произведение имело конечное значение, получим, что вероятность возвращения в состояние 0 меньше 1, что в силу следствия 10.1 к теореме 10.1 невозможно для конечных цепей.

Пример 3. Вычислим применительно к предыдущему примеру среднее время возвращения

m00 = X nl00(n) = 1l00(1) + 2l00(2) + : : : nl00(n) + = n 1

=1p0(1 p1) + + np0p1 : : : pn 1(1 pn) + =

=p0 p0p1 + : : : np0p1 : : : pn 1 np0p1 : : : pn 1pn + =

XY

=pk:

n 0 0 k n

Поэтому выбирая в предыдущем примере числа pi так, чтобы

получим марковскую цепь, для которой состояние 0 возвратно, но среднее время возвращения бесконечно, что в силу следствия 10.2 к теореме 10.1 невозможно для конечных цепей.

Эти принципиальные особенности поведения марковских цепей с бесконечным фазовым пространством определяют также и сложности их исследования.