
Курс_лекций_по_теории_случайных_процессов
.pdf
§ 14. Классификация состояний. Устойчивость |
101 |
14.2.Устойчивость
Из определения интенсивностей переходов соотношением (13.1) и их свойств в теореме 13.1 следует
0 i 1.
Определение 14.4. Cостояние i называется мгновенным (или неустойчивым), если i = 1.
Такое состояние не наблюдаемо, т.к. процесс мгновенно покидает его. В дальнейшем будет рассматриваться случай, когда все i < 1, т.е. только процессы с устойчивыми состояниями. Заметим, что в случае бесконечного пространства состояний, E = f0; 1; : : : g, возможен случай, когдаi < 1, но i ! 1 при i ! 1. Это приводит к тому, что процесс “уходит на бесконечность” за конечное время (см. далее пример 1 и рисунок к нему.
Определение 14.5. Процесс называется устойчивым, если на любом конечном интервале он совершает лишь конечное число скачков (переходов).
Теорема 14.2 (Критерий устойчивости). Пусть X(t) стандартный марковский процесс, Snмоменты его скачков, тогда для устойчивости процесса необходимо и достаточно, чтобы
()
|
X |
1 |
= 1 = 1: |
(14.5) |
по |
XSn |
|||
P |
всем n |
|||
|
|
|
|
Доказательство этой теоремы выходит за рамки настоящего курса. Мы ограничимся тем, что прокомментируем это условие устойчивости на примере процесса чистого размножения.
Определение 14.6. Процессом чистого размножения называется дискретный стандартный марковский процесс с вполне упорядоченным множеством состояний, переходы (скачки) в котором возможны только в последующие состояния, т.е. переход из состояния i возможен только в состояние i + 1 с интенсивностью i. Для такого процесса интенсивности переходов определяются соотношением
(
ij =
i; j = i + 1;
0; j 6= i + 1:
Пример 1. Рассмотрим процесс чистого размножения. Пусть X(0) = 0. Тогда X(Sn) = n и, следовательно, X(Sn) = n. Таким образом, согласно критерию устойчивости процесс устойчив тогда и только тогда, когда
X 1 = 1: (14.6)
n
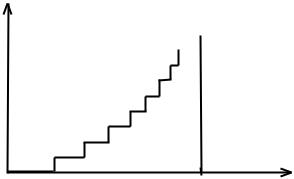
Заметим, что члены этого ряда представляют собой средние длительности пребывания процесса в соответствующих состояниях. Поэтому расходимость этого ряда означает, что процесс развивается в среднем “бесконечно долго”. В противном случае, т.е. при сходимости ряда (14.6) последовательность n достаточно быстро расходится, например, при n n1+ скачки очень быстро накапли-
ваются, так что процесс “уходит в бесконечность” за конечное время T , такое, что MT = Pn 1
n
(см. рис.14.1). При этом поведение процесса за пределами времени T становится неопределенным, а уравнения Колмогорова утрачивают единственность.
Недостатком приведенного выше критерия устойчивости является трудность проверки его условий. Существуют сравнительно просто проверяемые достаточные условия устойчивости (или регулярности) процесса.
Теорема 14.3 (Достаточное условие устойчивости). Для устойчивости процесса достаточно либо
(1)равномерной ограниченности интенсивностей i : i C < 1, либо
(2)возвратности всех состояний вложенной цепи.
102 |
Глава 4. Скачкообразные марк. и полумарк. процессы |
X (t)
...
t
T
Рис. 14.1. Процесс чистого размножения XSn
Для устойчивых процессов справедлива
Теорема 14.4. Если X(t) устойчивый процесс со счетным множеством состояний, то любая из систем (14.3, 14.4) имеет единственное решение.
Доказательства этих теорем не приводятся ввиду их сложности; их можно найти в специальной литературе, см., например, [10].
Приведенные теоремы показывают, что устойчивый стандартный марковский процесс полностью определяется своей матрицей интенсивностей переходов. Это позволяет предложить другой способ задания таких процессов, основанный на его представлении в виде размеченного графа. За вершины графа примем состояния процесса, направленные дуги соединяют такие состояния i и j, для которых ij > 0, при этом соответствующая дуга помечается этим значением. Такой граф называется размеченным графом переходов марковского процесса. Пример размеченного графа переходов марковского процесса чистого размножения из примера 1 приведен на рисунке 14.2.
0 1 n
: : : : : :
0 - 1 - 2 n - n + 1
Рис.14.2. Размеченный граф переходов процесса чистого размножения.
14.3.Связь марковских процессов с цепями
Естественно, марковские процессы имеют самую тесную и глубокую связь с цепями. В разделе 13.3. уже была введена вложенная марковская цепь Yn = X(Sn) дл процесса X(t). В настоящем разделе рассмотрим еще целое семейство марковских цепей, связанных с исходным марковским процессом.
Пусть X = fX(t); t 2 R+g марковский процесс cо счетным фазовым пространством E. Выбирая различные положительные числа h, рассмотрим семейство последовательностей Xbn(h) =
Xnh; n = 0; 1; 2:::.
Лемма 14.5. Для марковского процесса X = fX(t); t 2 R+g последовательность Xbn(h) = Xnh; n = 0; 1; 2::: образует марковскую цепь для любого положительные числа h.

§ 14. Классификация состояний. Устойчивость |
103 |
Доказательство выполнить самостоятельно в качестве упражнения 3. |
|
Определение 14.7. Последовательность Xn(h) = Xnh называется остовом марковского процесса с шагом h.
Опираясь на связь между марковским процессом и его остовом на марковские процессы можно перенести многие свойства цепей и, прежде всего, классификацию его состояний. Приведем здесь эти вопросы конспективно, так как в предыдущем разделе была предложена независимая классификация состояний марковских процессов.
Очевидно, что для каждой из марковских цепей Xn(h) при различных h можно провести классификацию ее состояний в соответствии с определениями предыдущих глав. Чтобы эту классификацию можно было перенести на соответствующий процесс, необходимо убедиться, что любой из остовов марковского процесса имеет одинаковую классификацию.
Лемма 14.6. Все остовы некоторого марковского процесса имеют одну и ту же классификацию.
Доказательство провести самостоятельно в виде упражнения 4. |
|
Остовы марковских процессов удобно использовать при их имитационном моделировании. Наряду с остовом и вложенной марковской цепью часто удобно пользоваться другими модификациями марковских процессов.
Замечание 1. В разделе 13.3. было предложено конструктивное описание марковского процесса, при котором процесс совершает скачки через случайные показательно распределенные с различными средними значениями i 1 интервалы времени. Наряду с этой конструкцией в приложениях часто бывает полезно рассматривать другую эквивалентную конструкцию марковского процесса, при которой исходный процесс совершает скачки через случайные одинаково распределенные интервалы времени. Для описания этой конструкции обозначим через c максимальное из значенийi; c = maxi2E i, и рассмотрим скачкообразный процесс, который проводит в каждом из своих состояний показательно распределенное с параметром c время, а затем из состояния i с вероятностью cij переходит в состояние j, а с вероятностью 1 ci остается в состоянии i. Можно показать, что построенный таким образом процесс является марковским, а его КМР совпадают с КМР исходного процесса, т.е. процессы и эквивалентны, а следовательно стохастически неразличимы.
14.4.Дополнения
Вопросы для контроля.
1.Дайте определение несущественного состояния марковского процесса.
2.Дайте определение сообщающихся состояний марковского процесса.
3.Что называется остовом марковского процесса?
4.Дайте определение неразложимого марковского процесса.
5.Сформулируйте теорему солидарности для марковских процессов.
6.Дайте определение мгновенного, устойчивого и поглощающего состояний марковского про-
цесса.
7.Дайте определение устойчивого марковского процесса.
8.Поясните поведение не устойчивого марковского процесса.
9.Приведите критерий устойчивости марковского процесса.
10.Сформулируйте теорему о существовании и единственности решений дифференциальных уравнений Колмогорова для переходных вероятностей устойчивых марковских процессов.
11.Что такое граф переходов стандартного марковского процесса?
Упражнения.
1. Докажите лемму 1.
^
2 . Выпишите функционал для определения с.в. Ti.
104 |
Глава 4. Скачкообразные марк. и полумарк. процессы |
3. Докажите лемму 14.2.
Указание: используйте формулу полной вероятности и марковское свойство процесса.
4.Докажите лемму 14.5.
5.Докажите лемму 14.6.
Библиографические замечания.
Классификация состояний марковских процессов практически совпадает с классификацией состояний цепей и следует классификации, предложенной Колмогоровым [19] и Феллером [29]. Доказательство критерия устойчивости (теорема 14.2) можно найти у Феллера [29]. Связь марковских процессов с цепями подробно исследовал Чжун Кай-Лай [32]. Конструкцию, изложенную в замечании 1 предложил Серфозо.

§ 15. Свойства марковских процессов |
105 |
§ 15. Свойства марковских процессов
В этом параграфе будут изложены основные свойства марковских скачкообразных процессов. Приведем сначала уравнения для вероятностей состояний, которые лежат в основе анализа марковских процессов, затем на их основе получим методы анализа распределения времени достижения отдельного состояния или множества состояний и связанного с ним распределения времени пребывания в множестве состояний. Затем рассмотрим поведение процесса в замкнутом множестве состояний.
15.1.Уравнения для вероятностей состояний
Решение уравнений для переходных вероятностей (13.2) (13.4) редко удается получить в явном виде, да они и не представляют особого практического интереса. Однако используя уравнение (13.2), легко получить уравнение для вектора вероятностей состояний процесса p~(t) = fpk(t); k 2 Eg, где
pk(t) = P fX(t) = kg |
(15.1) |
с любым начальным распределением = fak; k 2 Eg, где |
|
ak = pk(0) = PfX(0) = kg; k 2 E: |
(15.2) |
Действительно, умножая уравнение (13.2) на вектор начального распределения слева, получим
|
|
d~pT (t) |
= p~T (t) |
|
(15.3) |
|
|
|
dt |
|
|
||
|
|
|
|
|
||
или в координатной форме |
X |
|
2X6 |
|
||
pk(t) = |
|
(15.4) |
||||
pi(t) ik = pk(t) k + |
pi(t) ik; |
|||||
|
i2E |
|
i E; i=k |
|
||
которое необходимо решать с начальным условием (15.2).
В случае конечного пространства состояний E система уравнений (15.4) с начальным условием (15.2) представляет собой задачу Коши, и, следовательно, имеет единственное решение. В случае счетного пространства состояний E для существования и единственности достаточно потребовать выполнения условия устойчивости процесса (теорема 14.3)
При составлении уравнений (15.2, 15.3) непосредственно с помощью графа переходов марковского процесса удобно пользоваться следующим правилом.
Правило составления дифференциальных уравнений для вероятностей состояний марковского процесса. Производная вероятности некоторого состояния k равна алгебраической сумме произведений вероятностей состояний на интенсивности переходов, взятых со знаком “плюc” для входящих в k стрелок и “минус” для выходящих.
15.2.Время достижения
Используем дифференциальные уравнения для вероятностей состояний для изучения времени достижения некоторого состояния (или подмножества состояний) и времени пребывания процесса в некотором подмножестве состояний. Ясно, что время пребывания процесса в некотором подмножестве состояний совпадает с временем достижения его дополнения, поэтому достаточно изучить какую-либо одну из этих характеристик. Рассмотрим, например, время достижения. Ясно, что время достижения некоторого подмножества совпадает с моментом попадания процесса в это подмножество, если запретить выход из него. Поэтому методика вычисления распределения времени достижения сводится к решению дифференциальных уравнений Колмогорова для вероятностей состояний для модифицированного процесса, в котором выход из рассматриваемого подмножества состояний запрещен. Для модификации достаточно удалить в размеченном графе переходов
106 |
Глава 4. Скачкообразные марк. и полумарк. процессы |
все дуги, выходящие из поглощающего подмножества, т.е. рассмотреть сужение процесса на рассматриваемое подмножество. Вместо того, чтобы приводить общую методику вычисления времени достижения, рассмотрим ее на конкретном прикладном примере.
Пример 1. Дублированная система. Рассмотрим систему облегченного дублирования с восстановлением из примера 12.1 с тремя состояниями E = f0; 1; 2g, где состояние i означает число элементов, находящихся в состоянии отказа, и исследуем распределение времени до первого отказа. Длительности исправной работы в основном и резервном состояниях и время ремонта имеют показательные распределения с параметрами ; ; соответственно. Для вычисления распреде-
^
ления времени до первого отказа рассмотрим поведение марковского процесса X(t), означающего число неисправных элементов, до момента его первого попадания в состояние 2, для чего поместим в это состояние поглощающий экран, запретив выход из него. Тогда распределение F (t) времени
^
T до первого отказа исходной системы совпадает с вероятностью того, что процесс X(t) находится в состоянии 2,
f g f ^ g
F (t) = P T t = P X(t) = 2 :
Граф переходов такого процесса для системы облегченного дублирования (когда дублирующий элемент находится в облегченном режиме работы) с одной ремонтной бригадой представлен на рис. 15.1.
+ hch 

























 hch
hch
|
||
1 |
2 |
3 |
hh |
|
|
c |
|
|
|
|
|
Рис.15.1. Размеченный граф переходов для модифицированного
^
процесса X(t).
Поэтому, согласно правилу составления дифференциальных уравнений для вероятностей состояний марковских процессов (см. раздел. 15.1.), система дифференциальных уравнений для вероятностей его состояний имеет вид
p0(t) = ( + ) p0(t) + p1(t);
p1(t) |
= |
( + ) p0(t) ( + ) p1(t); |
p2(t) |
= |
p1(t); |
9
=
(15.5)
;
которую следует решать с начальным условием |
|
|
p0(0) = 1; p1(0) = p2(0) = 0: |
(15.6) |
|
Для решения этой системы воспользуемся методом преобразований Лапласа |
|
|
1 |
|
|
p~k(s) = Z0 |
e st pk(t) dt: |
|
Так как последнее из уравнений (15.6) решается простым интегрированием, то, переходя в первых двух уравнениях системы (15.6) к преобразованиям Лапласа и замечая, что
1 |
|
|
1 |
|
Z |
e st pk(t) dt = e st pk(t) |
|
01 + Z |
e st pk(t) dt = sp~k(s) pk(0); |
0 |
|
0 |
|
|
|
|
|
|
|

§ 15. Свойства марковских процессов |
107 |
для функций p~k(s) получим с учетом начальных условий (15.6) систему алгебраических уравнений
s p~1(s) = ( + ) p~0 |
(s) ( + ) p~1(s) |
|
|||||||||||
s p~0(s) 1 = |
( + ) p~0(s) + p~1(s) |
: |
|||||||||||
Записывая последнюю систему в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
( + ) p~0(s) + ( + + s) p~1 |
(s) = 0; |
||||||||||||
( + + s) p~0 |
(s) |
|
p~1 |
(s) = 1; |
|
||||||||
легко найти ее решение, например, по правилу Крамера, |
|
|
|
|
|||||||||
p~0(s) = |
|
|
|
|
+ +s |
|
|
|
|
||||
( + +s)( + +s) ( + ) : |
|
||||||||||||
p~1(s) = |
|
|
|
|
|
+ |
|
|
|
|
|||
( + +s)( + +s) ( + ) |
|
||||||||||||
Для вычисления обратного преобразования разложим функцию p~1(s) на простые дроби |
|||||||||||||
p~1(s) = |
A1 |
|
+ |
|
A2 |
|
(15.7) |
||||||
s + s1 |
s + s2 |
||||||||||||
|
|
|
|
|
|||||||||
и вычислим коэффициенты этого разложения из системы уравнений |
|
||||||||||||
A1s2 |
+ A2s1 |
= + ; |
|
||||||||||
A1 + A2 |
= |
0 |
|
|
|
|
|||||||
где s1; s2 корни знаменателя выражения для p~1(s) (характеристического уравнения системы
(15.6)),
( + + s) ( + + s) ( + ) = s2 + (2 + + ) s + ( + ) = 0;
взятые, для наглядности, со знаком “минус”, равные в данном случае в терминах безразмерных коэффициентов = и =
s1;2 = |
|
(2 + + p( + )2 + 4 ): |
2 |
Переходя теперь в (15.7) к обратному преобразованию, найдем
p1(t) = A1e s1 t + A2e s2 t;
откуда простым интегрированием получим ф.р. длительности до первого отказа системы, которая после подстановки значений коэффициентов A1 и A2 примет вид
|
|
|
|
|
F (t) = p2(t) = Z |
t |
2 |
|
|
s1 |
|
|
|||||||
|
|
|
|
|
p1(u) du = 1 |
1 |
|
|
|||||||||||
|
|
|
|
|
|
e s1t |
|
e rt |
; |
(15.8) |
|||||||||
|
|
|
|
s1r |
s2 |
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ние |
2 |
s |
1 |
p |
|
|
|
2 |
|
|
s1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||||
где r = s |
|
|
= ( + )2 + 4 . Наконец, для функции надежности системы получим выраже- |
||||||||||||||||
|
|
|
|
|
R(t) = 1 p2(t) = |
|
e s1t 1 |
|
e rt : |
|
(15.9) |
||||||||
|
|
|
|
|
s1r |
s2 |
|
||||||||||||
Заметим, что выражения (15.8) и (15.9) для ф.р. длительности до первого отказа и функции надежности сохраняется также для систем нагруженного (при = ) и не нагруженного (при= 0) дублирования. Изменяются лишь характеристическое уравнение и соответственно значения s1; s2 его корней.
Вычисления показывают, что средняя длительность безотказной работы mс восст. системы облегченного дублирования с восстановлением равна
mс восст. = 2 + + 1:
1 +

108 |
Глава 4. Скачкообразные марк. и полумарк. процессы |
Откуда для систем нагруженного (при = 1) и не нагруженного (при = 0) дублирования средняя длительность работы системы равна соответственно
mс восст. |
= |
3 + |
для системы нагруженного дублирования; |
|
2 |
||||
mс восст. |
= |
2 + |
для системы не нагруженного дублирования: |
|
|
||||
|
|
|
Как будет показано в дальнейшем (см. пример 17.1) средняя длительность безотказной работы системы нагруженного дублирования без восстановления, например, равна mбез восст. = 32 1, так что коэффициент
= = среднее время работы элемента ;
среднее время ремонта элемента
определяет эффективность восстанавливаемых систем по отношению к невосстанавливаемым.
Рассмотрим теперь основные свойства неразложимых процессов.
15.3.Предельная теорема для марковских процессов
Основные свойства неразложимых марковских цепей сохраняются также и для неразложимых процессов. Прежде чем переходить к доказательству соответствующей предельной теоремы напомним формулы (14.1, 14.2) разложения по моментам первого и последнего достижения из раздела 14.1.
|
|
ije it + Z0 |
t |
|
pij(t) |
= |
dFij(u)pjj(t u); |
(15.10) |
|
|
|
ije it + Z0 |
t |
|
pij(t) |
= |
pij(t u)dFjj(u): |
(15.11) |
Теорема 15.1. Для переходных вероятностей стандартного марковского процесса существуют пределы
|
lim pij(t) = ij; |
(15.12) |
||||
|
t!1 |
|
||||
причем |
|
|||||
(1) |
если состояния i; j положительно возвратны и принадлежат одному классу сообщающихся |
|||||
|
состояний, то |
|
||||
|
1 |
|
|
|
|
|
|
ij = |
|
|
= j > 0; |
(15.13) |
|
|
jfjj |
|||||
(2) |
если состояние j возвратно и нулевое или невозвратно, а i любое, то |
|
||||
|
|
ij = 0; |
(15.14) |
|||
(3) |
если i несущественное, а j положительно возвратное, то |
|
||||
|
ij = |
Fij(1) |
; |
(15.15) |
||
|
|
|
jfjj |
|
||
|
1 |
|
|
|||
R
где Fij(t) ф.р. времени первого достижения, fjj = tdFjj(t) среднее время первого возвра-
0
щения, Fij(1) = lim Fij(t) вероятность достижения состояния j из состояния i.
t!1

§ 15. Свойства марковских процессов |
|
|
|
|
|
|
|
|
|
|
109 |
|||||
Доказательство. Переходя к преобразованиям Лапласа и Лапласа-Стилтьеса: |
||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
p~ij(s) = Z0 |
e stpij(t)dt; |
|
f~jj(s) = Z0 |
e stdFjj(t); |
|
|
||||||||||
в соотношении (15.10) найдем |
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
p~ij(s) = |
|
|
|
|
+ f~ij(s)~pjj(s) |
|
|
|
|||||||
|
s + i |
|
|
|
|
|||||||||||
При i = j из этого соотношения следует |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p~jj(s) = |
|
|
|
1 |
|
|
|
: |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
(s + j)(1 f~jj(s)) |
|
|
|
||||||||
Для j 6= i имеем |
p~ij(s) = |
|
|
|
|
|
f~ij(s) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
: |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
(s + j)(1 f~jj(s)) |
|
|
|
|||||||||
Пользуясь тауберовой теоремой [9] из анализа вычислим предел |
|
|
|
|||||||||||||
lim pij(t) = |
lim sp~ij(s) = lim |
|
|
|
f~ij(s) |
|
= |
|||||||||
|
|
|
|
1 f~jj(s) |
|
|||||||||||
t!1 |
s!+0 |
|
|
|
s!+0 (s + j) |
s |
|
|
||||||||
= |
|
f~ij(0) |
|
= |
|
Fij(1) |
: |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
jfjj0 (0) |
|
jfjj |
|
|
|
|
|
|
|||||||
Если состояния i; j принадлежат одному и тому же классу сообщающихся состояний i 2 Ej, то Fij(1) = 1 и полученное соотношение приводит к (15.13); если они принадлежат различным классам i 62Ej, то Fij(1) = 0 и ij = 0. Если состояние j невозвратно или возвратное нулевое, то fjj = 1, так что предел равен нулю (случай (2)). Наконец, если i несущественно, а j положительно возвратно, то Fij(1) представляет собой вероятность поглощения траектории процесса, выходящего из состояния i, классом состояний, содержащим состояние j, что представляет случай (3). Таким образом, все утверждения теоремы доказаны.
Замечание 1. Как следует из приведенной теоремы предельные вероятности имеют ясный “физический” смысл и играют важную роль при анализе марковских процессов. Поэтому важно иметь доступные способы их вычисления. Прямые вычисления с помощью предельных соотношений обычно затруднительны. Однако, как не трудно видеть предельные вероятности ~ = f i; i 2 Eg удовлетворяют системе алгебраических уравнений
0 = ~ ;
или в координатной форме
X
i ij = 0; |
(15.16) |
i2E
которая называется системой уравнений равновесия (СУР). Эта система, как однородная система с вырожденным определителем, имеет бесконечно много решений. Однако единственное (для неразложимой цепи) вероятностное решение определяется из нее дополнительным условием нормировки
X
i = 1: |
(15.17) |
i2E
Интересно отметить связь этого инвариантного (стационарного) распределения с соответствую-
^
щим распределением ~ для вложенной по моментам скачков марковской цепи. Для этого заметим,

110 |
Глава 4. Скачкообразные марк. и полумарк. процессы |
что в силу определения переходных вероятностей pij вложенной цепи формулой (13.8) pij = ij
i
последние удовлетворяют системе уравнений
|
|
^j = |
^i |
ij |
: |
|
|
|
|
|
|
|
|||||
|
|
|
i6=j |
i |
|
|
|
|
|
|
|
X |
|
|
|
|
|
Замечая, что ii = i из этого соотношения найдем |
|
|
|
|||||
X |
|
|
|
|
^i |
|
||
|
^i |
ij = 0 и следовательно |
i = |
; |
||||
|
i |
|
|
|
|
i |
||
i2E |
|
|
|
|
|
|
||
или
1
^i = i i = fii :
Заметим, что так как ^i = mii1, то mii = fii, т.е. среднее время возвращения процесса в некоторое состояние совпадает со средним числом переходов его вложенной цепи до возвращения в это состояние.
15.4. Эргодическая теорема
Рассмотрим функционал
Gt(X( )) = Z |
t |
|
g(X(u))du; |
(15.18) |
0
где g( ) функция, заданная на множестве состояний марковского процесса. Интегрирование ведется вдоль траектории процесса. Для индикаторной функции, например,
(
g(x) = 1j(x) =
1; x = j;
0; x 6= j
значением функционала Gt(X( )) является время, проведенное в состоянии j за время t. В частности, например, для процесса, описывающего поведение технического устройства с двумя состояниями исправным и неисправным значения такого функционала показывают время исправной и неисправной работы.
Теорема 15.2 (Эргодическая теорема). Если X(t) неразложимый положительно возвратный стандартный марковский процесс, а функция g(x) ограничена, то среднее по времени от функционала (15.18) сходится по вероятности и с вероятностью 1 к его математическому ожиданию относительно инвариантного распределения = f k; k 2 Eg,
lim Gt = |
S1(i) |
= M g(X( )) = kg(k): |
(15.19) |
|||||
R |
||||||||
|
|
M |
g(X(u))du |
|
X |
|
||
1 |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
t!1 t |
M S1(i) |
|
k2E |
|
||||
|
|
|
|
|
|
|
|
|
Доказательство аналогично доказательству эргодической теоремы для марковских цепей. Пусть t фиксированное время, Sn(e) = Sn моменты возвращения в фиксированное состояние, скажем e, Ne(t) = N(t) число возвращений в это состояние за время t. Тогда справедливо представление
t |
Z |
t |
N(t) |
Sn |
g(X(u))du + t |
t |
g(X(u))du: |
||
g(X(u))du = t |
n=1 |
Z |
Z |
||||||
1 |
1 |
XSn 1 |
1 |
|
|
||||
|
0 |
|
|
|
|
SN(t) |
|
||
При t ! 1 второе слагаемое справа сходится к нулю в силу ограниченности подынтегральной функции и конечности в среднем (в силу положительной возвратности процесса) интервала
