
Курс_лекций_по_теории_случайных_процессов
.pdf
§ 7. Определение. Основные свойства |
41 |
|
|
|
|
|
pM |
|
|
|
|
|
|
|
p2 |
pM-1 |
|
|
|
|
|
p |
p1 |
|
|
p1 |
||
p |
0 |
1 |
2 |
... |
M-1 |
M |
||
1 |
||||||||
0 |
|
|
p |
|
p |
|
p |
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|||
|
|
|
|
|
0 |
|
0 |
1
Рис. 7.3. Граф переходов для МЦ из примера 3.
времени. Аналогично этому предположим, что с вероятностями q и 1 q за единицу времени происходит восстановление неисправного устройства или продолжается его ремонт также независимо от его предыдущей истории.
Тогда процесс функционирования устройства описывается марковской цепью с переходной матрицей
P = |
1 p |
p |
: |
|
q |
1 q |
|
Соответствующий граф переходов показан на рис. 7.4
p
1 - p |
1 |
2 |
1- q |
q
Рис. 7.4. Граф переходов МЦ из примера 4.
Пример 5. Обобщим предыдущий пример, рассматривая отказы различных агрегатов. Тогда можно расширить пространство состояний, допуская несколько типов неисправностей системы (например для автомобиля это могут быть неисправности двигателя, системы питания, электрооборудования, тормозов и т.д.). Заметим, что исправное состояние тоже можно расширить, вводя различного вида предотказовые состояния, позволяющие контролировать систему и управлять ее работой. Впрочем, конкретное описание системы относится скорее к области искусства моделирования, чем к изучению марковских цепей.
Пусть имеется, например, всего три типа отказов. Обозначим через pi; i = 1; 2; 3, вероятность возникновения отказа i-го типа и через qi вероятность восстановления такого отказа за единицу времени. Предположим дополнительно, что два отказа не могут возникнуть одновременно, и во время ремонта не может возникнуть отказ другого типа (хотя в жизни такое, конечно, бывает). В качестве упражнения 3 предлагается составить соответствующую МВП и построить граф переходов для этого примера.
Пример 6. В геологии при стратиграфических исследованиях пород наблюдения проводятся через определенные фиксированные интервалы, например, через 0,5 м. вдоль стратиграфического разреза. При этом состояниями являются типы наблюдаемых пород. Если A означает песчаник, B известняк и C сланец, то последовательность наблюдений вдоль разреза может иметь вид: AAABBCBCACCCBA, который говорит о том, что верхний слой рассматриваемого разреза составляет песчаник толщиной 1,5 м., следующий слой толщиной 1 м. состоит из известняка и т.д. В этой модели аргументом является расстояние, а “время пребывания” в состоянии определяет толщину пласта, измеренную в дискретных единицах.
42 Глава 3. Цепи Маркова
Предположим, что при исследовании стратиграфического разреза статистика позволяет прийти к выводу о независимости следования пород в разрезе от предыдущих наблюдений при фиксированном типе неблюдаемой породы. Тогда изучаемое явление может быть описано марковской цепью с числом состояний, равным числу типов пород. Обозначая состояния разреза теми же буквами, что и породы: E = fA; B; C; : : : g в качестве упражнения 4 предлагается выписать МВП и нарисовать граф переходов марковской цепи для приведенного примера.
Пример 7. (Модель Эренфеста для диффузии [11]). Рассмотрим газ, заключенный в сосуде, разделенном на две части A и B проницаемой мембраной. В каждый из дискретных моментов времени выбирается одна из молекул и перемещается из той части, где она находилась в другую. Рассмотрим для простоты случай трех молекул (в общем случае произвольного числа молекул ситуация аналогична). В качестве состояний рассмотрим векторы x = fx1x2x3g, где xi = 1, если i- я молекула находится в области A, и xi = 0 в противоположном случае. Заметим, что возвращение из состояния x в x возможно только за четное число шагов. МВП имеет вид
001 |
0 |
000 |
001 |
010 |
100 |
011 |
101 |
110 |
111 |
1 |
1=3 |
0 |
0 |
0 |
1=3 |
1=3 |
0 |
0 |
|||
000 |
|
0 |
1=3 |
1=3 |
1=3 |
0 |
0 |
0 |
0 |
C |
100 B |
1=3 |
0 |
0 |
0 |
0 |
1=3 |
1=3 |
0 |
||
010 |
B |
1=3 |
0 |
0 |
0 |
1=3 |
0 |
1=3 |
0 |
C |
011 B |
0 |
1=3 |
1=3 |
0 |
0 |
0 |
0 |
1=3 C |
||
|
B |
|
|
|
|
|
|
|
|
C |
101 B |
0 |
1=3 |
0 |
1=3 |
0 |
0 |
0 |
1=3 C |
||
|
B |
|
|
|
|
|
|
|
|
C |
110 B |
0 |
0 |
1=3 |
1=3 |
0 |
0 |
0 |
1=3 C |
||
|
B |
|
|
|
|
|
|
|
|
C |
111 B |
0 |
0 |
0 |
0 |
1=3 |
1=3 |
1=3 |
0 |
C |
|
|
B |
|
|
|
|
|
|
|
|
C |
|
@ |
|
|
|
|
|
|
|
|
A |
Рекомендуем читателю в качестве упражнения 5 закончить составление матрицы и нарисовать граф переходов марковской цепи модели Эренфеста для диффузии.
Пример 8. (Распределение населения по группам профессий [11]). Пусть fA1; A2; A3g
множество типов профессий, или видов занятости. Сын может избрать любой тип профессии, однако этот выбор зависит от профессии отца. Следующая таблица составлена по данным одного из социологических исследований, проведенных в Англии и Уэльсе (цитируем по книге [11]). В ней показана доля детей, выбравших тот или иной вид занятости в зависимости от типа профессии отца.
ОтецnСын |
0 |
A1 |
A2 |
A3 |
|
0; 448 |
0; 484 |
1 |
|
A1 |
|
0; 068 |
||
A2 |
@ |
0; 054 |
0; 699 |
0; 247 |
A3 |
0; 011 |
0; 503 |
0; 486 A |
Пусть Xn вид занятости, избранный представителем n-го поколения семьи. Тогда МВП совпадает с таблицей, приведенной ранее. В качестве упражнения 6 предлагается нарисовать соответствующий граф переходов.
В дальнейшем будет показано, как по этим данным сделать прогноз распределения населения по группам профессий.
Во всех приведенных примерах мы предполагали независимость будущего от прошлого при известном настоящем, а соответствующие переходные вероятности считали заданными. При реальном моделировании случайных явлений и процессов это предположение требует серьезного теоретического обоснования или статистической проверки. Значения переходных вероятностей также получаются либо путем теоретических выводов, либо должны быть оценены методами математической статистики.
Замечание 1. Как видно из приведенных примеров, марковские цепи моделируют поведение физических, технических, экономических, социальных и других систем, которые могут находиться в каком-либо из состояний своего фазового пространства. С другой стороны, мы рассматриваем цепь Маркова как математический объект случайный процесс, принимающий значения из некоторого множества допустимых значений, называемого пространством состояний или
§ 7. Определение. Основные свойства |
43 |
множеством значений. Поэтому в терминологии марковских цепей сохраняется некоторая двойственность, отражающая двойственность их происхождения: состояния значения, фазовое пространство множество значений. Подчеркнув эту двойственность терминологии, мы не будем стремиться уходить от нее, напротив, будем использовать в зависимости от удобства те или иные термины.
7.3.Основные задачи теории цепей Маркова
В этом разделе рассматриваются основные задачи теории марковских цепей, некоторые простые простые из которых мы в состоянии решить уже теперь.
Время пребывания в состоянии.
Найдем распределение времени непрерывного пребывания марковской цепи в отдельном состоянии. В примере 4 эта характеристика означает время непрерывной исправной работы устройства (или длительность периода неисправности), в примере 6 эта величина характеризует толщину соответствующего пласта, в примере 8 это будет количество поколений одной семьи, избравших один и тот же тип профессии.
Пусть Ti число возвращений (время непрерывного пребывания) марковской цепи в состоянии i, так что Ti + 1 представляет собой время первого выхода из этого состояния. Нетрудно понять, что событие fTi = kg происходит тогда и только тогда, когда цепь k 1 раз возвращается в состояние i, а затем покидает его. Так как при фиксированном i эти события независимы, то ясно, что с.в. Ti имеет геометрическое распределение:
PifTi = kg = (1 pii)piik 1; k = 1; 2; : : : |
(7.4) |
Заметим, что в модели Эренфеста для диффузии px;x = 0, поэтому PfTx = 1g = 1.
Вероятности перехода за n шагов.
Обозначим через
p(ijn) = PfXn = j=X0 = ig
вероятность перехода марковской цепи из состояния i в состояние j за n шагов, а через P (n) = [p(ijn)]
соответствующую матрицу вероятностей переходов и найдем эти вероятности. Ясно, что p(0)ij = ij,
где ij - символ Кронекера: ij = 1, если j = i и ij = 0, если j 6= i, и p(1)ij = pij , т.е. P (0) = I и
P (1) = P .
Теорема 7.3. Для всех n 0 справедливо равенство
P (n) = P n |
(7.5) |
Доказательство проводится по индукции. Используя формулу полной вероятности и свойство марковости, получаем:
pij(2) = PfX2 |
= j=X0 |
= ig = PfX2 |
= j; fX1 = kg=X0 = ig = |
|
|
|
[ |
|
|
|
k2E |
X
=PfX2 = j; X1 = k=X0 = ig =
k2E
X
=PfX2 = j=X1 = k; X0 = igPfX1 = k=X0 = ig =
k2E
X
=PfX2 = j=X1 = kgPfX1 = k=X0 = ig =
k2E
X
=pikpkj = [P 2]ij:
k2E
44 Глава 3. Цепи Маркова
Отсюда видно, что P (2) = P 2 , так как правая часть последнего равенства представляет собой формулу перемножения матриц. Читателю предлагается завершить доказательство самостоятельно в качестве упражнения 7.
Приведенная теорема содержит очень важное свойство марковской цепи, состоящее в том, что ее переходные вероятности обладают полугрупповым свойством.
Следствие 7.1. Семейство МВП марковской цепи за n шагов образует полугруппу:
P (n+m) = P (n)P (m) |
|
(7.6) |
|
или, в скалярной форме, |
pik(m)pkj(n) |
: |
(7.7) |
pij(m+n) = |
|||
|
X |
|
|
|
k2E |
|
|
Доказательство провести самостоятельно в качестве упражнения 8. |
|||
Именно это свойство позволяет восстанавливать все характеристики марковской цепи по ее переходной матрице. Более детально это обсуждается в разделе 7.4. Соотношения (7.6, 7.7) называются уравнением Колмогорова-Чепмена.
Рассмотрим теперь постановки некоторых других типовых задач, которые возникают при исследовании явлений и процессов, описываемых марковскими цепями. Решения этих задач приводятся в последующих параграфах.
Время непрерывного пребывания цепи (системы) в некотором множестве состояний.
В примере 2 эта величина характеризует длину серии наблюдений пробега автомобиля, расхода электроэнергии или дебита нефтяной скважины, заключенных в заданных пределах, в примерах 4 и 5 эта величина указывает время пребывания в исправных или неисправных состояниях, в модели Эренфеста для диффузии (пример 7) это может быть время, в течение которого в обеих частях сосуда находится хотя бы одна молекула; наконец в примере 8 это может быть число поколений одной семьи, выбирающих профессии из фиксированного множества типов профессий. Тесно связанной с этой является задача исследования времени достижения цепью (системой) некоторого состояния или множества состояний. В примерах 4 и 5 это может быть время безотказной работы системы, в примере 7 время до попадания всех частиц в одну часть сосуда, в примере 8 число поколений, за которое представитель семьи достигнет определенного профессионального уровня.
Вероятность попадания процесса в фиксированное состояние или множество состояний после выхода из другого множества состояний.
В примере 7 это может быть задача о типах отказов. Если провести медицинскую параллель с задачей надежности, то решение этой задачи связано с установлением причин смертности.
Доля времени, проведенного системой в том или ином состоянии или множестве состояний.
В моделях, описывающих задачи надежности (примеры 4, 5), долю времени, проводимого системой в рабочих состояниях, называют “коэффициентом готовности”. Его вычисление составляет одну из основных задач теории надежности.
Функционалы.
Наряду с исходным процессом часто приходится рассматривать некоторые числовые функционалы от его траекторий, характеризующие, например, доход от системы в процессе ее функционирования. Предположим, например, что в примере 4 за любой период времени, когда машина работает,
§ 7. Определение. Основные свойства |
45 |
она дает доход r условных единиц, а в состоянии отказа требует c условных единиц в течение одного интервала для ремонта. Доход от эксплуатации такой системы может быть представлен функционалом
X |
|
R(t) = |
r 1fX(i)=0g c 1fX(i)=1g : |
0 i t |
|
Тогда интерес может представлять изучение асимптотического поведения этих функционалов или другая связанная с ними характеристика.
Время обрыва.
Если МВП является полустохастической, то одной из задач является изучение времени существования марковской цепи, т.е. распределения времени обрыва.
В следующих главах будут предложены общие методы решения этих и других задач анализа систем, описываемых марковскими цепями.
7.4. Теорема Колмогорова
Этот параграф мы начали с предположения о том, что на некотором вероятностном пространстве задана последовательность с.в., обладающая марковским свойством. При этом в стороне остался вопрос о том, существует ли такое вероятностное пространство, на котором можно реализовать последовательность с.в., да еще обладающую наперед заданным свойством, т.е., вообще, существует ли объект, который мы изучаем, и не является ли изучаемое множество объектов пустым? Все это не праздные вопросы, и положительный ответ на них дает анонсированная в разделе 7.1. теорема Колмогорова.
Теорема 7.4 (Теорема Колмогорова). Для всякой стохастической матрицы P = [pij]i;j2E и произвольного распределения = fai; i 2 E; g можно построить вероятностное пространство и марковскую цепь на нем такую, что ее переходные вероятности и начальное распределение будут совпадать с заданными.
Доказательство проведем конструктивным методом, т.е. предъявим соответствующие объекты. Выберем в качестве множества элементарных событий = f!g множество всех последовательностей ! = (j0; j1; : : : ; jn; : : : ); где jn 2 E точки пространства состояний наблюдаемого процесса, в нашем случае просто неотрицательные целые (натуральные) числа. В качестве простых событий рассмотрим одномерные цилиндры, т.е. множества последовательностей с одной фиксированной координатой Ck(i) = f! : jk = ig: Тогда -алгебра всех наблюдаемых событий состоит из счетных объединений и пересечений простых событий. Определим вероятности цилиндров
C(0;1;:::;n)(i0; i1; : : : ; in) = f! : j0 = i0; j1 = i1; : : : ; jn = ing |
|
с фиксированными n первыми координатами формулой |
|
P C(0; 1;:::;n)(i0; i1; : : : ; in) = i0 pi0i1 : : : pin 1in ; |
(7.8) |
где = fai; i 2 Eg заданное распределение вероятностей на E, имеющее смысл начального распределения, а pij заданные вероятности переходов. Так как все события порождаются путем пересечений и объединений простых цилиндров, то построенная вероятностная мера распространяется на все конечные, а затем по теореме о продолжении меры и на все счетные объединения и пересечения цилиндров. Следовательно, для произвольного начального распределения= fai; i 2 Eg мы построили вероятностную меру P на -алгебре наблюдаемых событий.
Покажем, что случайная последовательность Xn(!), задаваемая соотношением
Xn = Xn(!) = Xn(i0; i1; : : : ; in; : : : ) = in

46 |
Глава 3. Цепи Маркова |
определяет на построенном вероятностном пространстве искомую марковскую цепь. Действительно, равенство
|
PfXn+1 = j=X0 = i0; X1 = i1; : : : ; Xn = ing = |
|||||||
= |
|
PfX0 = i0; X1 = i1; : : : ; Xn = in; Xn+1 = jg |
= |
|||||
|
|
|
PfX0 = i0; X1 = i1; : : : ; Xn = ing |
|
||||
= |
|
P C(0; 1;:::;n;n+1)(i0; i1; : : : in; j) |
= |
|
||||
|
|
ai |
pi i |
: :(0:;pi ;i |
pi ;j |
|
|
|
|
|
P |
C 1;:::;n)(i0; i1 |
; : : : ; in) |
|
|||
= |
0 0 1 |
n 1 n n |
= pin;j; |
|
||||
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
ai0 pi0i1 : : : pin 1in |
|
|
|
|||
в котором используется представление (7.8) для вероятностей цилиндрических множеств, показывает, что последовательность fXng обладает марковским свойством, а ее матрица переходных вероятностей совпадает с заданной. Из этого же равенства видно, что начальное распределение совпадает с заданным.
Приведенная теорема при заданном начальном распределении устанавливает, в некотором смысле, взаимно однозначное соответствие между множествами всех марковских цепей и стохастических матриц.
Замечание 2. Заметим, что переходную матрицу можно вычислить для любой случайной последовательности, но только предположение марковости позволяет по переходной матрице найти все конечномерные распределения, иначе говоря, найти вероятности любых событий, связанных с этой последовательностью.
Формула (7.8) определяет распределение (меру) P в пространстве траекторий (реализаций) последовательности fXng, зависящее от начального распределения . Меняя начальное распределение, мы получим семейство распределений fP g, отвечающее семейству марковских цепей или марковскому семейству, зависящему от начального распределения . В частности, выбирая в качестве начального распределение "i, сосредоточенное в состоянии i, "i = (0; :::; 1; :::; 0)0, мы определим марковскую цепь с переходными вероятностями P = [pij]i;j2E и начальным состоянием i. Распределение этой цепи обозначим через Pi = P"i .
Замечание 3. Вероятность Pi(A) есть условная вероятность события A, связанного с поведением цепи X, при условии, что X0 = i. Для событий, связанных с поведением цепи в моменты n > 0 правила работы с условными вероятностями сохраняются, если в качестве вероятностной меры рассматривать Pi . Действительно, пусть A и B события, определяемые траекторией цепи при n > 0. Тогда
P |
A |
B; X = i = |
PfA; B; X0 = ig |
= |
|
|||||
f |
j |
0 |
g |
PfB; X0 = ig |
|
|
|
|
||
|
|
|
= |
PifABg |
= P |
if |
A |
B |
: |
|
|
|
|
PifBg |
|||||||
|
|
|
|
|
|
j |
g |
|
||
Таким образом Pi(AB) = Pi(AjB)Pi(B). Этот факт неоднократно используется в дальнейшем.
Вероятностные меры P и Pi используются в дальнейшем для вычисления математических ожиданий M и Mi соответственно на пространстве траекторий.
Построенное в этом параграфе вероятностное пространство ( ; F; P) называется каноническим пространством марковской цепи, а соответствующая цепь X = fXk; k 0g, ее канонической версией. Это пространство и сама цепь полностью определяются заданием фазового пространства E марковской цепи, МВП P = [pij]i;j2E на нем и начальным распределением . Это позволяет отождествлять марковскую цепь X с ее матрицей вероятностей переходов P и начальным распределением .
§ 7. Определение. Основные свойства |
47 |
7.5.Дополнения
Вопросы для контроля.
1.Какой случайный процесс называется марковским? Как задаётся марковский процесс с дискретным множеством состояний?
2.Что такое “цепь Маркова”, как она задаётся? Какие цепи называются однородными?
3.Существует ли такое вероятностное пространство, на котором реализуется последовательность случайных величин, обладающих марковским свойством?
4.Как определить вероятность перехода марковской цепи за n шагов? Как найти вероятность перехода за n шагов из одного состояния цепи в другое?
5.Приведите собственные примеры марковских цепей.
6.Дайте определение матрицы вероятностей переходов, какими свойствами она обладает?
7.Как строится граф переходов марковской цепи?
8.Дайте определения стохастических и полустохастических матриц.
9.Приведите выражение для распределения времени непрерывного пребывания марковской цепи в отдельном состоянии.
Упражнения.
1.Докажите теорему 7.1.
2.Докажите, что все к.м.р. последовательностей с конечным множеством значений выражаются через к.м.р. вида (7.2) и приведите для них условия симметрии и согласованности.
3.5. Составьте МВП и постройте размеченные графы переходов для марковских цепей из примеров 5 7.
6.Нарисуйте граф переходов для марковской цепи из примера 8.
7.Завершите доказательство теоремы 7.3.
8.Докажите следствие 7.1.
Задачи.
1.Пусть дана последовательность н.о.р. с.в. Xn, принимающих значения +1 и -1 с равными вероятностями. Докажите, что последовательность Sn = Sn 1 + Xn образует цепь Маркова, постройте ее МВП и размеченный граф переходов.
2.Дана цепь Маркова X = fXng, задаваемая переходной матрицей
23
0a 1 a
a 0 1 a |
5 |
: |
41=3 1=3 1=3 |
|
Докажите, что последовательность Yn, определяемая формулой
Yn = |
(2; |
если |
Xn = 3; |
|
1; |
если |
Xn < 3; |
тоже образует цепь Маркова. Найдите ее переходную матрицу и постройте дл нее размеченный граф переходов.
3.Два игрока, каждый из которых имеет капитал 5 рублей, играют в “орлянку”, бросая симметричную монету и используя ставку 1 рубль. Постройте цепь Маркова, описывающую ход игры, выпишите ее переходную матрицу и нарисуйте размеченный граф переходов.
4.На столе лежит стопка из трех перенумерованных книг. С вероятностью pk из стопки берется книга с номером k и кладется сверху. Найдите матрицу переходных вероятностей марковской цепи, описывающей состояние стопки, и нарисуйте размеченный граф переходов.
5 [11]. Студент, после окончания очередного курса, с вероятностью переходит на следующий курс с вероятностью q, остается на второй год на том же курсе с вероятностью r = 1 p q отчисляется из института. Рассмотрите соответствующую цепь Маркова, постройте МВП и нарисуйте размеченный граф переходов.
48 |
Глава 3. Цепи Маркова |
6. Пусть Xn; n = 0; 1; 2; : : : н.о.р. с.в., PfXn = 0g = a, PfXn = 1g = 1 a. Выяснить, является ли цепью Маркова последовательность Yn = XnXn+1.
Библиографические замечания.
Впервые понятия марковской зависимости и марковского процесса были введены великим русским математиком А. А. Марковым (1856-1922). В настоящее время теория цепей и процессов Маркова является одним из важных разделов теории случайных процессов, которым посвящены многочисленные исследования как российских, так и зарубежных ученых.
Материал этого параграфа можно найти в любом учебнике по теории случайных процессов (см., например, [1], [8] и др.). Часть приводимых здесь примеров заимствована из книги [11]. Много интересных примеров приложения марковских цепей можно найти в книге [10].
§ 8. Классификация состояний и цепей |
49 |
§ 8. Классификация состояний и цепей
Поведение марковской цепи зависит от типов ее состояний. Так как марковская цепь полностью определяется своей переходной матрицей (см. предыдущий параграф), то классификация ее состояний и самих цепей может и должна быть проведена в терминах переходных вероятностей. Они позволяют ввести на пространстве состояний цепи некоторый естественный порядок, отвечающий ее внутренней структуре.
8.1.Классификация состояний
Пусть дана марковская цепь X = fXn; n 0g, с пространством состояний E = f0; 1; : : : Ng и МВП P = [pij]ij2E. Используя переходные вероятности марковской цепи введем на множестве ее состояний E два бинарных отношения:
(а) отношение следования i ) j и
(б) отношение связности i , j.
Определение 8.1. Будем говорить, что состояние j достижимо из состояния i и обозначать это символом i 7!j, если из состояния i можно перейти в состояние j за некоторое число шагов m, т.е. если существует m, такое что p(ijm) > 0. Состояние j следует за состоянием i (обозначение: i ) j), если состояние j достижимо из состояния i, но i не достижимо из j, т.е. если существует
m, такое что p(ijm) > 0, но что p(jin) = 0 для всех n.
Наконец, состояния i и j называются связанными или сообщающимися, что обозначается символом i , j, если они взаимно достижимы друг из друга, т.е. если существуют целые числа m; n, для которых p(ijm)p(jin) > 0.
Лемма 8.1. Отношение (а) обладает свойствами:
(i)антисимметрии: i ) j влечет отрицание j ) i,
(ii)транзитивности: i ) j и j ) k влечет i ) k;
аотношение (б) свойствами:
(i)рефлексивности: i , i,
(ii)симметричности: i , j влечет j , i,
(iii)транзитивности: i , j, j , k влечет i , k, т.е. является отношением эквивалентности.
Доказательство провести самостоятельно в качестве упражнения 1 (см. указание в разделе “Дополнения”). Следствием решения этого упражнения является утверждение о том, что отношение связности i , j является отношением эквивалентности, а отношение i ) j отношением частичного
порядка. Приведем классификацию состояний.
Определение 8.2. Состояние i называется несущественным, если существует следующее за ним состояние j, т.е. если 9 m : p(ijm) > 0, но p(jin) = 0 8 n. Все остальные состояния называются существенными. Состояние i называется поглощающим, если pii = 1.
Другими словами, несущественным является такое состояние, для которого существует достижимое из него состояние, из которого оно не достижимо, а сообщающимися являются взаимно достижимые состояния.
Так как отношение связности состояний “,” является отношением эквивалентности, то все состояния марковской цепи этим отношением эквивалентности разбиваются на непересекающиеся
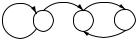
50 |
Глава 3. Цепи Маркова |
классы Ek сообщающихся состояний (см. упражнение 2). Классы существенных сообщающихся состояний называются также эргодическими классами (смысл этого названия станет ясен позже). Поглощающее состояние образует отдельный эргодический класс (см. упражнение 3).
Для некоторых марковских цепей с дискретным временем характерна периодичность посещения своих состояний. Примером такой цепи является цепь, задаваемая графом переходов, показанным на рис. 8.1.
|
|
p |
1 |
|
|
01 |
|
p |
0 |
1 |
2 |
00 |
|
|
|
|
|
|
1 |
Рис. 8.1. Пример графа переходов периодической марковской цепи.
Если эта цепь отправляется из состояния 1, то она будет возвращаться в это состояние только в нечетные моменты времени и будет находиться в состоянии 2 в четные моменты времени.
Другой пример такого рода дает рассмотренная в предыдущем параграфе модель Эренфеста для диффузии (Пример 7.7).
Определение 8.3. Состояние i называется периодическим с периодом di > 1, если возвращение в него возможно лишь за число шагов, кратное di, в противном случае состояние называется
непериодическим (апериодическим или регулярным).
Формализуем это определение. Пусть Ni - множество моментов времени, за которое возможно
возвращение в состояние i:
Ni = fn : p(iin) > 0g:
Наибольший общий делитель этих чисел, di = НОД fNig = НОД fn : p(iin) > 0g является периодом состояния i. Если di = 1, то состояние является непериодическим.
Теорема 8.1 (1-ая теорема солидарности). Все состояния одного и того же класса сообщающихся состояний имеют один и тот же период.
Доказательство. Пусть сообщающиеся состояния i, j, i , j, имеют периоды di; dj соответственно. Покажем, что di = dj. По определению сообщающихся состояний существуют числа m и n такие, что p(ijm)p(ijn) > 0. Так как
p(iim+n) p(ijm)p(jin) > 0;
то m + n нацело делится на di. Пусть теперь p(jjk) > 0 для некоторого k, т.е. k нацело делится на
dj. Тогда
p(iim+n+k) p(ijm)p(jjk)p(jin) > 0;
поэтому m + n + k нацело делится на di, а так как этим свойством обладает и число m + n, то k нацело делится на di, т.е. di dj. Аналогично показывается, что dj di, откуда следует равенство этих чисел.
Внутри периодического класса сообщающихся состояний можно провести дополнительное разбиение состояний на подклассы. С этой целью введем на периодическом классе еще одно бинарное отношение /, полагая i / j, если существует число k такое, что p(ijkd) > 0
Лемма 8.2. Отношение /
(i)симметрично, т.е. i / j влечет j / i;
(ii)рефлексивно: i / i и
