Курс_лекций_по_теории_случайных_процессов

Заметим, что если все Yk равны единице, Yk = 1, то процесс накопления Y (t) превращается в уже рассмотренный ранее процесс восстановления, Y (t) = N(t).

Покажем теперь, что процесс восстановления с неотрицательными интервалами между восстановлениями сводится к некоторому процессу накопления с положительными интервалами между ними. Пусть дана последовательность неотрицательных н.о.р. с.в. Xn с общей ф.р. F (t). Обозначим через p = F (+0) скачек ф.р. F (t) в нуле. Наличие такого скачка означает, что с вероятностью p с.в. Xn принимают значение 0 и, следовательно, в силу их независимости, процесс N(t) совершает n 1 “мгновенных” скачков с вероятностью (1 p)pn. Таким образом, процесс N(t) можно представить как процесс накопления Y (t), величина скачков которого характеризуются с.в. Yn, имеющими геометрическое распределение с параметром p = F (+0).

Примеры применения.

1.Затраты на ремонт оборудования. Если с.в. Xk представляют собой интервалы между отказами некоторого оборудования, а с.в. Yk стоимость его ремонта, то процесс Y (t) описывает затраты на ремонт оборудования в течении времени t.

2.Модель износа оборудования. Предположим, что отказ некоторого (механического) оборудования наступает в результате его износа (“усталости”), который накапливается в результате воздействия вибрации (ударов), наступающих в моменты времени Sn с величиной удара Yn. Тогда процесс Y (t) представляет собой величину накопленного износа. Исследование таких моделей представляет значительный интерес для решения вопросов планирования замен и предотвращения аварий технического оборудования.

3.Модель водохранилища. Если моменты Sn представляют собой моменты выпадения осадков в бассейне некоторого водохранилища, а величины Yn количество выпавших в момент Sn осадков, то процесс Y (t) описывает количество поступившей в водохранилище воды. Если при этом происходит (естественный, за счет испарения, или искусственный) отбор воды из водохранилища с интенсивностью c, то состояние водохранилища в момент времени t описывается процессом

где Z0 количество воды в водохранилище в некоторый начальный момент времени t0.

Такие модели использовались для описания поведения естественных водохранилищ (озер и внутренних морей), а также искусственных водохранилищ, нефтехранилищ и т.п.

4. Страховые компании. Если в предыдущей модели моменты Sn представляют собой моменты выплат страховых компенсаций (в связи с наступлением страховых событий), величины Yn представляют собой величину страховых выплат, а постоянная c имеет смысл интенсивности поступления страховых взносов (премий), то процесс

Z(t) = Z0 Y (t) + ct;

аналогичный (6.11), описывает финансовое состояние (резервы) страховой компании с начальным капиталом Z0. Изучение поведения таких процессов представляет собой одно из основных направлений исследований в страховой математике.

5. Активы финансовой компании. Если моменты Sn представляют собой моменты наблюдения активов на рынке ценных бумаг, а величины Yn приращения цены тех или иных ценных бумаг, то процесс Y (t) описывает состояние активов компании. Модели такого типа исследуются в финансовой математике.

На процессы накопления переносятся многие результаты теории процессов восстановления. Приводимые далее обобщения приводятся для случая независимых компонент вектора (Xk; Yk), так что последовательности fXk; k = 1; 2; : : : g и fYk; k = 1; 2; : : : g предполагаются взаимно независимыми с распределениями F (x) = PfXk < xg и G(y) = PfYk < yg соответственно. Заметим,

32 Глава 2. Процессы восстановления

что приводимые ниже результаты допускают обобщения на случай зависимых компонент. Однако получающиеся при этом формулы будут включать коэффициенты корреляции между компонентами вектора (Xk; Yk) и оказываются значительно сложнее. В частности, если через

p~(v; t) = Me vZ(t)

обозначить (одномерную) ПФ процесса накопления Z(t), а через

ее ПЛ, то имеет место представление (см. упражнение 3)

где f~(s) = Me sXk и g~(v) = Me vYk ПФ СВ Xk и Yk соответственно. На процессы накопления распространяются ЗБЧ и ЦПТ. Обозначим

X = MXk; Y = MYk; X2 = DXk; Y2 = DYk:

Тогда, можно показать (см. задачу 3), что

MY (t) = MN(t) Y = H(t) Y ;

DY (t) = H(t) Y2 + DN(t) 2Y :

Теорема 6.3 (ЗБЧ). Если X < 1; Y < 1, то по вероятности и с вероятностью 1 имеет

место сходимость

1Y (t) ! Y : t X

Теорема 6.4 (ЦПТ). Если X < 1; Y < 1 и, кроме того, X2 < 1; Y2 < 1, Распределение (одномерное) процесса Y (t) асимптотически нормально

89

Комментарий. Поскольку процесс накопления представляет собой сумму случайного числа N(t) н.о.р. с.в. Yn, и так как N(t) неограниченно возрастает при t ! 1, то естественно ожидать, что процесс Y (t) удовлетворяет ЗБЧ и ЦПТ. Строгое доказательство этих теорем носит технический характер и здесь не воспроизводится, его можно найти, например, в [17].

Одним из важнейших вопросов при исследовании процессов накопления является вопрос о пересечении уровня. В задаче об износе оборудования проблема пересечения уровня допустимой усталости связана с моментом наступления отказа. В модели страховой компании пересечение нулевого уровня процессом резерва означает “разорение” страховой компании. Проблема пересечения заданного уровня в моделях финансовой математики связана с изучением допустимого “уровня риска” финансовых операций.

Обозначим через Tc момент первого пересечения процессом Y (t) уровня c. Обозначим, кроме того, через q(t; c) и (y; t) плотности распределения с.в. Tc и Y (t) соответственно. Рассмотрим частный случай, когда величины Yn неотрицательны. Тогда из соотношения

fTc > tg = fY (t) < cg;

1c

ZZ

q(x; c) dx = (y; t) dy:

К сожалению, полученная “явная формула” на практике мало эффективна, так как обратное преобразование редко удается получить. Однако она позволяет получать моменты и проводить асимптотический анализ.

6.5. Регенерирующие процессы*

Тесно связанными с процессами восстановления являются так называемые регенерирующие процессы, которые находят широкое применение при решении различных прикладных задач. Рас-

смотрим случайный процесс Z = fZ(t); t 2 Rg и обозначим через FtX = fZ(s); s tg -алгебру восстанавливаемых по траекториям процесса до момента t (наблюдаемых до момента t в связи

с процессом) событий. Пусть далее fSn; n = 1; 2; : : : g последовательность моментов времени, связанных с процессом и не зависящих от его будущего, т.е. таких что

Определение 6.4. Связанный с процессом Z случайный момент времени T называется марковским моментом, если для него выполняется соотношение (6.13). Марковский момент T называется моментом регенерации процесса, если поведение процесса после этого момента не зависит от его прошлого, т.е.

Процесс называется регенерирующим, если у него существует бесконечная возрастающая последовательность fSn; n = 1; 2; : : : g моментов регенерации.

Замечание 3. Обычно моментами регенерации являются моменты попадания процесса в некоторое состояние состояние регенерации. Для процесса, заданного на всей числовой прямой, можно показать, что если у него существует хотя бы один собственный момент регенерации, то существует и целая последовательность таких моментов.

Доказательство. Так как (t; B) PfX1 tg, то, очевидно, что при t ! 1 существует предел:

0 lim (t; B) lim PfX1 tg = 0;

t!1 t!1

функция (t; B) удовлетворяют условиям узловой теоремы восстановления Смита. Поэтому существует предел

Использование дискретных процессов восстановления позволяет перенести эти результаты на дискретные регенерирующие процессы. Мы воспользуемся этими результатами в дальнейшем при исследовании марковских цепей в следующей главе и марковских и полумарковских процессов в главе 4.

6.6.Дополнения

Вопросы для контроля.

1.Дайте определения и нарисуйте траектории возраста и остаточного времени до восстановления.

2.Сформулируйте теорему о предельном распределении возраста и остаточного времени до восстановления.

3.Какими общими свойствами обладают одномерные предельные распределения возраста и остаточного времени жизни?

4.Дайте определение процесса накопления.

5.Дайте определение альтернирующего процесса восстановления.

6.Какой процесс восстановления называется стационарным и почему?

Упражнения.

1.Нарисуйте траектории процессов возраста и остаточного времени жизни.

2.Нарисуйте траектории альтернирующего процесса восстановления.

3.Докажите формулу (6.12)

4.Покажите, что для пуассоновского процесса как распределения в любой момент времени, так и предельные распределения возраста и остаточного времени до восстановления имеют показательные распределения.

5.Вычислите одномерные распределения возраста и остаточного времени до восстановления для процесса восстановления с заданными распределениями интервалов между отказами.

6.Как вычисляются соответствующие предельные распределения?

Задачи.

1. С возрастом и остаточным временем до восстановления связаны некоторые парадоксы. Очевидно, соотношение

частности, при показательном распределении интервала между восстановлениями величины Zt и Zt+ имеют то же самое показательное распределение, так что M(Zt +Zt+) = 2 . Как объяснить парадокс, связанный с этими величинами?

Указание. Следует обратить внимание на то, что случайный интервал в правой части соотношения (*) имеет случайный индекс.

2.Выведите формулу для распределения числа восстановлений дискретного процесса восстановления.

3.Вычислите математическое ожидание MY (t) и дисперсию DY (t) процесса накопления Y (t).

Глава 3.

Цепи Маркова

§ 7. Определение. Основные свойства

7.1.Определения

В этой главе мы будем предполагать, что с.п. наблюдается в дискретные моменты времени, а число его возможных значений или, что то же самое, число состояний конечно или счетно, причем начнем со случая конечного числа значений.

Значения аргумента n в последовательности наблюдений Xn могут иметь различный смысл, например времени, измеренного в некоторых единицах, расстояния, измеренного в соответствующих единицах, и т.п. В математической модели целесообразно абстрагироваться от конкретного содержания параметра n и рассматривать его просто как последовательность натуральных чисел.

Аналогично, сами наблюдения могут описывать различные физические явления, изменяющиеся во времени, пространстве или в другом процессе, измеряемые некоторыми единицами, или просто фиксирующие состояния изучаемой системы. Ввиду конечности числа значений или состояний, их можно перенумеровать и, поставив в соответствие каждому состоянию его номер, рассмотреть в качестве пространства состояний конечное множество натуральных чисел, E = f1; 2; : : : ; Ng, иногда удобнее E = f0; 1; 2; : : : ; Ng: При этом, правда, теряются некоторые “структурные” свойства процесса, связанные со структурой его фазового пространства. Однако такой подход позволяет сосредоточить внимание на принципиальных свойствах изучаемых процессов, оставляя структурные свойства для специальных исследований.

Как известно из курса теории вероятностей и было отмечено во введении, любые исследования стохастических моделей начинаются с задания вероятностного пространства, на котором соответствующая стохастическая модель может быть реализована. Мы проведем построение вероятностного пространства для цепи Маркова в разделе 7.4. Сначала приведем определение и изучим простейшие свойства таких моделей в предположении, что они рассматриваются на некотором вероятностном пространстве.

Пусть на некотором вероятностном пространстве ( ; F; P) задана последовательность X = fXn; n 0g с.в. Xn = Xn(!), принимающих значения из E = f0; 1; : : : ; Ng.

Содержательно понятие марковского процесса вводится с помощью понятия марковского свойства, которое означает независимость “будущего” от “прошлого” при известном “настоящем”. Применительно к процессам с дискретным временем (последовательностям) и дискретным множеством состояний это понятие формализуется с помощью следующего определения.

Определение 7.1. Последовательность с.в. X = fXn; n 0g со значениями из E называется

марковской последовательностью, или марковской цепью, если для любого натурального n и

любых i0; : : : ; in 1; i; j 2 E

Стоящую в правой части этого равенства вероятность назовем вероятностью переходов или переходной вероятностью марковской цепи и обозначим через

PfXn+1 = j=Xn = ig = pij(n):

В этом определении величина Xn трактуется как “настоящее”, Xn+1 как “будущее”, а fX0; X1; : : : ; Xn 1g как “прошлое”. Если Xn = i, то говорят, что марковская цепь X в момент n (на шаге n) находится в состоянии i, или что система находится в состоянии i в момент n.

Вероятности переходов зависят, вообще говоря, от трех аргументов: n; i и j. Мы будем рассматривать только такие цепи, в которых она не зависит от n, т.е. от времени. В соответствии с этим ограничением введем

Определение 7.2. Марковская цепь называется однородной, если ее переходные вероятности не зависят от параметра n, pij(n) = pij.

В дальнейшем слово “однородная” опускается, т.к. будут рассматриваться только однородные цепи, а матрицу, составленную из чисел pij обозначим через P = [pij]i;j2E и будем называть

матрицей вероятностей переходов (МВП) или переходной матрицей.

Исходя из определения переходных вероятностей выводятся их свойства.

Теорема 7.1. Переходные вероятности марковской цепи обладают следующими свойствами:

В некоторых приложениях бывает полезно рассматривать так называемые обрывающиеся марковские цепи, для которых свойство (2) нарушается и заменяется на более общее условие

Строгое неравенство для какого-нибудь состояния i в последнем соотношении означает, что с вероятностью

X

pi = 1 pij j2E

после выхода из состояния i цепь исчезает (покидает рассматриваемое множество состояний E), т.е. время существования цепи случайно. К исследованию и применениям таких цепей мы возвратимся в § 9

Определение 7.3. Матрица, элементы которой удовлетворяют условиям (1) и (2) называется стохастической матрицей, а матрица, удовлетворяющая условиям (1) и (2а) полустохастической.

Вычислим теперь к.м.р. марковской цепи и покажем, что они выражаются через ее МВП и дополнительную информацию о ее начальном распределении

ai = PfX0 = ig; i 2 E:

Заметим предварительно, что при вычислении к.м.р. последовательностей с конечным множеством значений достаточно ограничиться выражениями вида (см. упражнение 2)

Теорема 7.2. К.м.р. марковской цепи определяются через переходные вероятности [pij]i;j2E и начальное распределение = fai; i 2 Eg формулой

1 j n

Доказательство. Используя формулу условных вероятностей, марковское свойство и простую индукцию имеем

p(k0; k1; : : : ; kn) = PfXi = ki; i = 0; ng =

=PfXn = kn=Xi = ki; i = 0; n 1gPfXi = ki; i = 0; n 1g = : : :

=pkn 1kn pkn 2kn 1 : : : pk0k1 a0:

Из сказанного выше следует, что к.м.р. марковской цепи выражаются через ее МВП, которая является стохастической матрицей. В дальнейшем в разделе 7.4. будет доказано обратное утверждение о том, что всякая стохастическая матрица P = [pij]i;j2E наряду с начальным распределением = fai; i 2 Eg однозначно определяют марковскую цепь такую, что ее переходные вероятности и начальное распределение совпадают с заданными.

Наряду с матрицей вероятностей переходов марковскую цепь удобно представлять с помощью ориентированного размеченного графа, называемого графом переходов, вершинами которого являются состояния, или значения наблюдаемого процесса, а дуги указывают возможные изменения состояний, т.е. соединяют те вершины, для которых pij > 0. Величины pij являются метками соответствующих дуг. На рис.7.1 в качестве примера 1 приведен граф переходов марковской цепи c МВП.

Пример 1.

23

Рис. 7.1. Размеченный граф переходов марковской цепи с МВП P .

Ясно, что по всякой стохастической матрице можно построить соответствующий граф переходов и наоборот. Таким образом, наряду с МВП марковскую цепь можно задавать ее размеченным графом переходов.

7.2.Примеры.

Рассмотрим несколько примеров моделирования явлений с помощью цепей Маркова.

Пример 2. Измерения различных величин (пробега автомобиля, дебита нефтяной или газовой скважины, расхода электроэнергии каким-либо потребителем) X = fXn; n = 1; 2; : : : g за отдельные промежутки времени часто можно рассматривать как н.о.р. с.в. с конечным числом возможных значений, скажем, в пределах от 0 до N с вероятностями

PfXn = kg = pk; k = 0; : : : ; N:

Рис. 7.2. Полносвязный размеченный граф переходов марковской цепи из примера 2.

Такую последовательность fXng можно рассматривать также как марковскую цепь с пространством состояний E = f0; 1; : : : ; Ng, переходными вероятностями pij = pj; i; j 2 E, и МВП

23

При этом совпадение строк матрицы указывает на независимость с.в. Xn. Граф переходов этой цепи является полносвязным графом, в котором каждая вершина соединена с любой другой. Он представлен на рис. 7.2.

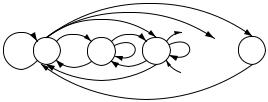
Пример 3. (Продолжение). Если рассматривать накопленные за n дней измерения (пробег автомобиля, суммарный расход электроэнергии, или дебит скважины): Sn = Xn + + Xn, то множество значений этих величин не ограничено, так как Sn принимает значения в интервале [0; nN]. Примеры такого рода описываются марковскими цепями со счетным множеством состояний (см. § 11).Тем не менее, последовательность fSng образует цепь Маркова с переходными вероятностями

Ее матрица вероятностей перехода может быть представлена бесконечной вниз и вправо таблицей, но чтобы не выходить за рамки конечных моделей, рассматриваемых в настоящем разделе, будем считать, что по достижении некоторого состояния, скажем M, процесс возвращается в состояние 0. Применительно к пробегу автомобиля это означает, что фактически наблюдается не пробег автомобиля, а показания спидометра, которые “обнуляются” по достижении пробега в M = 100000 км.

МВП размерности M M для такой цепи имеет вид

а граф переходов показан на рис. 7.3

Пример 4. Рассмотрим некоторое техническое устройство (например автомобиль), которое может находиться в двух состояниях исправном и неисправном. Наблюдения за процессом функционирования устройства в дискретные моменты времени с некоторым фиксированным интервалом времени можно описать последовательностью, принимающей два значения, скажем 0, если устройство исправно и 1, если оно неисправно.

Предположим, что переход из исправного состояния в неисправное происходит с вероятностью p независимо от предыдущей истории, а с дополнительной вероятностью 1 p также независимо от предыдущей истории устройство остается в исправном состоянии в течение следующей единицы