
- •Глава 7. Основы теории информации
- •7.1. Информационные характеристики источников сообщений
- •7.1.1. Определение количества информации
- •, (7.1)
- •Определение количества информации по к. Шеннону
- •Энтропия сообщения. Среднее количество информации по всем состояниям системы:
- •7.1.2. Информационные характеристики источников дискретных сообщений
- •Измеряется производительность источника в единицах измерения информации, отнесенных к единице времени - секунде.
- •7.1.3. Информационные характеристики источников непрерывных сообщений
- •7.2. Информационные характеристики каналов электросвязи
- •7.2.1. Вероятностные модели каналов связи в теории информации
- •7.2.2. Информационные характеристики каналов связи Информация
- •7.2.4. Обменность канальных ресурсов
Измеряется производительность источника в единицах измерения информации, отнесенных к единице времени - секунде.
С точки зрения передачи информации, производительностью источника называют среднее количество информации, выдаваемой источником в единицу времени.
Таким образом, знание информационных характеристик источников сообщений, умение их определять позволяет сравнивать между собой различные источники сообщений и обосновывать требования, предъявляемые к каналам передачи информации.
7.1.3. Информационные характеристики источников непрерывных сообщений
Основные информационные характеристики источников непрерывных сообщений следующие: дифференциальная энтропия, эпсилон-энтропия, эпсилон-производительность, избыточность, объем информации.
Дифференциальная энтропия.
Аналитическое
выражение для энтропии источника
непрерывных сообщений получают путем
предельного перехода из формулы для
энтропии дискретного источника
![]() .
.
Рис.
7.4 Вероятность того, что
интервале
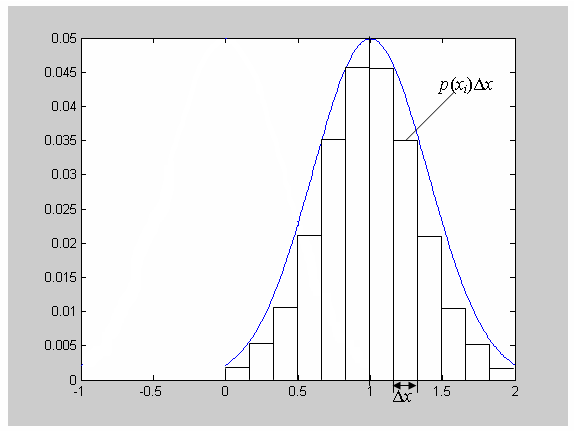
![]() будет находиться в
будет находиться в![]() ,
равна
,
равна
![]()
Если
одномерная плотность распределения
случайного стационарного процесса
![]() равна
равна![]() ,
то вероятность того, что
,
то вероятность того, что![]() будет находиться в интервале
будет находиться в интервале![]() ,
равна
,
равна![]() (рис.7.4).
(рис.7.4).
Если
всего интервалов квантования
![]() ,
то энтропия источника непрерывных
сообщений
,
то энтропия источника непрерывных
сообщений
![]() .
(7.11)
.
(7.11)
.В
результате предельного перехода при
![]() получим
получим
![]() . (7.12)
. (7.12)
Первую составляющую (7.12)
![]() (7.13)
(7.13)
называют
дифференциальной
энтропией источника
непрерывных
сообщений. Вторая составляющая
![]()
![]() и показывает, что энтропия источника
непрерывных сообщений стремится к
бесконечности.
и показывает, что энтропия источника
непрерывных сообщений стремится к
бесконечности.
Скорость
передачи информации, пропускную
способность и другие основные
информационные характеристики источников
определяют через разность энтропии.
Поэтому вторая составляющая в этих
операциях сокращается и величиной
![]() можно характеризовать информационные
свойства источников непрерывных
сообщений. В отличие от энтропии
источников дискретных сообщений
можно характеризовать информационные
свойства источников непрерывных
сообщений. В отличие от энтропии
источников дискретных сообщений![]() может принимать положительные,
отрицательные и нулевые значения.
Величина
может принимать положительные,
отрицательные и нулевые значения.
Величина![]() изменяется при изменении масштаба
измерения
изменяется при изменении масштаба
измерения![]() .
.
Определим
дифференциальную энтропию для сигнала
![]() с плотностью распределения
с плотностью распределения
![]() ,
,
где
![]() - математическое ожидание,
- математическое ожидание,![]() - дисперсия.
- дисперсия.

По
определению первый интеграл
![]() .
А второй интегралравен
дисперсии
.
А второй интегралравен
дисперсии
![]() .
.
Поэтому
![]() .
(7.14)
.
(7.14)
Эпсилон-энтропия источников.
Реальная чувствительность приемных устройств органов чувств человека и разрешающая способность различных информационных измерительных систем ограничены. Поэтому воспроизводить непрерывные сообщения абсолютно точно не требуется. Наличие помех и искажений сигналов в реальных каналах делает точное воспроизведение сообщений невозможным. Поэтому вводят понятия эпсилон-энтропии.
Эпсилон-энтропия
– это то среднее количество информации
в одном независимом отсчете непрерывного
случайного процесса
![]() ,
которое необходимо для воспроизведения
этого сигнала с заданной среднеквадратической
погрешностью
,
которое необходимо для воспроизведения
этого сигнала с заданной среднеквадратической
погрешностью
![]() .
.
Среднее
количество принятой информации можно
определить как разность дифференциальной
энтропии источника
непрерывных
сообщений![]() и информации
и информации
![]() ,
потерянной
из-за шумов квантования.
,
потерянной
из-за шумов квантования.
Эпсилон-энтропия
– это то минимальное среднее количество
информации ![]() ,
которое позволяет считать
,
которое позволяет считать
![]() и
и![]() «похожими» в среднеквадратическом
смысле:
«похожими» в среднеквадратическом
смысле:
![]() ,
,
![]() достигается
при нормальном распределении, тогда
достигается
при нормальном распределении, тогда
![]() -условная энтропия,
где
-условная энтропия,
где ![]() –
математическое ожидание квадрата
значения аддитивной помехи (шума
квантования).
–
математическое ожидание квадрата
значения аддитивной помехи (шума
квантования).
Тогда эпсилон-энтропиябудет равна:
![]() .
(7.15)
.
(7.15)
Если
непрерывный случайный процесс
![]() распределен по нормальному закону, тодифференциальная
энтропия источника
непрерывных
сообщений
распределен по нормальному закону, тодифференциальная
энтропия источника
непрерывных
сообщений
![]() .
.
Эпсилон-энтропия такого источника
 .
(7.16)
.
(7.16)
Эпсилон-производительность источника. Данная информационная характеристика источника непрерывных сообщений определяется следующим выражением:
![]() [бит/с],
(7.17)
[бит/с],
(7.17)
где
![]() – максимальная частота сигнала X(t).
– максимальная частота сигнала X(t).
За
время
![]() существования сигнала максимальныйобъем
информации,
выданный источником,
существования сигнала максимальныйобъем
информации,
выданный источником,
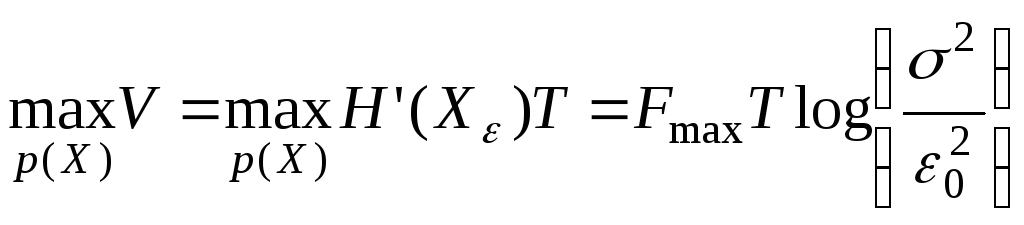 ,
(7.18)
,
(7.18)
где
![]() - дисперсия сигнала
- дисперсия сигнала![]() ,
распределенного по нормальному
закону. Поэтому объем сигнала является
одновременно экстремальной информационной
характеристикой сигнала.Объем
сигнала – это
максимальное количество информации,
которое сигнал может переносить.
,
распределенного по нормальному
закону. Поэтому объем сигнала является
одновременно экстремальной информационной
характеристикой сигнала.Объем
сигнала – это
максимальное количество информации,
которое сигнал может переносить.
Избыточность источника непрерывных сигналов определяют так же, как и для источника дискретных сигналов:
![]() .
(7.19)
.
(7.19)
Таким образом, основными информационными характеристиками источников непрерывных сообщений являются: энтропия, условная энтропия, эпсилон-энтропия, эпсилон-производительность, избыточность, объем информации, аналитические выражения которых определяются через значения характеристик одномерной плотности распределения случайного стационарного процесса.
