
- •Глава 7. Основы теории информации
- •7.1. Информационные характеристики источников сообщений
- •7.1.1. Определение количества информации
- •, (7.1)
- •Определение количества информации по к. Шеннону
- •Энтропия сообщения. Среднее количество информации по всем состояниям системы:
- •7.1.2. Информационные характеристики источников дискретных сообщений
- •Измеряется производительность источника в единицах измерения информации, отнесенных к единице времени - секунде.
- •7.1.3. Информационные характеристики источников непрерывных сообщений
- •7.2. Информационные характеристики каналов электросвязи
- •7.2.1. Вероятностные модели каналов связи в теории информации
- •7.2.2. Информационные характеристики каналов связи Информация
- •7.2.4. Обменность канальных ресурсов
Определение количества информации по к. Шеннону
Статистическая мера рассматривает информацию как исход случайных событий. Количество информации ставится в зависимость от априорных вероятностей этих событий.
Пусть
некоторая физическая система
характеризуется N
состояниями
![]() ,
,![]() ,
,![]() ,…,
,…,![]() и распределением
вероятностей этих состояний
и распределением
вероятностей этих состояний
![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
образующих полную группу несовместимых
событий т.е.:
,
образующих полную группу несовместимых
событий т.е.:
![]() .
.
Американский ученый Клод Шеннон в середине 40-х годов прошлого столетия предложил оценивать количество информации в каждом исходе мерой:
![]() .
(7.5)
.
(7.5)
За
количественную
меру информации
![]() содержащуюся в некотором сообщении
содержащуюся в некотором сообщении![]() принимается минус логарифм вероятности
этого сообщения
принимается минус логарифм вероятности
этого сообщения![]() .
.
При
![]()
![]() ,
[бит]. (7.6)
,
[бит]. (7.6)
Энтропия сообщения. Среднее количество информации по всем состояниям системы:
![]() (7.7)
(7.7)
где
![]() -энтропия
системы.
-энтропия
системы.
Функция Н была выбрана Шенноном так, чтобы она удовлетворяла следующим требованиям:
1.
![]() должна быть непрерывной относительно
должна быть непрерывной относительно
![]() .
.
2.
Если все
![]() равны,
равны,![]() ,
тоН
должна быть монотонно возрастающей
функцией от N.
В случае равновероятных событий имеется
больше возможностей выбора или
неопределенности, чем в случае, когда
имеются не равновероятные события.
,
тоН
должна быть монотонно возрастающей
функцией от N.
В случае равновероятных событий имеется
больше возможностей выбора или
неопределенности, чем в случае, когда
имеются не равновероятные события.
3.
Если бы выбор распадался на два
последовательных выбора, то первоначальная
![]() должна была бы быть взвешенной суммой
индивидуальных значений
должна была бы быть взвешенной суммой
индивидуальных значений
![]() .
.
Шенноном доказано, что существует единственная функция Н, вид которой приведен выше, удовлетворяющая этим трем требованиям. Кроме того, энтропия H характеризуется следующими свойствами:
энтропия всегда неотрицательна, так как значения вероятностей выражаются дробными величинами, а их логарифмы - отрицательными величинами, т.е. члены
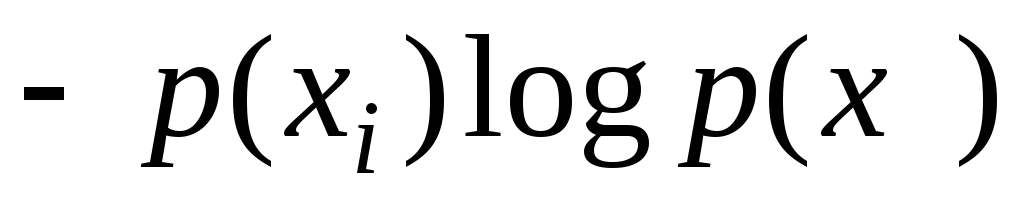 - неотрицательны;
- неотрицательны;энтропия равна нулю в том крайнем случае, когда вероятность одного события равна единице, а вероятности всех остальных нулю. Это тот случай, когда об опыте или величине все известно заранее и результат не приносит никакой новой информации;
энтропия имеет наибольшее значение при условии, когда все вероятности равны между собой
 =
=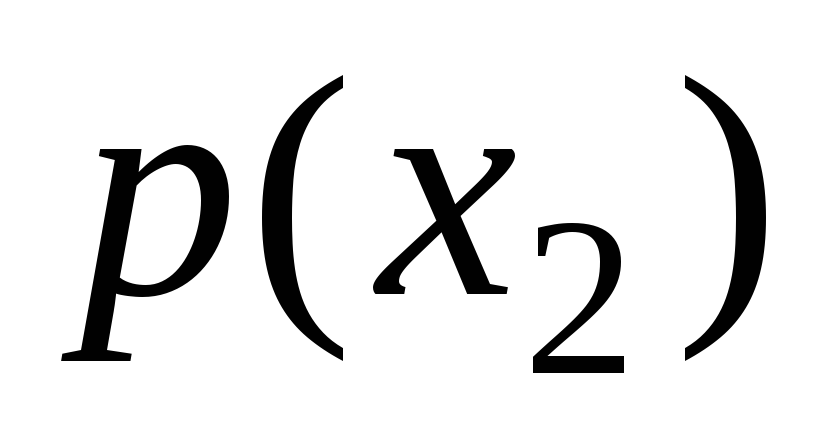 =
=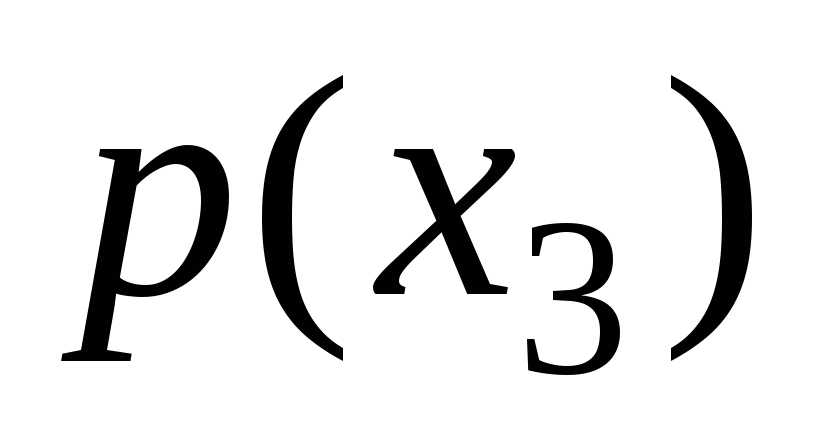 =…=
=…= =
= .
При этом
.
При этом
 .
.
Таким образом, в случае равновероятности событий статистическое определение количества информации по Шеннону совпадает с определением количества информации по Хартли. Совпадение оценок свидетельствует о полном использовании информационной емкости системы, т.e. формула Хартли соответствует максимальному значению энтропии.

Физически это определяет случай, когда неопределенность настолько велика, что прогнозировать оказывается трудно.
В случае неравенства вероятностей количество информации по Шеннону меньше информационной емкости системы.
Так энтропия для двух неравновероятных состояний одного элемента равна
![]() .
.
Поведение этой функции в зависимости от значений р1 и р2 показано на рис.7.3.
Максимум Н=1 достигается при р1=р2=0,5, когда два состояния равновероятны. При р1=1, р2=0 и при р1=0, р2=1, что соответствует полной достоверности события, энтропия равна нулю.
Кроме неравновероятности
появления символов следует учитывать,
что реальные источники вырабатывают
слова при наличии статистической
зависимости между буквами. В реальных
источниках вероятность выбора какой-либо
очередной буквы зависит от всех
предшествующих букв. Многие реальные
источники достаточно хорошо описываются
марковскими моделями источника
сообщений. Согласно указанной модели
условная вероятность выбора источником
очередной
![]() ,
буквы зависит только от
,
буквы зависит только от
![]() предшествующих букв.
предшествующих букв.
Рассмотрим
ансамбли
![]() и
и
![]() и их произведение
и их произведение
![]() .
Для любого
фиксированного
.
Для любого
фиксированного
![]() можно
построить условное распределение
вероятностей
можно
построить условное распределение
вероятностей
![]() на множестве
на множестве
![]() и для каждого
и для каждого
![]() подсчитать
информацию
подсчитать
информацию
![]() ,
,
называемую
условной
собственной информацией
сообщения
![]() - при фиксированном
- при фиксированном
![]() ,
,
Ранее
мы назвали энтропией ансамбля
![]() среднюю
информацию сообщений
среднюю
информацию сообщений
![]() .
Аналогично,
усреднив условную информацию
.
Аналогично,
усреднив условную информацию
![]() по
по
![]() ,
получим
величину
,
получим
величину
![]() ,
,
называемую
частной
условной
энтропией
X
при
фиксированном
![]() .
.
Вновь
введенная энтропия
![]() — случайная
величина, поскольку она зависит от
случайной переменной
— случайная
величина, поскольку она зависит от
случайной переменной
![]() .
Чтобы
получить неслучайную информационную
характеристику пары вероятностных
ансамблей, нужно выполнить усреднение
по всем значениям
.
Чтобы
получить неслучайную информационную
характеристику пары вероятностных
ансамблей, нужно выполнить усреднение
по всем значениям
![]() .
Величина
.
Величина
![]()
называется
условной
энтропией
ансамбля
![]() при фиксированном ансамбле
при фиксированном ансамбле
![]() .
.
Отметим ряд свойств условной энтропии:
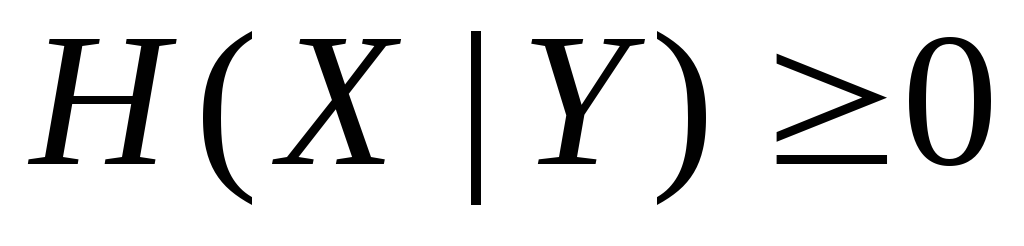 .
. ,
причем равенство имеет место в том и
только в том случае, когда ансамбли
,
причем равенство имеет место в том и
только в том случае, когда ансамбли
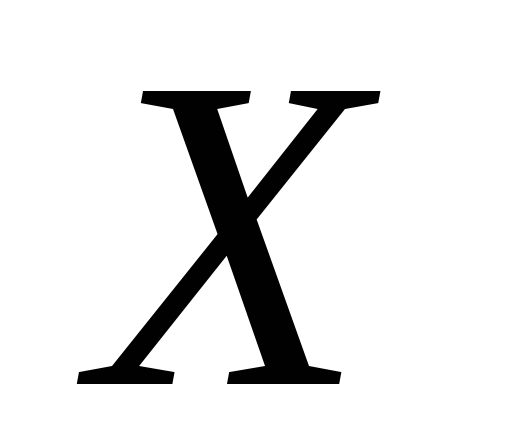 и
и
 независимы.
независимы.
3. Совместная энтропия
![]()
4.![]()
5.
![]() ,
причем равенство
имеет место в том и только в том случае,
когда ансамбли
,
причем равенство
имеет место в том и только в том случае,
когда ансамбли
![]() и
и
![]() условно независимы при всех
условно независимы при всех
![]() .
.
Обсудим
физический смысл сформулированных
свойств условной энтропии. Свойство
2 устанавливает, что условная энтропия
ансамбля не превышает его безусловной
энтропии. Свойство 5 усиливает это
утверждение. Из него следует, что условная
энтропия не увеличивается с увеличением
числа условий. Оба эти факта не удивительны,
они отражают то обстоятельство, что
дополнительная информация об ансамбле
![]() ,
содержащаяся
в сообщениях других ансамблей, в
среднем
уменьшает
информативность (неопределенность)
ансамбля
,
содержащаяся
в сообщениях других ансамблей, в
среднем
уменьшает
информативность (неопределенность)
ансамбля
![]() .
.
Из свойств 1-5 следует неравенство
![]() ,
,
в
котором равенство возможно только в
случае совместной независимости
ансамблей
![]() .
.
Напомним, что
вычисление энтропии — это определение
затрат на передачу или хранение букв
источника. Свойства условной энтропии
подсказывают, что при передаче буквы
![]() следует
использовать то обстоятельство, что
предыдущие буквы
следует
использовать то обстоятельство, что
предыдущие буквы
![]() уже известны на приемной стороне. Это
позволит вместо
уже известны на приемной стороне. Это
позволит вместо
![]() бит потратить меньшее количество
бит потратить меньшее количество
![]() бит.
бит.
