
OPR0735
.pdf
йинадД а лиЦднкйлдйиаь, 2004, ЪУП 96, ‹ 5, Т. 735–746
н ВЪЛИ ТВПЛМ‡ Ф‡ПflЪЛ С.з. дО˚¯НУ
ìÑä 530.145 (0.75.8)
йТМУ‚М˚В ФУМflЪЛfl НО‡ТТЛ˜ВТНУИ Л Н‚‡МЪУ‚УИ ТЪ‡ЪЛТЪЛНЛ: НУ МВ‚УИ ФУ‰ıУ‰
© 2004 „. û. à. ÅÓ„‰‡ÌÓ‚
йЪН ˚ЪУВ ‡НˆЛУМВ МУВ У·˘ВТЪ‚У “ДМ„ТЪ ВП”, 124460 еУТН‚‡, кУТТЛfl
E-mail: bogdanov@angstrem.ru
иУТЪЫФЛО‡ ‚ кВ‰‡НˆЛ˛ 17.07.2003 „.
к‡ТТПУЪ ВМ МУ‚˚И ПВЪУ‰ В¯ВМЛfl НО‡ТТЛ˜ВТНЛı Л Н‚‡МЪУ‚˚ı Б‡‰‡˜ ‡М‡ОЛБ‡ ‰‡ММ˚ı, УТМУ‚‡ММ˚И М‡ ТЛП·ЛУБВ Ф В‰ТЪ‡‚ОВМЛИ Н‚‡МЪУ‚УИ ЪВУ ЛЛ Л П‡ЪВП‡ЪЛ˜ВТНУИ ТЪ‡ЪЛТЪЛНЛ. йТУ·УВ ‚МЛП‡МЛВ Ы‰ВОВМУ ТФВˆЛЩЛ˜МУТЪЛ Н‚‡МЪУ‚˚ı Б‡‰‡˜, У·ЫТОУ‚ОВММУИ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ПЛ (ФУ ЕУ Ы) ЛБПВ ВМЛ-
flПЛ, НУ„‰‡, М‡Ф ЛПВ , Ф УТЪ ‡МТЪ‚ВММУ-‚ ВПВММ‡fl Н‡ ЪЛМ‡ ‰УФУОМflВЪТfl ЛПФЫО¸ТМУ-˝МВ „ВЪЛ˜ВТ-
НУИ. аБЫ˜ВМ‡ ‚УБПУКМУТЪ¸ ФУТЪ УВМЛfl ПМУ„УФ‡ ‡ПВЪ Л˜ВТНЛı ТЪ‡ЪЛТЪЛ˜ВТНЛı ПУ‰ВОВИ, ‰УФЫТН‡˛- ˘Лı ЫТЪУИ˜Л‚УВ ‚УТТЪ‡МУ‚ОВМЛВ Ф‡ ‡ПВЪ У‚ ФУ М‡·О˛‰ВМЛflП (У· ‡ЪМ‡fl Б‡‰‡˜‡ ТЪ‡ЪЛТЪЛНЛ). и Л ˝ЪУП В‰ЛМТЪ‚ВММУИ ЫМЛ‚В Т‡О¸МУИ ПУ‰ВО¸˛ Ъ‡НУ„У У‰‡ УН‡Б˚‚‡ВЪТfl НУ МВ‚‡fl ПУ‰ВО¸, УТМУ‚‡ММ‡fl М‡ Ф В‰ТЪ‡‚ОВМЛЛ ФОУЪМУТЪЛ ‚В УflЪМУТЪЛ Н‡Н Н‚‡‰ ‡Ъ‡ ПУ‰ЫОfl МВНУЪУ УИ ЩЫМНˆЛЛ (М‡Б˚‚‡ВПУИ
ФТЛ-ЩЫМНˆЛВИ ФУ ‡М‡ОУ„ЛЛ Т Н‚‡МЪУ‚УИ ПВı‡МЛНУИ). иТЛ-ЩЫМНˆЛfl Ф В‰ТЪ‡‚ОflВЪТfl ‚ ‚Л‰В ‡БОУКВ-
МЛfl ФУ У ЪУМУ ПЛ У‚‡ММУПЫ ·‡БЛТЫ Т УˆВМНУИ НУ˝ЩЩЛˆЛВМЪУ‚ ‡БОУКВМЛfl ПВЪУ‰УП П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl. дУ МВ‚УИ ФУ‰ıУ‰ ФУБ‚УОflВЪ Ф В‰ТЪ‡‚ЛЪ¸ П‡Ъ ЛˆЫ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡, П‡Ъ ЛˆЫ НУ‚‡ Л‡ˆЛИ Л ТЪ‡ЪЛТЪЛ˜ВТНЛВ Т‚УИТЪ‚‡ УˆВМУН ‚УТТЪ‡М‡‚ОЛ‚‡ВП˚ı ТУТЪУflМЛИ ‚ М‡Л·УОВВ Ф УТЪУП Л
ЫМЛ‚В Т‡О¸МУП ‚Л‰В. ь‚ОflflТ¸ ‡ТЛПФЪУЪЛ˜ВТНЛ ˝ЩЩВНЪЛ‚М˚П, ПВЪУ‰ ФУБ‚УОflВЪ ‚УТТЪ‡МУ‚ЛЪ¸ ТУТЪУ-
flМЛfl Т ЪУ˜МУТЪ¸˛, ·ОЛБНУИ Н Ф ЛМˆЛФЛ‡О¸МУ ‰УТЪЛКЛПУИ. иУН‡Б‡МУ, ˜ЪУ Ъ В·У‚‡МЛВ НУ МВ‚У„У ı‡-
‡НЪВ ‡ ‡БОУКВМЛfl ПУКВЪ ‡ТТП‡Ъ Л‚‡Ъ¸Тfl Н‡Н ЫТОУ‚ЛВ Н‚‡МЪУ‚‡МЛfl, ФУБ‚УОfl˛˘ВВ ЛБ ‚ТВı ТЪ‡ЪЛ-
ТЪЛ˜ВТНЛı ПУ‰ВОВИ, У·ВТФВ˜Л‚‡˛˘Лı ‚˚ФУОМВМЛВ ‚ Т В‰МВП Б‡НУМУ‚ НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ, ‚˚‰В- ОЛЪ¸ ТЛТЪВП˚, УФЛТ˚‚‡ВП˚В Н‚‡МЪУ‚УИ ПВı‡МЛНУИ.
ǂ‰ÂÌËÂ
д‡Н ЛБ‚ВТЪМУ, ФТЛ-ЩЫМНˆЛfl fl‚ОflВЪТfl УТМУ‚М˚П У·˙ВНЪУП Н‚‡МЪУ‚УИ ЪВУ ЛЛ, ФУТНУО¸НЫ ВВ Б‡‰‡- МЛВ ФУОМУТЪ¸˛ УФ В‰ВОflВЪ ТУТЪУflМЛВ Н‚‡МЪУ‚УИ ТЛТЪВП˚. З Б‡‚ЛТЛПУТЪЛ УЪ НУМЪВНТЪ‡ ‡ТТП‡Ъ Л- ‚‡ВП˚ı Б‡‰‡˜ ЛТФУО¸БЫ˛Ъ Л ‰ Ы„ЛВ ˝Н‚Л‚‡ОВМЪ- М˚В ЪВ ПЛМ˚: ‚УОМУ‚‡fl ЩЫМНˆЛfl, ‚ВНЪУ ТУТЪУflМЛfl, ‡ПФОЛЪЫ‰‡ ‚В УflЪМУТЪВИ. иТЛ-ЩЫМНˆЛfl ·˚О‡ ‚‚В‰ВМ‡ ‚ Ъ‡Н М‡Б˚‚‡ВПУИ ‚УОМУ‚УИ ПВı‡МЛНВ (‰В Е УИО¸, т В‰ЛМ„В ). ЗВ УflЪМУТЪМ‡fl ЛМЪВ Ф ВЪ‡- ˆЛfl, ТУ„О‡ТМУ НУЪУ УИ Н‚‡‰ ‡Ъ ПУ‰ЫОfl ФТЛ-ЩЫМН- ˆЛЛ ı‡ ‡НЪВ ЛБЫВЪ ‚В УflЪМУТЪ¸ ЛОЛ ФОУЪМУТЪ¸ ‚В-УflЪМУТЪЛ, ·˚О‡ ‰‡М‡ ЕУ МУП.
з‡ ‚ТВП Ф УЪflКВМЛЛ ЛТЪУ ЛЛ ‡Б‚ЛЪЛfl Н‚‡МЪУ- ‚УИ ЩЛБЛНЛ Т‡ПУ ФУМflЪЛВ ФТЛ-ЩЫМНˆЛЛ Н‡Н УТМУ‚- МУ„У У·˙ВНЪ‡ Н‚‡МЪУ‚УИ ЪВУ ЛЛ МВУ‰МУН ‡ЪМУ ФУ‰‚В „‡ОУТ¸ ТЫ У‚УИ Н ЛЪЛНВ. З Н‡˜ВТЪ‚В ¯Л У- НУ ЛБ‚ВТЪМ˚ı Ф ЛПВ У‚ ПУКМУ М‡Б‚‡Ъ¸ ЪВУ Л˛ ‚УОМ˚-ФЛОУЪ‡ Л ‰‚УИМУ„У В¯ВМЛfl (‰В Е УИО¸ [1]), ФУФ˚ЪНЫ ЕУП‡ ЛМЪВ Ф ВЪЛ У‚‡Ъ¸ Н‚‡МЪУ‚Ы˛ ПВı‡МЛНЫ М‡ УТМУ‚В Ф В‰ТЪ‡‚ОВМЛfl У “ТН ˚Ъ˚ı Ф‡ ‡ПВЪ ‡ı” [2], ТУПМВМЛfl щИМ¯ЪВИМ‡ УЪМУТЛЪВО¸МУ ФУОМУЪ˚ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ [3], В„У БМ‡- ПВМЛЪЫ˛ ‰ЛТНЫТТЛ˛ Т ЕУ УП [4].
е˚ТО¸ “ЛБ„М‡Ъ¸” ФТЛ-ЩЫМНˆЛ˛ ЛБ ЪВУ ЛЛ Н‡Б‡- О‡Т¸ (Л ‰У ТЛı ФУ Н‡КВЪТfl) ТУ·О‡БМЛЪВО¸МУИ ‰Оfl ПМУ„Лı ‡‚ЪУ У‚. иТЛıУОУ„Л˜ВТН‡fl ФУ‰УФОВН‡ ˝ЪУ- „У fl‚ОВМЛfl Б‡НО˛˜‡ВЪТfl, ‚Л‰ЛПУ, ‚ ЪУП, ˜ЪУ НО‡ТТЛ-
˜ВТНЛВ (‰УН‚‡МЪУ‚˚В) ЪВУ ВЪЛНУ-‚В УflЪМУТЪМ˚В Ф В‰ТЪ‡‚ОВМЛfl, УТМУ‚‡ММ˚В М‡ “М‡·О˛‰‡ВП˚ı” ‚В-УflЪМУТЪflı Л ФОУЪМУТЪflı ‚В УflЪМУТЪВИ, Н‡КЫЪТfl flТМ˚ПЛ Л М‡„Оfl‰М˚ПЛ. З ЪУ КВ ‚ ВПfl МУ‚˚В Н‚‡М- ЪУ‚˚В Ф В‰ТЪ‡‚ОВМЛfl, УТМУ‚‡ММ˚В М‡ “МВМ‡·О˛‰‡- ВП˚ı” НУПФОВНТМ˚ı ‚ВНЪУ ‡ı ТУТЪУflМЛИ ‚ „ЛО¸- ·В ЪУ‚УП Ф УТЪ ‡МТЪ‚В, Н‡КЫЪТfl ПМУ„ЛП ТОЛ¯НУП ‡·ТЪ ‡НЪМ˚ПЛ Л “МВВТЪВТЪ‚ВММ˚ПЛ”. йЪТ˛‰‡, ‚Л- ‰ЛПУ, Л Ф УЛТЪВН‡˛Ъ ПМУ„У˜ЛТОВММ˚В ФУФ˚ЪНЛ УФ У‚В КВМЛfl Ф ЛМflЪУИ ЛМЪВ Ф ВЪ‡ˆЛЛ Н‚‡МЪУ- ‚УИ ПВı‡МЛНЛ, ФУФ˚ЪНЛ ВВ Б‡ПВМ˚ МВНУЪУ УИ “Н‡- ЫБ‡О¸МУИ” ЛМЪВ Ф ВЪ‡ˆЛВИ, НУЪУ ‡fl УТМУ‚˚‚‡О‡Т¸ ·˚ М‡ НО‡ТТЛ˜ВТНЛı Ф В‰ТЪ‡‚ОВМЛflı У ‚В УflЪМУТЪЛ Л ТЪ‡ЪЛТЪЛ˜ВТНЛı Б‡НУМУПВ МУТЪflı.
䂇МЪУ‚‡fl ПВı‡МЛН‡ МВТУПМВММУ fl‚ОflВЪТfl ТЪ‡- ЪЛТЪЛ˜ВТНУИ ЪВУ ЛВИ. З ЪУ КВ ‚ ВПfl ВВ П‡ЪВП‡ЪЛ- ˜ВТНЛИ ‡ФФ‡ ‡Ъ ЛПВВЪ У˜ВМ¸ П‡ОУ У·˘В„У Т Ъ‡НЛПЛ Ъ ‡‰ЛˆЛУММУ ТЪ‡ЪЛТЪЛ˜ВТНЛПЛ М‡Ы˜М˚ПЛ М‡Ф ‡‚- ОВМЛflПЛ, Н‡Н ЪВУ Лfl ‚В УflЪМУТЪВИ, П‡ЪВП‡ЪЛ˜ВТ- Н‡fl ТЪ‡ЪЛТЪЛН‡, ЪВУ Лfl ТОЫ˜‡ИМ˚ı Ф УˆВТТУ‚ Л НО‡ТТЛ˜ВТН‡fl ТЪ‡ЪЛТЪЛ˜ВТН‡fl ЩЛБЛН‡. щЪУ У·ТЪУflЪВО¸ТЪ‚У, УЪПВ˜ВММУВ В˘В М‡ Б‡ В Н‚‡МЪУ‚УИ ЪВУ-ЛЛ, ТОЫКЛОУ ФУ‚У‰УП ‰Оfl ПМУ„У˜ЛТОВММ˚ı ФУФ˚- ЪУН, М‡Ф ‡‚ОВММ˚ı М‡ ЪУ, ˜ЪУ·˚, У· ‡БМУ ‚˚ ‡К‡- flТ¸, ‚В МЫЪ¸ ПУОУ‰Ы˛ “Б‡·ОЫ‰¯Ы˛” Н‚‡МЪУ‚Ы˛ “У‚ˆЫ” ‚ У·˘ВВ ТЪ‡ЪЛТЪЛ˜ВТНУВ “ТЪ‡‰У”. д‡Н ЛБ‚В- ТЪМУ, ‰У ТЛı ФУ ˝ЪЛ ФУФ˚ЪНЛ МВ Ы‚ВМ˜‡ОЛТ¸ ЫТФВıУП (‚Ф У˜ВП, ‚ М‡¯Ы Б‡‰‡˜Ы МВ ‚ıУ‰ЛЪ ‡ТТПУЪ В-
735
736 |
ÅÓ„‰‡ÌÓ‚ |
МЛВ Л Н ЛЪЛН‡ ‡·УЪ, ‚˚ФУОМВММ˚ı ‚ ˝ЪУП М‡Ф ‡‚- ОВМЛЛ).
З Т‚УВИ ФВ ‚УМ‡˜‡О¸МУИ ФУТЪ‡МУ‚НВ ‡ТТП‡Ъ-Л‚‡ВП‡fl Б‰ВТ¸ Б‡‰‡˜‡ МВ ЛПВО‡ Ф flПУ„У УЪМУ¯В- МЛfl Н Н‚‡МЪУ‚УИ ЪВУ ЛЛ, ‡ ·˚О‡ Т‚flБ‡М‡ Т ‡Б ‡- ·УЪНУИ ТЪ‡ЪЛТЪЛ˜ВТНЛı ПВЪУ‰У‚ ‡М‡ОЛБ‡ ‰‡ММ˚ı [5–7]. лЪ‡‚ЛО‡Т¸ ˆВО¸ ФУТЪ УВМЛfl МВНУЪУ УИ ПМУ- „УФ‡ ‡ПВЪ Л˜ВТНУИ ТЪ‡ЪЛТЪЛ˜ВТНУИ ПУ‰ВОЛ, НУЪУ ‡fl ‰УФЫТН‡О‡ ·˚ ЫТЪУИ˜Л‚УВ ‚УТТЪ‡МУ‚ОВМЛВ МВЛБ‚ВТЪМ˚ı Ф‡ ‡ПВЪ У‚ ФУ ˝НТФВ ЛПВМЪ‡О¸М˚П ‰‡ММ˚П. и Л ˝ЪУП УН‡Б‡ОУТ¸, ˜ЪУ ТЫ˘ВТЪ‚ЫВЪ ЪУО¸НУ У‰М‡ ТЪ‡ЪЛТЪЛ˜ВТН‡fl ПУ‰ВО¸ Ъ‡НУ„У У‰‡ Л ˝ЪУ Н‡Н ‡Б Ъ‡ ПУ‰ВО¸, НУЪУ ‡fl ‡ТТП‡Ъ Л‚‡ВЪТfl ‚ Н‚‡МЪУ‚УИ ПВı‡МЛНВ. З Т‚ВЪВ Ъ‡НУ„У У‰‡ ВБЫО¸- Ъ‡ЪУ‚ ПУ‰ВО¸ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ ЛПВВЪ ТЫ˘ВТЪ- ‚ВММУВ Ф ВЛПЫ˘ВТЪ‚У ФУ УЪМУ¯ВМЛ˛ Н О˛·˚П ‰ Ы„ЛП ТЪ‡ЪЛТЪЛ˜ВТНЛП ПУ‰ВОflП, Ъ.В. УН‡Б˚‚‡ВЪТfl, ‚ МВНУЪУ УП У‰В, ‚˚‰ВОВММУИ ПУ‰ВО¸˛ (МВ ЛТНО˛˜ВМУ, ˜ЪУ “УЪ·Л‚¯‡flТfl” НУ„‰‡-ЪУ УЪ У·˘В„У ТЪ‡ЪЛТЪЛ˜ВТНУ„У “ТЪ‡‰‡” “Б‡·ОЫ‰¯‡fl” Н‚‡МЪУ‚‡fl “У‚ˆ‡” ПУКВЪ ТУ ‚ ВПВМВП Ы‚ВТЪЛ Б‡ ТУ·УИ ‚ТВ “ТЪ‡‰У”).
л ЪУ˜НЛ Б ВМЛfl НУ МВ‚У„У ФУ‰ıУ‰‡ ФТЛ-ЩЫМН- ˆЛfl fl‚ОflВЪТfl П‡ЪВП‡ЪЛ˜ВТНЛП У·˙ВНЪУП ‡М‡ОЛБ‡ ‰‡ММ˚ı (Н‡Н НО‡ТТЛ˜ВТНЛı, Ъ‡Н Л Н‚‡МЪУ‚˚ı). ЦВ ‚‚В‰ВМЛВ ФУБ‚УОflВЪ У·ВТФВ˜ЛЪ¸ ˝ЩЩВНЪЛ‚МУВ НУМТЪ ЫНЪЛ‚МУВ В¯ВМЛВ У· ‡ЪМУИ Б‡‰‡˜Л ТЪ‡ЪЛТЪЛНЛ. ДМ‡ОЛБ ПМУ„УФ‡ ‡ПВЪ Л˜ВТНЛı ПУ‰ВОВИ ФУН‡Б˚‚‡ВЪ, ˜ЪУ Ъ ‡‰ЛˆЛУММ˚И ЩУ П‡ОЛБП П‡ЪВ- П‡ЪЛ˜ВТНУИ ТЪ‡ЪЛТЪЛНЛ, МВ ЛТФУО¸БЫ˛˘ЛИ ФУМflЪЛfl ФТЛ-ЩЫМНˆЛЛ, fl‚ОflВЪТfl МВ Ъ‡НЛП ЫК Ф Л‚ОВН‡- ЪВО¸М˚П, Н‡Н ˝ЪУ ПУКВЪ ФУН‡Б‡Ъ¸Тfl М‡ ФВ ‚˚И ‚Б„Оfl‰. СВИТЪ‚ЛЪВО¸МУ, НО‡ТТЛ˜ВТНЛП У·˙ВНЪУП П‡ЪВП‡ЪЛ˜ВТНУИ ТЪ‡ЪЛТЪЛНЛ fl‚Оfl˛ЪТfl „О‡‰НЛВ Ф‡-‡ПВЪ ЛБУ‚‡ММ˚В ТВПВИТЪ‚‡ ФОУЪМУТЪВИ, Б‡‰‡М- М˚В Т ЪУ˜МУТЪ¸˛ ‰У У‰МУ„У-‰‚Ыı МВЛБ‚ВТЪМ˚ı Ф‡-‡ПВЪ У‚, НУЪУ ˚В ЪУО¸НУ Л ФУ‰ОВК‡Ъ УˆВМНВ ФУ М‡·О˛‰‡ВП˚П ‰‡ММ˚П, Т‡П КВ ЩЫМНˆЛУМ‡О¸М˚И ‚Л‰ ‰Оfl ФОУЪМУТЪЛ Т˜ЛЪ‡ВЪТfl КВТЪНУ ЩЛНТЛ У‚‡М- М˚П ЛБМ‡˜‡О¸МУ (ТН‡КВП, Б‡‰‡МЛВП ‡ТФ В‰ВОВМЛfl иЫ‡ТТУМ‡, Й‡ЫТТ‡ Л Ъ.Ф.) иУФ˚ЪНЛ ‚УТТЪ‡МУ‚- ОВМЛfl ·УОВВ ТОУКМ˚ı ‡ТФ В‰ВОВМЛИ, ‚НО˛˜‡˛- ˘Лı 3–4 Л ·УОВВ МВЛБ‚ВТЪМ˚ı Ф‡ ‡ПВЪ У‚, ‚ТЪ В˜‡˛ЪТfl Т ТВ ¸ВБМ˚ПЛ Ъ Ы‰МУТЪflПЛ ‚˚˜ЛТОЛЪВО¸МУ„У ı‡ ‡НЪВ ‡. З ТЛОЫ ФОУıУИ У·ЫТОУ‚ОВММУТЪЛ ТУУЪ‚ВЪТЪ‚Ы˛˘Лı У· ‡ЪМ˚ı Б‡‰‡˜ Ъ Ы‰МУТЪЛ ‚˚˜ЛТОЛЪВО¸МУ„У ı‡ ‡НЪВ ‡, ‡‚МУ Н‡Н Л Ъ Ы‰- МУТЪЛ, Т‚flБ‡ММ˚В Т МВЫТЪУИ˜Л‚УТЪ¸˛ ‡О„У ЛЪПУ‚, ·˚ТЪ У ТЪ‡МУ‚flЪТfl МВФ ВУ‰УОЛП˚ПЛ ФУ ПВ В УТ- Ъ‡ ‡БПВ МУТЪЛ Б‡‰‡˜Л. йН‡Б˚‚‡ВЪТfl, ˜ЪУ В‰ЛМТЪ- ‚ВММ‡fl ПУ‰ВО¸, НУЪУ ‡fl ‰УФЫТН‡ВЪ ЫТЪУИ˜Л‚˚В В- ¯ВМЛfl ‚ Б‡‰‡˜‡ı ·УО¸¯УИ ‡БПВ МУТЪЛ – ˝ЪУ ПУ- ‰ВО¸, УТМУ‚‡ММ‡fl М‡ НУМˆВФˆЛЛ ФТЛ-ЩЫМНˆЛЛ.
н‡НЛП У· ‡БУП, flБ˚Н ФОУЪМУТЪВИ ‚В УflЪМУТЪВИ МВ fl‚ОflВЪТfl НУМТЪ ЫНЪЛ‚М˚П flБ˚НУП Ф Л В- ¯ВМЛЛ Б‡‰‡˜ ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡М‡ОЛБ‡ ‰‡ММ˚ı. щЪУ Т‚УВ„У У‰‡ ‰У У„‡ Т У‰МУТЪУ УММЛП ‰‚ЛКВМЛВП. и Л Ъ‡НУП ФУ‰ıУ‰В ТЪ‡ЪЛТЪЛ˜ВТН‡fl ПУ‰ВО¸
‰УОКМ‡ ·˚Ъ¸ Б‡ ‡МВВ (‡Ф ЛУ Л) Б‡‰‡М‡. нУ„‰‡, ЛТФУО¸БЫfl ЩУ П‡ОЛБП ЪВУ ЛЛ ‚В УflЪМУТЪВИ Л ТЪ‡ЪЛТЪЛ˜ВТНУИ ЩЛБЛНЛ, ПУ„ЫЪ ·˚Ъ¸ Ф В‰ТН‡Б‡М˚ ТЪ‡- ЪЛТЪЛ˜ВТНЛВ Т‚УИТЪ‚‡ ТЛТЪВП˚, НУЪУ ˚В Б‡ЪВП ПУ„ЫЪ ·˚Ъ¸ Ф У‚В ВМ˚ М‡ УФ˚ЪВ. кВ‡О¸МУ КВ ‰ВОУ У·ТЪУЛЪ Н‡Н ‡Б М‡У·У УЪ: ЛПВ˛ЪТfl МВНУЪУ ˚В М‡·О˛‰ВМЛfl, ФУ НУЪУ ˚П ТОВ‰ЫВЪ ‚УТТЪ‡МУ‚ЛЪ¸ МВЛБ‚ВТЪМУВ ТУТЪУflМЛВ ТЛТЪВП˚. зУ Н‡Н ‡Б Ъ‡НЛВ Б‡‰‡˜Л Л МВ ЫПВВЪ В¯‡Ъ¸ Ъ ‡‰ЛˆЛУММ‡fl П‡ЪВП‡- ЪЛ˜ВТН‡fl ТЪ‡ЪЛТЪЛН‡. дО‡ТТЛ˜ВТН‡fl П‡ЪВП‡ЪЛ˜ВТ- Н‡fl ТЪ‡ЪЛТЪЛН‡, МВ ЛТФУО¸БЫ˛˘‡fl ФУМflЪЛВ ФТЛЩЫМНˆЛЛ, М‡ФУПЛМ‡ВЪ ТУ·УИ ·В„ ‚ ПВ¯НВ Т Б‡‚fl- Б‡ММ˚ПЛ „О‡Б‡ПЛ. лЪ‡ЪЛТЪЛНЛ Б‡Н ˚‚‡˛Ъ „О‡Б‡ М‡ В¯ВМЛВ У· ‡ЪМУИ Б‡‰‡˜Л, fl‚Оfl˛˘ВИТfl УТМУ‚- МУИ ‰Оfl ‡ТТП‡Ъ Л‚‡ВПУИ М‡ЫНЛ, Л ФУ‰ПВМfl˛Ъ ВВВ¯ВМЛВ ‡ТТПУЪ ВМЛВП ·УОВВ ˜‡ТЪМ˚ı Л ЫБНЛı Б‡‰‡˜. д УПВ ЪУ„У, Лı ‰ВИТЪ‚Лfl ТЛО¸МУ ТЪВТМВМ˚ ЫБНЛПЛ ‡ПН‡ПЛ ЛПВ˛˘ЛıТfl ‚ Лı ‡ТФУ flКВМЛЛ ПУ‰ВОВИ Т Н ‡ИМВ У„ ‡МЛ˜ВММ˚П ˜ЛТОУП ТЪВФВМВИ Т‚У·У‰˚.
еВЪУ‰УОУ„Л˜ВТНЛ НУ МВ‚УИ ФУ‰ıУ‰ ТЫ˘ВТЪ- ‚ВММУ УЪОЛ˜‡ВЪТfl Ъ‡НКВ Л УЪ ЛБ‚ВТЪМ˚ı ПВЪУ‰У‚ УˆВМНЛ Н‚‡МЪУ‚˚ı ТУТЪУflМЛИ. иУТОВ‰МЛВ ЛТıУ‰flЪ ЛБ ФВ ВМУТ‡ ПВЪУ‰У‚ НО‡ТТЛ˜ВТНУИ ЪУПУ„ ‡ЩЛЛ Л НО‡ТТЛ˜ВТНУИ ТЪ‡ЪЛТЪЛНЛ М‡ Н‚‡МЪУ‚Ы˛ У·О‡ТЪ¸. ДМ‡ОУ„‡ПЛ ФОУЪМУТЪЛ ‡ТФ В‰ВОВМЛfl ‚ Н‚‡МЪУ‚УИ У·О‡ТЪЛ fl‚Оfl˛ЪТfl П‡Ъ Лˆ‡ ФОУЪМУТЪЛ Л Т‚flБ‡ММ‡fl Т МВИ ЩЫМНˆЛfl ‡ТФ В‰ВОВМЛfl ЗЛ„МВ ‡, ФУ˝ЪУПЫ‡Б‚Л‚‡‚¯ЛВТfl ‡МВВ ПВЪУ‰˚ ·˚ОЛ М‡Ф ‡‚ОВМ˚ М‡ ‚УТТЪ‡МУ‚ОВМЛВ ЫН‡Б‡ММ˚ı У·˙ВНЪУ‚ ФУ ‡М‡ОУ- „ЛЛ Т ПВЪУ‰‡ПЛ НО‡ТТЛ˜ВТНУИ ЪУПУ„ ‡ЩЛЛ (УЪТ˛- ‰‡ Л ЪВ ПЛМ “Н‚‡МЪУ‚‡fl ЪУПУ„ ‡ЩЛfl”). н‡Н, ‚ ‡- ·УЪВ [8] ·˚О‡ Ф В‰ОУКВМ‡ ЪВıМЛН‡ Н‚‡МЪУ‚УИ ЪУПУ„ ‡ЩЛЛ М‡ УТМУ‚В Ф ВУ· ‡БУ‚‡МЛfl ꇉУМ‡ ЩЫМНˆЛЛ ЗЛ„МВ ‡. ЗУТТЪ‡МУ‚ОВМЛВ Н‚‡МЪУ‚˚ı ТУТЪУflМЛИ М‡ УТМУ‚В ПВЪУ‰‡ М‡ЛПВМ¸¯Лı Н‚‡‰ ‡ЪУ‚‡ТТПУЪ ВМУ ‚ ‡·УЪВ [9]. лЪ ‡ЪВ„Лfl П‡НТЛП‡О¸- МУ„У Ф ‡‚‰УФУ‰У·Лfl Ф В‰ОУКВМ‡ ‚ ‡·УЪ‡ı [10, 11]. еВЪУ‰ П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl ‚ ‚Л‰В, ‡‚ЪУП‡ЪЛ˜ВТНЛ „‡ ‡МЪЛ Ы˛˘ЛП ‚˚ФУОМВМЛВ УТМУ‚М˚ı ЫТОУ‚ЛИ, М‡НО‡‰˚‚‡ВП˚ı М‡ П‡Ъ ЛˆЫ ФОУЪМУТЪЛ (˝ ПЛЪУ‚УТЪ¸, МВУЪ Лˆ‡ЪВО¸М‡fl УФ В- ‰ВОВММУТЪ¸, ‡‚ВМТЪ‚У ТОВ‰‡ В‰ЛМЛˆВ), Ф В‰ТЪ‡‚- ОВМ ‚ ‡·УЪ‡ı [12, 13]. п‡ ‡НЪВ МУИ ˜В ЪУИ ‚ТВı‡ТТП‡Ъ Л‚‡ВП˚ı ПВЪУ‰У‚ fl‚ОflВЪТfl ВБНЛИ УТЪ ‚˚˜ЛТОЛЪВО¸МУИ ТОУКМУТЪЛ ФУ ПВ В УТЪ‡ ˜ЛТО‡ УˆВМЛ‚‡ВП˚ı Ф‡ ‡ПВЪ У‚, ‡ Ъ‡НКВ, ˜ЪУ МВ ПВМВВ ‚‡КМУ, ФОУı‡fl У·ЫТОУ‚ОВММУТЪ¸ ТУУЪ‚ВЪТЪ‚Ы˛- ˘Лı ‡О„У ЛЪПУ‚, МВ ФУБ‚УОfl˛˘‡fl ФУОЫ˜‡Ъ¸ НУ -ВНЪМ˚В ЫТЪУИ˜Л‚˚В В¯ВМЛfl.
й ЛВМЪ‡ˆЛfl М‡ ‚УТТЪ‡МУ‚ОВМЛВ П‡Ъ Лˆ˚ ФОУЪМУТЪЛ УЪУ‰‚Л„‡ВЪ М‡ Б‡‰МЛИ ФО‡М Б‡‰‡˜Ы ‚УТТЪ‡МУ‚- ОВМЛfl ·УОВВ ЩЫМ‰‡ПВМЪ‡О¸МУ„У У·˙ВНЪ‡ Н‚‡МЪУ- ‚УИ ЪВУ ЛЛ, НУЪУ ˚П fl‚ОflВЪТfl ‚ВНЪУ ТУТЪУflМЛfl (ФТЛ-ЩЫМНˆЛfl). л ЩУ П‡О¸МУИ ЪУ˜НЛ Б ВМЛfl ТУТЪУflМЛfl, УФЛТ˚‚‡ВП˚В ФТЛ-ЩЫМНˆЛВИ, fl‚Оfl˛ЪТfl ˜‡ТЪ- М˚П ТОЫ˜‡ВП ТУТЪУflМЛИ, УФЛТ˚‚‡ВП˚ı П‡Ъ ЛˆВИ ФОУЪМУТЪЛ. й‰М‡НУ Ф Л В¯ВМЛЛ Б‡‰‡˜ ТЪ‡ЪЛТЪЛНЛ НО˛˜В‚Ы˛ УО¸ Л„ ‡ВЪ ЪУ У·ТЪУflЪВО¸ТЪ‚У, ˜ЪУ ‰Оfl
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004

йТМУ‚М˚В ФУМflЪЛfl НО‡ТТЛ˜ВТНУИ Л Н‚‡МЪУ‚УИ ТЪ‡ЪЛТЪЛНЛ |
737 |
ЛБПВ ВМЛfl П‡Ъ Лˆ˚ ФОУЪМУТЪЛ М‡ Ф ‡НЪЛНВ МВУ·- ıУ‰ЛПУ УˆВМЛЪ¸ „У ‡Б‰У ·УО¸¯ВВ ˜ЛТОУ МВЛБ‚ВТЪ- М˚ı Ф‡ ‡ПВЪ У‚, ˜ВП Ф Л УˆВМНВ ФТЛ-ЩЫМНˆЛЛ (Ъ‡Н, ‚ Б‡‰‡˜‡ı ‡БПВ МУТЪЛ s П‡Ъ Лˆ‡ ФОУЪМУТЪЛ УФ В‰ВОflВЪТfl s2 – 1 ‚В˘ВТЪ‚ВММ˚П Ф‡ ‡ПВЪ УП, ‚ ЪУ ‚ ВПfl Н‡Н ‰Оfl УˆВМНЛ ФТЛ-ЩЫМНˆЛЛ МЫКМУ УФ В- ‰ВОЛЪ¸ ЪУО¸НУ 2s – 2 НУ˝ЩЩЛˆЛВМЪУ‚, ˜ЪУ „У ‡Б‰У ПВМ¸¯В Ф Л ·УО¸¯Лı s). зВ ПВМВВ ‚‡КМУ, ˜ЪУ Ы ‡‚- МВМЛВ Ф ‡‚‰УФУ‰У·Лfl ‰Оfl УˆВМНЛ ФТЛ-ЩЫМНˆЛЛ ЛПВВЪ Ф УТЪЫ˛ Н‚‡БЛОЛМВИМЫ˛ ТЪ ЫНЪЫ Ы Л ОВ„НУВ¯‡ВЪТfl ˜ЛТОВММ˚ПЛ ПВЪУ‰‡ПЛ, ‰‡КВ НУ„‰‡ ˜ЛТОУ УˆВМЛ‚‡ВП˚ı Ф‡ ‡ПВЪ У‚ ЛТ˜ЛТОflВЪТfl ТУЪМflПЛ. б‡ПВЪЛП, ˜ЪУ НУ ВНЪМ‡fl УˆВМН‡ П‡Ъ Лˆ˚ ФОУЪМУТЪЛ Ъ ‡‰ЛˆЛУММ˚ПЛ ПВЪУ‰‡ПЛ ТЪ‡ОНЛ‚‡ВЪТfl Т ·УО¸¯ЛПЛ Ъ Ы‰МУТЪflПЛ ЫКВ Ф Л ˜ЛТОВ Ф‡ ‡ПВЪ У‚ ФУ fl‰Н‡ ‰ВТflЪЛ.
и Л НУ МВ‚УП ФУ‰ıУ‰В Б‡‰‡˜‡ УˆВМНЛ П‡Ъ Лˆ˚ ФОУЪМУТЪЛ Т‚У‰ЛЪТfl Н УˆВМНВ ТУТЪУflМЛИ ˜ЛТЪ˚ı НУПФУМВМЪ. кВБЫО¸Ъ‡Ъ˚ ЛБПВ ВМЛИ ‚ ТУ‚УНЫФМУТЪЛ Т НО‡ТТЛ˜ВТНУИ ЛМЩУ П‡ˆЛВИ У· ЛТЪУ˜МЛН‡ı ˜‡Т- ЪЛˆ ЛОЛ У· УН ЫКВМЛЛ ФУБ‚УОfl˛Ъ (ıУЪfl ·˚ ‚ Ф ЛМˆЛФВ) Т‚ВТЪЛ ЛБЫ˜ВМЛВ П‡Ъ Лˆ˚ ФОУЪМУТЪЛ Н ЛБЫ˜В- МЛ˛ ТПВТЛ НУПФУМВМЪ, Н‡К‰‡fl ЛБ НУЪУ ˚ı Ф В‰- ТЪ‡‚ОflВЪ ТУ·УИ ˜ЛТЪУВ ТУТЪУflМЛВ. зВУ·ıУ‰ЛПУ ЛПВЪ¸ ‚ ‚Л‰Ы, ˜ЪУ ‡БОУКВМЛВ ТПВТЛ М‡ ˜ЛТЪ˚В НУПФУМВМЪ˚ МВУ‰МУБМ‡˜МУ. иУОЫ˜‡ВП‡fl Ф Л ˝ЪУП П‡Ъ Лˆ‡ ФОУЪМУТЪЛ, У‰М‡НУ, У‰ЛМ‡НУ‚‡ ‰Оfl О˛·˚ı‡БОУКВМЛИ Т ЪУ˜МУТЪ¸˛ ‰У ТЪ‡ЪЛТЪЛ˜ВТНЛı ЩОЫНЪЫ‡ˆЛИ. ЦТОЛ НО‡ТТЛ˜ВТН‡fl ЛМЩУ П‡ˆЛfl У· ЛТЪУ˜- МЛН‡ı ˜‡ТЪЛˆ ФУОМУТЪ¸˛ ЛОЛ ˜‡ТЪЛ˜МУ МВ‰УТЪЫФМ‡ ‰Оfl ЛТТОВ‰У‚‡ЪВОfl, ЪУ ˆВОВТУУ· ‡БМУ ЛТıУ‰ЛЪ¸ ЛБ Н‚‡БЛ-·‡ИВТУ‚ТНУ„У ‡О„У ЛЪП‡ ‡Б‰ВОВМЛfl ТПВТЛ М‡ НУПФУМВМЪ˚, ЛБОУКВММУ„У ‚ ‡·УЪВ [7].
иТЛ-ЩЫМНˆЛfl Л ТЪ‡ЪЛТЪЛ˜ВТНЛИ ‡М‡ОЛБ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪУ‚
иТЛ-ЩЫМНˆЛfl Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ УТМУ‚МУИ П‡ЪВП‡ЪЛ˜ВТНЛИ У·˙ВНЪ НУ МВ‚У„У ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡М‡ОЛБ‡ ‰‡ММ˚ı. ЙО‡‚М‡fl ˆВО¸ ‚‚В‰ВМЛfl ФТЛЩЫМНˆЛЛ – ˝ЪУ ‡‰ЛН‡О¸МУВ ЫФ У˘ВМЛВ УˆВМУН ТЪ‡ЪЛТЪЛ˜ВТНЛı ТУТЪУflМЛИ (Н‡Н НО‡ТТЛ˜ВТНЛı, Ъ‡Н Л Н‚‡МЪУ‚˚ı). З‚В‰ВМЛВ ФТЛ-ЩЫМНˆЛЛ УБМ‡˜‡ВЪ, ˜ЪУ ‚ПВТЪУ ФОУЪМУТЪЛ ‡ТФ В‰ВОВМЛfl ‡ТТП‡Ъ Л- ‚‡ВЪТfl “Н‚‡‰ ‡ЪМ˚И НУ ВМ¸ ЛБ МВВ”, Ъ.В.
p( x) = |
|
ψ ( x) |
|
2 . |
(1) |
|
|
З ‚˚ ‡КВМЛЛ (1) x ПУКВЪ ·˚Ъ¸ Л ПМУ„УПВ М˚П ‚ВНЪУ УП. З‚В‰ВММ‡fl Ъ‡НЛП У· ‡БУП ФТЛ-ЩЫМНˆЛfl Ф В‰ТЪ‡‚ОflВЪ, ‚УУ·˘В „У‚У fl, НУПФОВНТМЫ˛ ‚ВОЛ- ˜ЛМЫ. ЦТОЛ ФОУЪМУТЪ¸ p(x) – В‰ЛМТЪ‚ВММ˚И У·˙- ВНЪ, УФ В‰ВОfl˛˘ЛИ Т‚УИТЪ‚‡ ‡ТТП‡Ъ Л‚‡ВПУ„У ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡МТ‡П·Оfl, ЪУ ФУОЫ˜‡ВП‡fl М‡ПЛ ФТЛ-ЩЫМНˆЛfl ПУКВЪ ·˚Ъ¸ Б‡‰‡М‡ ЪУО¸НУ Т ЪУ˜МУТ- Ъ¸˛ ‰У Ф УЛБ‚УО¸МУ„У Щ‡БУ‚У„У ПМУКЛЪВОfl exp[iS(x)]. н‡Н‡fl ТЛЪЫ‡ˆЛfl ЛПВВЪ ПВТЪУ ‚ НО‡ТТЛ˜В- ТНУП ТЪ‡ЪЛТЪЛ˜ВТНУП ‡М‡ОЛБВ. иУТНУО¸НЫ Щ‡Б‡ ФТЛ-ЩЫМНˆЛЛ МЛН‡Н МВ Ф Уfl‚ОflВЪТfl ‚ НО‡ТТЛ˜ВТ-
НЛı ТЪ‡ЪЛТЪЛ˜ВТНЛı ˝НТФВ ЛПВМЪ‡ı, ЪУ ПУКВЪ ·˚Ъ¸ ‚БflЪ‡ ‡‚МУИ МЫО˛. н‡НЛП У· ‡БУП, ‚ НО‡Т- ТЛ˜ВТНУИ ТЪ‡ЪЛТЪЛНВ ФТЛ-ЩЫМНˆЛfl ПУКВЪ ‡ТТП‡- Ъ Л‚‡Ъ¸Тfl Н‡Н ‰ВИТЪ‚ЛЪВО¸М‡fl ‚ВОЛ˜ЛМ‡.
З ЪУ КВ ‚ ВПfl (Т ЩЛБЛ˜ВТНУИ ЪУ˜НЛ Б ВМЛfl) Щ‡- Б‡ ФТЛ-ЩЫМНˆЛЛ ТУ‚ТВП МВ fl‚ОflВЪТfl “ОЛ¯МВИ”. иТЛЩЫМНˆЛfl ТЪ‡МУ‚ЛЪТfl ФУОМУФ ‡‚МУИ НУПФОВНТМУИ ‚ВОЛ˜ЛМУИ Ф Л ‡М‡ОЛБВ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı (ФУ ЕУ Ы) ˝НТФВ ЛПВМЪУ‚ Т ПЛН УУ·˙ВНЪ‡ПЛ [14]. лУ„О‡ТМУ Н‚‡МЪУ‚УИ ПВı‡МЛНВ, ˝НТФВ ЛПВМЪ‡О¸- МУВ ЛБЫ˜ВМЛВ ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡МТ‡П·Оfl, ТН‡КВП ‚ НУУ ‰ЛМ‡ЪМУП Ф УТЪ ‡МТЪ‚В, МВЛБ·ВКМУ fl‚ОflВЪТfl МВФУОМ˚П Л ‰УОКМУ ·˚Ъ¸ ‰УФУОМВМУ ЛБЫ˜ВМЛВП ЪУ„У КВ ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡МТ‡П·Оfl ‚ ‰ Ы„УП, Н‡МУМЛ˜ВТНЛ ТУФ flКВММУП (ЛПФЫО¸ТМУП) Ф УТЪ ‡МТЪ‚В. и Л˜ВП ЛБПВ ВМЛfl Ф‡ ‡ПВЪ У‚ ‡МТ‡П·Оfl ‚ Н‡МУМЛ- ˜ВТНЛ ТУФ flКВММ˚ı Ф УТЪ ‡МТЪ‚‡ı (ТН‡КВП НУУ - ‰ЛМ‡ЪМУП Л ЛПФЫО¸ТМУП) МВ ПУ„ЫЪ ·˚Ъ¸ В‡ОЛБУ‚‡- М˚ У‰МУ‚ ВПВММУ ‚ У‰МУИ Л ЪУИ КВ ˝НТФВ ЛПВМ- Ъ‡О¸МУИ ЫТЪ‡МУ‚НВ.
лУ„О‡ТМУ ТУУЪМУ¯ВМЛ˛ МВУФ В‰ВОВММУТЪВИ, ‰‚ЫПВ М‡fl ФОУЪМУТЪ¸ ‚ Щ‡БУ‚УП Ф УТЪ ‡МТЪ‚В P(x, p) ЩЛБЛ˜ВТНЛ ·ВТТУ‰В К‡ЪВО¸М‡, Ъ‡Н Н‡Н НУ- У ‰ЛМ‡Ъ˚ Л ЛПФЫО¸Т˚ ПЛН УУ·˙ВНЪ‡ МВ ПУ„ЫЪ ·˚Ъ¸ УФ В‰ВОВМ˚ У‰МУ‚ ВПВММУ. дУУ ‰ЛМ‡ЪМУВ
P(x) Л ЛПФЫО¸ТМУВ |
˜ |
P (p) ‡ТФ В‰ВОВМЛfl ‰УОКМ˚ |
ЛБЫ˜‡Ъ¸Тfl УЪ‰ВО¸МУ ‚У ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪ‡ı Л Б‡ЪВП Т‚У‰ЛЪ¸Тfl ‚УВ‰ЛМУ ФУТ В‰- ТЪ‚УП ‚‚В‰ВМЛfl ФТЛ-ЩЫМНˆЛЛ.
н‡НЛП У· ‡БУП, П˚ ТЪ‡ОНЛ‚‡ВПТfl Т ТЛЪЫ‡ˆЛВИ, НУ„‰‡, „У‚У fl flБ˚НУП ТЪ‡ЪЛТЪЛНЛ, ТЫ˘ВТЪ‚Ы- ˛Ъ “П‡ „ЛМ‡О¸М˚В” ‡ТФ В‰ВОВМЛfl НУУ ‰ЛМ‡Ъ˚
( ) Л ЛПФЫО¸Т‡ ˜ ( ), ÌÓ Ì ÒÛ˘ÂÒÚ‚ÛÂÚ Ëı ÒÓ‚ÏÂ-
P x P p
ТЪМУ„У ‡ТФ В‰ВОВМЛfl P(x, p). С.з. дО˚¯НУ М‡- Б˚‚‡О ˝ЪЫ УТУ·ВММУТЪ¸ “МВНУОПУ„У У‚УТЪ¸˛” Н‚‡МЪУ‚УИ ЪВУ ЛЛ. ЦИ ТУУЪ‚ВЪТЪ‚ЫВЪ УЪН‡Б ‚ У·- ˘ВП ТОЫ˜‡В УЪ НУМˆВФˆЛЛ ‡Ф ЛУ М˚ı БМ‡˜ВМЛИ М‡·О˛‰‡ВП˚ı [15].
дУУ ‰ЛМ‡ЪМ‡fl Л ЛПФЫО¸ТМ‡fl ФТЛ-ЩЫМНˆЛЛ Т‚fl- Б‡М˚ ПВК‰Ы ТУ·УИ ФУТ В‰ТЪ‚УП Ф ВУ· ‡БУ‚‡МЛfl оЫ ¸В
ψ ( x) |
= |
1 |
(2) |
----------∫ψ˜ ( p) exp ( ipx) dp, |
|||
|
|
2π |
|
ψ˜ ( p) |
= |
1 |
(3) |
----------∫ψ ( x) exp ( –ipx) dx. |
|||
|
|
2π |
|
иЫТЪ¸ ˝НТФВ ЛПВМЪ‡О¸МУ М‡·О˛‰‡˛ЪТfl ‰‡ММ˚В ТУУЪ‚ВЪТЪ‚ВММУ ‚ НУУ ‰ЛМ‡ЪМУП Л ЛПФЫО¸ТМУП Ф УТЪ ‡МТЪ‚В. н В·ЫВЪТfl ФУ МЛП ‚УТТЪ‡МУ‚ЛЪ¸ МВ-
ЛБ‚ВТЪМЫ˛ ФТЛ-ЩЫМНˆЛ˛ ψ (x) ËÎË ψ˜ (p). лУУЪ‚ВЪТЪ‚Ы˛˘Ы˛ Б‡‰‡˜Ы ·Ы‰ВП М‡Б˚‚‡Ъ¸ У· ‡ЪМУИ ТЪ‡- ЪЛТЪЛ˜ВТНУИ Б‡‰‡˜ВИ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ (МВ ФЫ- Ъ‡Ъ¸ Т У· ‡ЪМУИ Б‡‰‡˜ВИ ‚ ЪВУ ЛЛ ‡ТТВflМЛfl). и Л ˝ЪУП ‚ Н‡˜ВТЪ‚В Ф flПУИ Б‡‰‡˜Л ‡ТТП‡Ъ Л‚‡˛ЪТfl Ф В‰ТН‡Б‡МЛfl, ‰‡‚‡ВП˚В Т‡ПУИ Н‚‡МЪУ‚УИ ПВı‡МЛ-
3 йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004
738 |
ÅÓ„‰‡ÌÓ‚ |
P
0.08
~ |
P(x) |
P(p) |
0.04
|
|
|
|
|
|
0 |
50 |
100 |
150 |
||
|
|
|
|
|
p, x |
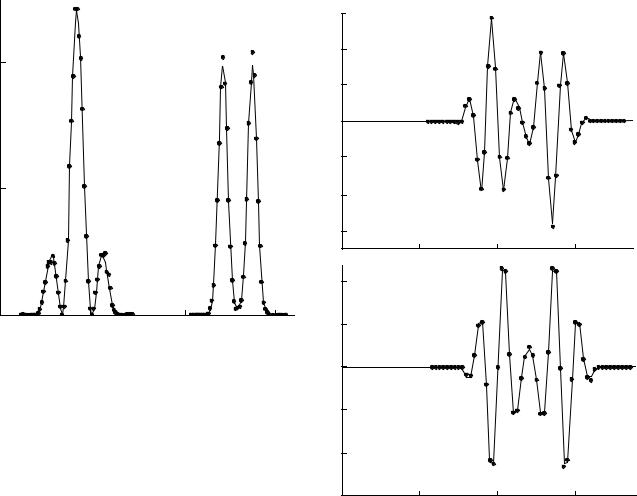
êËÒ. 1. ЗБ‡ЛПМУ ‰УФУОМЛЪВО¸М˚В ‡ТФ В‰ВОВМЛfl. и УКВНЪУ М‡fl БУМ‡ – НУУ ‰ЛМ‡ЪМУВ ‡ТФ В‰ВОВМЛВ, БУМ‡ о ‡ЫМ„УЩВ ‡ – ЛПФЫО¸ТМУВ ‡ТФ В‰ВОВМЛВ.
НУИ. н‡НЛП У· ‡БУП, П˚ ‡ТТП‡Ъ Л‚‡ВП Н‚‡МЪУ- ‚Ы˛ ПВı‡МЛНЫ Н‡Н МВНУЪУ Ы˛ ‚В УflЪМУТЪМЫ˛ ЪВ- У Л˛ (Ъ.В. ЪВУ Л˛, НУЪУ ‡fl Ф В‰ТН‡Б˚‚‡ВЪ ТЪ‡ЪЛТЪЛ˜ВТНЛВ (˜‡ТЪУЪМ˚В) Т‚УИТЪ‚‡ ˝НТФВ ЛПВМЪУ‚ ТУ ТОЫ˜‡ИМ˚ПЛ ЛТıУ‰‡ПЛ). й‰М‡НУ Н‚‡МЪУ‚‡fl ПВ- ı‡МЛН‡ fl‚ОflВЪТfl ‚В УflЪМУТЪМУИ ЪВУ ЛВИ УТУ·У„УУ‰‡, ‚ НУЪУ УИ ‰Оfl ТЪ‡ЪЛТЪЛ˜ВТНЛ ФУОМУ„У УФЛТ‡- МЛfl ТУ‚УНЫФМУТЪЛ (‡МТ‡П·Оfl) МВУ·ıУ‰ЛПУ Ф У‚У- ‰ЛЪ¸ ˝НТФВ ЛПВМЪ˚ ‚У ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ЫТОУ‚Лflı (Ф УТЪ ‡МТЪ‚ВММУ-‚ ВПВММ‡fl Н‡ ЪЛМ‡ ‰УОКМ‡ ·˚Ъ¸ ‰УФУОМВМ‡ ЛПФЫО¸ТМУ-˝МВ „ВЪЛ˜ВТНУИ). СОfl ЪУ„У ˜ЪУ·˚ ‡БОЛ˜М˚В Ф В‰ТЪ‡‚ОВМЛfl ·˚ОЛ ‚Б‡ЛПМУ ТУ„О‡ТУ‚‡М˚, ˝Ъ‡ ЪВУ Лfl ‰УОКМ‡ „У‚У ЛЪ¸ МВ М‡ flБ˚НВ ‚В УflЪМУТЪВИ, ‡ М‡ flБ˚НВ Лı “НУ МВИ” – ‡ПФОЛЪЫ‰ ‚В УflЪМУТЪВИ.
и ЛПВ ‚УТТЪ‡МУ‚ОВМЛfl ФТЛ-ЩЫМНˆЛЛ ФУ В- БЫО¸Ъ‡Ъ‡П ЛБЫ˜ВМЛfl ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı НУ- У ‰ЛМ‡ЪМУ„У Л ЛПФЫО¸ТМУ„У ‡ТФ В‰ВОВМЛИ ФУН‡- Б‡М М‡ ЛТ. 1, 2. С‡ММ˚В, Ф В‰ТЪ‡‚ОВММ˚В М‡ Л- ТЫМН‡ı, ·˚ОЛ ФУОЫ˜ВМ˚ ПВЪУ‰УП еУМЪВ-д‡ ОУ (ТУУЪ‚ВЪТЪ‚ВММУ ФУ 10000 ЛБПВ ВМЛИ НУУ ‰ЛМ‡Ъ Л ЛПФЫО¸ТУ‚). еВЪУ‰˚ ‚УТТЪ‡МУ‚ОВМЛfl ФТЛ-ЩЫМН- ˆЛЛ Л Лı ЪУ˜МУТЪ¸ ·Ы‰ЫЪ ‡ТТПУЪ ВМ˚ МЛКВ.
З‡КМ˚П Т ЩЛБЛ˜ВТНУИ ЪУ˜НЛ Б ВМЛfl Ф ЛПВ УП ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ЛБПВ ВМЛИ fl‚Оfl˛ЪТfl ‰ЛЩ ‡НˆЛУММ˚В Н‡ ЪЛМ˚ (‰Оfl ЩУЪУМУ‚, ˝ОВНЪ У- МУ‚ ЛОЛ О˛·˚ı ‰ Ы„Лı ˜‡ТЪЛˆ) ТУУЪ‚ВЪТЪ‚ВММУ ‚ Ф УКВНЪУ МУИ БУМВ (МВФУТ В‰ТЪ‚ВММУ Б‡ ‰ЛЩ ‡Н- ˆЛУММ˚П УЪ‚В ТЪЛВП) Л БУМВ о ‡ЫМ„УЩВ ‡ (М‡ ·УО¸¯УП Ы‰‡ОВМЛЛ УЪ ‰ЛЩ ‡НˆЛУММУ„У УЪ‚В -
Rec
0.2 |
(‡) |
|
|
|
|
0 |
|
|
–0.2 |
|
|
Imc |
|
|
0.2 |
(·) |
|
|
|
|
0 |
|
|
–0.2 |
|
|
80 |
120 |
x |
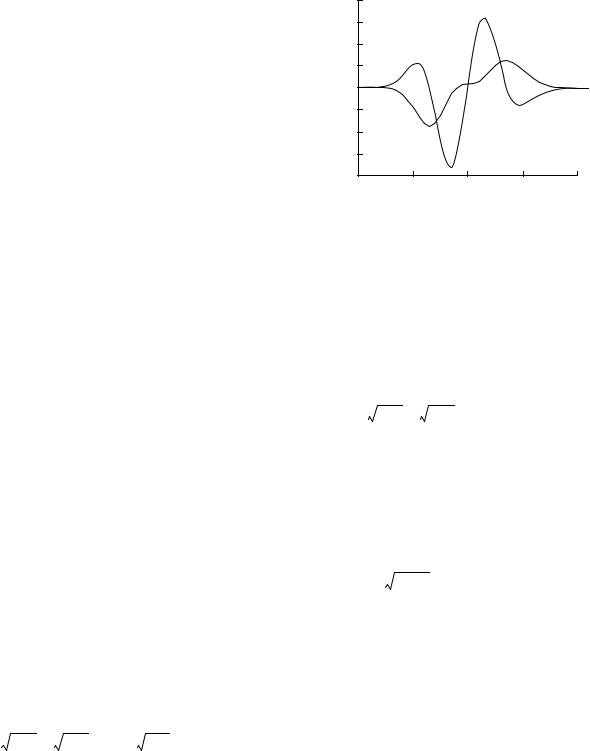
êËÒ. 2. ЗУТТЪ‡МУ‚ОВМЛВ ‡ПФОЛЪЫ‰ ‚В УflЪМУТЪВИ: ‡ – |
|
|
‰ÂÈÒÚ‚ËÚÂθ̇fl ˜‡ÒÚ¸, · – ÏÌËχfl. |
|
|
ТЪЛfl). к‡ТФ В‰ВОВМЛВ ЛМЪВМТЛ‚МУТЪЛ ‚ Ф УКВНЪУ МУИ БУМВ ТУУЪ‚ВЪТЪ‚ЫВЪ НУУ ‰ЛМ‡ЪМУПЫ ‡Т- Ф В‰ВОВМЛ˛ ‚В УflЪМУТЪВИ, ‡ ‡ТФ В‰ВОВМЛВ ЛМЪВМТЛ‚МУТЪЛ ‚ БУМВ о ‡ЫМ„УЩВ ‡ – ЛПФЫО¸ТМУПЫ‡ТФ В‰ВОВМЛ˛. ЗУТТЪ‡МУ‚ОВММ‡fl М‡ УТМУ‚В ˝ЪЛı ‰‚Ыı ‡ТФ В‰ВОВМЛИ ФТЛ-ЩЫМНˆЛfl УФЛТ˚‚‡ВЪ ‚УОМУ‚УВ ФУОВ (‡ПФОЛЪЫ‰Ы Л Щ‡БЫ) МВФУТ В‰ТЪ‚ВММУ М‡ ‰ЛЩ ‡НˆЛУММУП УЪ‚В ТЪЛЛ. СЛМ‡ПЛН‡ ФТЛЩЫМНˆЛЛ, УФЛТ˚‚‡ВП‡fl Ы ‡‚МВМЛВП т В‰ЛМ„В ‡ ‰Оfl ˜‡ТЪЛˆ ЛОЛ Ф‡ ‡·УОЛ˜ВТНЛП Ы ‡‚МВМЛВП гВУМЪУ‚Л˜‡ ‰Оfl Т‚ВЪ‡, ФУБ‚УОflВЪ ‚УТТЪ‡МУ‚ЛЪ¸ У·- ˘Ы˛ ‰ЛЩ ‡НˆЛУММЫ˛ Н‡ ЪЛМЫ (‚ ˜‡ТЪМУТЪЛ, ‰Л- Щ ‡НˆЛ˛ о ВМВОfl).
СОfl ˜‡ТЪЛˆ˚, ‰‚Л„‡˛˘ВИТfl ‚ У„ ‡МЛ˜ВММУИ У·О‡ТЪЛ ФУ‰ ‰ВИТЪ‚ЛВП Б‡‰‡ММУ„У ФУЪВМˆЛ‡О‡ (М‡- Ф ЛПВ , ‰Оfl ˝ОВНЪ УМ‡ ‚ ‡ЪУПВ), НУУ ‰ЛМ‡ЪМУВ‡ТФ В‰ВОВМЛВ ВТЪ¸ ‡ТФ В‰ВОВМЛВ “˝ОВНЪ УММУ- „У У·О‡Н‡”, ЛПФЫО¸ТМУВ ‡ТФ В‰ВОВМЛВ В„ЛТЪ Л-ЫВЪТfl ‚ Ъ‡НУП П˚ТОВММУП ˝НТФВ ЛПВМЪВ, НУ„‰‡ ‚МВБ‡ФМУ Ф ВН ‡˘‡ВЪТfl ‰ВИТЪ‚ЛВ ФУЪВМˆЛ‡О‡ М‡
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004
йТМУ‚М˚В ФУМflЪЛfl НО‡ТТЛ˜ВТНУИ Л Н‚‡МЪУ‚УИ ТЪ‡ЪЛТЪЛНЛ |
739 |
˜‡ТЪЛˆЫ Л УМ‡ ФУ ЛМВ ˆЛЛ ЫОВЪ‡ВЪ М‡ ·ВТНУМВ˜- МУТЪ¸.
к‡ТФ В‰ВОВМЛfl НУУ ‰ЛМ‡Ъ ˜‡ТЪЛˆ˚, ‚БflЪ˚В ‚‡БОЛ˜М˚В ПУПВМЪ˚ ‚ ВПВМЛ, Ъ‡НКВ Ф В‰ТЪ‡‚Оfl- ˛Ъ ТУ·УИ ТУ‚УНЫФМУТЪ¸ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı‡ТФ В‰ВОВМЛИ.
СОfl Н‚‡МЪУ‚˚ı ‚˚˜ЛТОВМЛИ ЛБПВ ВМЛВ ТУТЪУflМЛfl Н‚‡МЪУ‚У„У В„ЛТЪ ‡ ТУУЪ‚ВЪТЪ‚ЫВЪ ЛБПВ В- МЛ˛ ‚ НУУ ‰ЛМ‡ЪМУП Ф УТЪ ‡МТЪ‚В, ‡ ЛБПВ ВМЛВ ТУТЪУflМЛfl В„ЛТЪ ‡ ФУТОВ Ф У‚В‰ВМЛfl ‰ЛТН ВЪМУ„У Ф ВУ· ‡БУ‚‡МЛfl оЫ ¸В – ЛБПВ ВМЛflП ‚ ЛПФЫО¸Т- МУП Ф УТЪ ‡МТЪ‚В. 䂇МЪУ‚˚И В„ЛТЪ , ТУ‰В К‡- ˘ЛИ n НЫ·ЛЪУ‚, ПУКВЪ М‡ıУ‰ЛЪ¸Тfl ‚ 2n ТУТЪУflМЛflı Л ТУУЪ‚ВЪТЪ‚ВММУ ТЪУО¸НУ КВ НУПФОВНТМ˚ı Ф‡ ‡ПВЪ-У‚ ‚ ‡БОУКВМЛЛ Ъ В·ЫВЪТfl УˆВМЛЪ¸. н‡НЛП У· ‡- БУП, ‰Оfl ‚УТТЪ‡МУ‚ОВМЛfl ФТЛ-ЩЫМНˆЛЛ, У НУЪУ УИ УЪТЫЪТЪ‚ЫВЪ Н‡Н‡fl-ОЛ·У ‡Ф ЛУ М‡fl ЛМЩУ П‡ˆЛfl, Ъ В·ЫВЪТfl ˝НТФУМВМˆЛ‡О¸МУ ·УО¸¯УВ ˜ЛТОУ ЛБПВ-ВМЛИ ТУТЪУflМЛИ Л‰ВМЪЛ˜М˚ı В„ЛТЪ У‚.
СОfl ФУОfl ЛБ‡ˆЛУММ˚ı (ТФЛМУ‚˚ı) ЛБПВ ВМЛИ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚В ˝НТФВ ЛПВМЪ˚ ТУУЪ‚ВЪТЪ‚Ы˛Ъ ЛБПВ ВМЛflП ФУОfl ЛБ‡ˆЛЛ (Ф УВНˆЛЛ ПУПВМЪ‡ ЛПФЫО¸Т‡) М‡ ‡БОЛ˜М˚В М‡Ф ‡‚ОВМЛfl ‚ Ф УТЪ ‡МТЪ‚В (‚ Н‡˜ВТЪ‚В Ъ‡НЛı ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪУ‚ ПУКМУ, М‡Ф ЛПВ , ‚БflЪ¸ ЛБПВ ВМЛfl Ф УВНˆЛЛ ТФЛМ‡ М‡ УТЛ x, y Ë z). к‡ТТПУ- Ъ ЛП Ф УТЪУИ ЛОО˛ТЪ ‡ЪЛ‚М˚И ˜ЛТОВММ˚И Ф Л- ПВ . иЫТЪ¸ М‡Ф ‡‚ОВМЛВ ТФЛМ‡ ‡МТ‡П·Оfl ˝ОВНЪ У- МУ‚ Б‡‰‡ВЪТfl ФУОfl М˚ПЛ Ы„О‡ПЛ θ = ϕ = π /4. лУУЪ- ‚ВЪТЪ‚Ы˛˘ЛИ ЪУ˜М˚И ‚ВНЪУ ТУТЪУflМЛfl ВТЪ¸ (Щ‡БЫ ФВ ‚УИ НУПФУМВМЪ˚ П˚ ФУОУКЛОЛ ‡‚МУИ МЫО˛)
c( 0) |
|
0.924 |
|
= |
. |
||
|
|
0.271 + 0.271i |
|
è Ë ËÁÏ ÂÌËË Ô ÓÂ͈ËË ÒÔË̇ ̇ ÓÒ¸ x ‚В УflЪМУТЪ¸ Ф УВНˆЛЛ +1/2 ‡‚М‡ 0.75, ТУУЪ‚ВЪТЪ‚ВММУ ‚В УflЪМУТЪ¸ Ф УВНˆЛЛ –1/2 ‡‚М‡ 0.25. нВ КВ Т‡- П˚В ‚В УflЪМУТЪЛ УЪМУТflЪТfl Л Н Ф УВНˆЛЛ М‡ УТ¸ y. ÑÎfl Ô ÓÂ͈ËË Ì‡ ÓÒ¸ z ЛПВВП P (+1/2) = 0.854, P(− 1/2) = 0.146. иЫТЪ¸ ‚ Н‡К‰УП ЛБ М‡Ф ‡‚ОВМЛИ ЛБПВ ВМ˚ ТФЛМ˚ 100 ˝ОВНЪ УМУ‚ Л ФУОЫ˜ВМ˚ ТОВ- ‰Ы˛˘ЛВ ВБЫО¸Ъ‡Ъ˚: Nx(+1/2) = 80 (‚ПВТЪУ УКЛ‰‡- ВП˚ı 75), Nx(–1/2) = 20, Ny(+1/2) = 74 (‚ПВТЪУ УКЛ- ‰‡ВП˚ı 75), Ny(–1/2) = 26, Nz(+1/2) = 92 (‚ПВТЪУ УКЛ‰‡ВП˚ı 85.4), Nz(–1/2) = 8. иУ М‡·О˛‰‡ВП˚П ‰‡ММ˚П ПВЪУ‰УП П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl ‚ ТУУЪ‚ВЪТЪ‚ЛЛ Т и ЛОУКВМЛВП ПУКМУ ФУОЫ˜ЛЪ¸ УˆВМНЫ ‚ВНЪУ ‡ ТУТЪУflМЛfl
c |
|
0.939 |
|
= |
. |
||
|
|
0.271 + 0.212i |
|
лЪВФВМ¸ ·ОЛБУТЪЛ УˆВМНЛ Н ЪУ˜МУПЫ ‚ВНЪУ Ы ПУКМУ УˆВМЛЪ¸ Н‚‡‰ ‡ЪУП ПУ‰ЫОfl Лı ТН‡Оfl МУ„У
Ô ÓËÁ‚‰ÂÌËfl: |cc*(0)|2 = 0.99665 (Ô‡ ‡ÏÂÚ ıË-Í‚‡- ‰ ‡Ú ‡‚ÂÌ 1.0059, ÒÏ. ÌËÊ ÙÓ ÏÛÎÛ (23)).
ЗБ‡ЛПМУ ‰УФУОМЛЪВО¸М˚В ˝НТФВ ЛПВМЪ˚ ЫМЛ- Ъ‡ МУ Т‚flБ‡М˚ ПВК‰Ы ТУ·УИ. и Л ˝ЪУП ‚ Н‡К‰УП УЪ‰ВО¸МУП ˝НТФВ ЛПВМЪВ ЛБ ТУ‚УНЫФМУТЪЛ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı П˚ В„ЛТЪ Л ЫВП МВ ФТЛЩЫМНˆЛ˛, ‡ ЪУО¸НУ Н‚‡‰ ‡Ъ ВВ ПУ‰ЫОfl (Ъ.В. ‚В У- flЪМУТЪ¸ ЛОЛ ФОУЪМУТЪ¸ ‚В УflЪМУТЪЛ). С Ы„ЛПЛ ТОУ‚‡ПЛ, ‚ Н‡К‰УП УЪ‰ВО¸МУ ‚БflЪУП ˝НТФВ ЛПВМЪВ ЛБ ТУ‚УНЫФМУТЪЛ ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪУ‚ ‚В УflЪМУТЪМУВ (˜‡ТЪУЪМУВ) ФУ‚В‰В- МЛВ ТЛТЪВП˚ fl‚ОflВЪТfl ‚ФУОМВ НУОПУ„У У‚ТНЛП (Ъ.В. ТУУЪ‚ВЪТЪ‚ЫВЪ ‡НТЛУП‡ЪЛНВ ЪВУ ЛЛ ‚В УflЪМУТЪВИ дУОПУ„У У‚‡). зВНУОПУ„У У‚ТНЛИ ı‡ ‡Н- ЪВ Н‚‡МЪУ‚УИ ЪВУ ЛЛ Т‚flБ‡М ЛПВММУ Т УЪПВ˜ВММУИ ‚˚¯В ЫМЛЪ‡ МУИ Т‚flБ¸˛ ‡БОЛ˜М˚ı ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı НУОПУ„У У‚ТНЛı ‚В УflЪМУТЪМ˚ı Ф УТЪ ‡МТЪ‚.
е‡Ъ Лˆ‡ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡ Л ЪУ˜МУТЪ¸ ТЪ‡ЪЛТЪЛ˜ВТНУ„У УˆВМЛ‚‡МЛfl
èÛÒÚ¸ ÔÒË-ÙÛÌ͈Ëfl Á‡‚ËÒËÚ ÓÚ s ÌÂËÁ‚ÂÒÚÌ˚ı Ô‡ ‡ÏÂÚ Ó‚ c0, c1, …, cs – 1 (ТУ„О‡ТМУ Ъ ‡‰ЛˆЛЛ, ТЫ- ˘ВТЪ‚Ы˛˘ВИ ‚ Н‚‡МЪУ‚УИ ПВı‡МЛНВ, МЫПВ ‡ˆЛfl ·‡БЛТМ˚ı ЩЫМНˆЛИ У·˚˜МУ М‡˜ЛМ‡ВЪТfl Т МЫОВ‚У„У ˝ОВПВМЪ‡ – УТМУ‚МУ„У ТУТЪУflМЛfl). З‚В‰ВММ˚В Ф‡-‡ПВЪ ˚ fl‚Оfl˛ЪТfl НУ˝ЩЩЛˆЛВМЪ‡ПЛ ‡БОУКВМЛfl ФУ МВНУЪУ УПЫ М‡·У Ы ·‡БЛТМ˚ı ЩЫМНˆЛИ
ψ ( x) = |
s∑– 1 ci ϕ i ( x) . |
(4) |
|
i = 0 |
|
ЕЫ‰ВП Ф‡ ‡ООВО¸МУ ‡ТТП‡Ъ Л‚‡Ъ¸ ‰‚‡ ‡БОЛ˜М˚ı ТОЫ˜‡fl: ФТЛ-ЩЫМНˆЛfl fl‚ОflВЪТfl ‰ВИТЪ‚ЛЪВО¸МУИ ЛОЛ НУПФОВНТМУИ. З ФВ ‚УП ТОЫ˜‡В ЛПВВП ‰ВОУ Т ‰ВИТЪ‚ЛЪВО¸М˚П „ЛО¸·В ЪУ‚˚П Ф УТЪ ‡МТЪ‚УП, ‚У ‚ЪУ УП – Т НУПФОВНТМ˚П. З ФУТОВ‰МВП ТОЫ˜‡В ФТЛ-ЩЫМНˆЛfl fl‚ОflВЪТfl “Б‡ФЛТМУИ НМЛКНУИ М‡·О˛- ‰‡ЪВОfl”, Ф Л„У‰МУИ ‰Оfl У‰МУ‚ ВПВММУ„У УФЛТ‡МЛfl ‚ТВı ‚УБПУКМ˚ı ˝НТФВ ЛПВМЪ‡О¸М˚ı ЫТЪ‡МУ‚УН, ЫМЛЪ‡ МУ Т‚flБ‡ММ˚ı ‰ Ы„ Т ‰ Ы„УП. б‡ПВЪЛП, ˜ЪУ ‚ НУПФОВНТМУП „ЛО¸·В ЪУ‚УП Ф УТЪ ‡МТЪ‚В ˜ЛТОУ УˆВМЛ‚‡ВП˚ı ‚В˘ВТЪ‚ВММ˚ı Ф‡ ‡ПВЪ У‚ Щ‡НЪЛ- ˜ВТНЛ ‚ ‰‚‡ ‡Б‡ ·УО¸¯В, ˜ВП ‚ ‰ВИТЪ‚ЛЪВО¸МУП „ЛО¸·В ЪУ‚УП Ф УТЪ ‡МТЪ‚В ЪУИ КВ ‡БПВ МУТЪЛ.
и В‰ФУОУКЛП, ˜ЪУ М‡·У ЩЫМНˆЛИ fl‚ОflВЪТfl У ЪУМУ ПЛ У‚‡ММ˚П. нУ„‰‡ ЫТОУ‚ЛВ МУ ПЛ У‚НЛ ФУОМУИ ‚В УflЪМУТЪЛ М‡ В‰ЛМЛˆЫ ·Ы‰ВЪ ЛПВЪ¸ ‚Л‰
ci ci* = 1. |
(5) |
б‰ВТ¸ Л ‰‡ОВВ ‰У„У‚У ЛПТfl, ˜ЪУ ФУ ФУ‚ЪУ fl˛˘ЛПТfl ЛМ‰ВНТ‡П, МЫПВ Ы˛˘ЛП ˜ОВМ˚ ‡БОУКВМЛfl ФУ М‡·У Ы ·‡БЛТМ˚ı ЩЫМНˆЛИ, Ф В‰ФУО‡„‡ВЪТfl ТЫППЛ У‚‡МЛВ (ВТОЛ МВ У„У‚У ВМУ У· ‡ЪМУВ). лЪ‡ЪЛТЪЛ˜ВТНЛВ ТЫПП˚, Т‚flБ‡ММ˚В Т ТЫППЛ У‚‡МЛВП ФУ ˝ОВПВМЪ‡П ‚˚·У НЛ, ·Ы‰ВП ‚˚ФЛТ˚‚‡Ъ¸ fl‚МУ. СОfl
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004 |
3* |

740 |
ÅÓ„‰‡ÌÓ‚ |
Ф УТЪУЪ˚ ‚М‡˜‡ОВ ‡ТТП‡Ъ Л‚‡ВЪТfl ТОЫ˜‡И, НУ„‰‡ ФТЛ-ЩЫМНˆЛfl fl‚ОflВЪТfl ‰ВИТЪ‚ЛЪВО¸МУИ. иЫТЪ¸‡БОУКВМЛВ ЛПВВЪ ‚Л‰
ψ ( x) = 1 – ( c12 + … + c2s – 1) ϕ 0 ( x) + c1 ϕ 1 ( x) +…
(6)
… + cs – 1 ϕ s – 1 ( x) .
á‰ÂÒ¸ Ï˚ ËÒÍβ˜ËÎË ËÁ ˜ËÒ· ÓˆÂÌË‚‡ÂÏ˚ı Ô‡ ‡-
ÏÂÚ Ó‚ ÍÓ˝ÙÙˈËÂÌÚ c0 = 1 – ( c12 + … + c2s – 1) ,
Ú‡Í Í‡Í Òӄ·ÒÌÓ ÛÒÎӂ˲ ÌÓ ÏË Ó‚ÍË, ÓÌ ‚˚ ‡- ʇÂÚÒfl ˜Â ÂÁ ‰ Û„Ë ÍÓ˝ÙÙˈËÂÌÚ˚. è‡ ‡ÏÂÚ ˚ c1, c2, …, cs – 1 МВБ‡‚ЛТЛП˚. аı ‡ТЛПФЪУЪЛ˜ВТНЛВ Т‚УИТЪ‚‡ ЛБЫ˜ЛП Т ЛТФУО¸БУ‚‡МЛВП ЛМЩУ П‡ˆЛУММУИ П‡Ъ Лˆ˚ оЛ¯В ‡ [16]
Iij ( c) |
∂ ln p( x, c) ∂ ln p( x, c) |
(7) |
|
= n∫ ------------------------- ------------------------- p( x, c) dx. |
|||
|
∂ ci |
∂ c j |
|
оЫМ‰‡ПВМЪ‡О¸МУВ БМ‡˜ВМЛВ П‡Ъ Лˆ˚ оЛ¯В ‡ Т‚flБ‡МУ Т ВВ Т‚УИТЪ‚УП УФ В‰ВОflЪ¸ „ ‡МЛˆЫ ЪУ˜- МУТЪЛ ТЪ‡ЪЛТЪЛ˜ВТНЛı УˆВМУН, НУЪУ ‡fl ‚ МВНУЪУ-УП ТП˚ТОВ ı‡ ‡НЪВ ЛБЫВЪ М‡ЛОЫ˜¯Ы˛ ЪУ˜МУТЪ¸, НУЪУ ‡fl ПУКВЪ ·˚Ъ¸ ‰УТЪЛ„МЫЪ‡ ‚ Ф ЛМˆЛФВ. лУ- „О‡ТМУ Ъ‡Н М‡Б˚‚‡ВПУПЫ МВ ‡‚ВМТЪ‚Ы к‡У–д ‡ПВ-‡–о В¯В [16], ‰Оfl О˛·УИ МВТПВ˘ВММУИ УˆВМНЛ
θˆ МВЛБ‚ВТЪМУ„У ПМУ„УПВ МУ„У Ф‡ ‡ПВЪ ‡ θ П‡Ъ-
ˈ‡ Σ( θˆ) – I–1(θ ) fl‚ОflВЪТfl МВУЪ Лˆ‡ЪВО¸МУ УФ В- ‰ВОВММУИ. б‰ВТ¸ Σ( θˆ) – ÍÓ‚‡ ˇˆËÓÌ̇fl Ï‡Ú Ëˆ‡
ÓˆÂÌÍË θˆ . СОfl УˆВМУН ФУ ПВЪУ‰Ы П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl ТУУЪ‚ВЪТЪ‚Ы˛˘‡fl ‡БМЛˆ‡ ‡ТЛПФЪУЪЛ˜ВТНЛ Т‚У‰ЛЪТfl Н МЫОВ‚УИ П‡Ъ ЛˆВ (Т‚УИТЪ‚У ‡ТЛПФЪУЪЛ˜ВТНУИ ˝ЩЩВНЪЛ‚МУТЪЛ).
СОfl ˆВОВИ М‡ТЪУfl˘ВИ ‡·УЪ˚ У˜ВМ¸ ‚‡КМУ, ˜ЪУ ‚˚ ‡КВМЛВ ‰Оfl ЛМЩУ П‡ˆЛУММУИ П‡Ъ Лˆ˚ оЛ¯В-‡ ‡‰ЛН‡О¸МУ ЫФ У˘‡ВЪТfl, ВТОЛ ‚‚ВТЪЛ ФТЛ-ЩЫМН- ˆЛ˛:
Iij |
= 4n∫ ∂ψ--------(---x---,---c--)- ∂ψ------- |
-(---x---,---c--)-dx. |
(8) |
|
∂ ci |
∂ c j |
|
З ТОЫ˜‡В ‡БОУКВМЛfl (6) ЛМЩУ П‡ˆЛУММ‡fl П‡Ъ Л-
ˆ‡ Iij ЛПВВЪ ФУ fl‰УН (s – 1) × (s – 1) Л ‚˚ ‡К‡ВЪТfl ‚ ТОВ‰Ы˛˘ВП Ф УТЪУП ‚Л‰В:
Iij = |
4n |
|
c c |
|
|
δ ij + ---i-----j |
, |
(9) |
|||
|
|
|
2 |
|
|
|
|
|
c0 |
|
|
„‰Â c0 = 1 – ( c12 + … |
+ cs2 |
– 1) ; i, j = 1, …, s – 1. |
|||
á‡Ï˜‡ÚÂθÌÓÈ |
УТУ·ВММУТЪ¸˛ |
ÔÓÎÛ˜ÂÌÌÓ„Ó |
|||
‚˚ ‡КВМЛfl fl‚ОflВЪТfl В„У МВБ‡‚ЛТЛПУТЪ¸ УЪ ‚˚·У-‡ ·‡БЛТМ˚ı ЩЫМНˆЛИ. б‡ПВЪЛП, ˜ЪУ ЪУО¸НУ Ф В‰- ТЪ‡‚ОВМЛВ ФОУЪМУТЪЛ ‚ ‚Л‰В p = |ψ| 2 Ф Л‚У‰ЛЪ Н ЫМЛ‚В Т‡О¸МУИ (Л Ф УТЪВИ¯ВИ) ТЪ ЫНЪЫ В П‡Ъ Л- ˆ˚ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡.
З ТЛОЫ ‡ТЛПФЪУЪЛ˜ВТНУИ ˝ЩЩВНЪЛ‚МУТЪЛ ПВЪУ- ‰‡ П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl П‡Ъ Лˆ‡ НУ‚‡-
Л‡ˆЛИ УˆВМНЛ ‚ВНЪУ ‡ ТУТЪУflМЛfl ВТЪ¸ П‡Ъ Лˆ‡, У· ‡ЪМ‡fl П‡Ъ ЛˆВ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡,
ˆ |
–1 |
( c) . |
(10) |
Σ ( c) = I |
|
к‡Т¯Л ЛП ЪВФВ ¸ ФУОЫ˜ВММЫ˛ П‡Ъ ЛˆЫ НУ‚‡ Л‡- ˆЛИ, ‰У·‡‚Л‚ ‚ МВВ НУ‚‡ Л‡ˆЛЛ НУПФУМВМЪ˚ c0 ‚ВНЪУ ‡ ТУТЪУflМЛfl Т УТЪ‡О¸М˚ПЛ НУПФУМВМЪ‡ПЛ. З ВБЫО¸Ъ‡ЪВ ФУОЫ˜ЛП ‰Оfl НУПФУМВМЪ П‡Ъ Лˆ˚ НУ‚‡ Л‡ˆЛИ
Σ ij = ij – ci c j) i, j = 0, 1, … , s – 1. (11)
л „ВУПВЪ Л˜ВТНУИ ЪУ˜НЛ Б ВМЛfl П‡Ъ Лˆ‡ НУ‚‡ Л- ‡ˆЛИ (11) fl‚ОflВЪТfl ЪВМБУ УП ‚ЪУ У„У ‡М„‡. ЕУОВВ ЪУ„У, ФУОЫ˜ВММ‡fl П‡Ъ Лˆ‡ НУ‚‡ Л‡ˆЛИ fl‚ОflВЪТfl Т ЪУ˜МУТЪ¸˛ ‰У ПМУКЛЪВОfl В‰ЛМТЪ‚ВММ˚П ЪВМБУ-УП ‚ЪУ У„У ‡М„‡, Ы‰У‚ОВЪ‚У fl˛˘ЛП ЫТОУ‚Л˛ МУ ПЛ У‚НЛ. е‡Ъ Лˆ‡
ρ ij = ci c j |
(12) |
М‡Б˚‚‡ВЪТfl ‚ Н‚‡МЪУ‚УИ ПВı‡МЛНВ П‡Ъ ЛˆВИ ФОУЪМУТЪЛ (˜ЛТЪУ„У ТУТЪУflМЛfl). н‡НЛП У· ‡БУП,
Σ |
= |
1 |
( E – ρ ) , |
(13) |
4n |
||||
|
|
----- |
|
|
„‰Â E – ‰ËÌ˘̇fl Ï‡Ú Ëˆ‡ ÔÓ fl‰Í‡ s × s. З ‰Л‡„У- М‡О¸МУП Ф В‰ТЪ‡‚ОВМЛЛ
Σ = UDU+ , (14)
„‰Â U – ÛÌËÚ‡ ̇fl (Ó ÚÓ„Ó̇θ̇fl) Ï‡Ú Ëˆ‡, D – ‰Ë‡„Ó̇θ̇fl Ï‡Ú Ëˆ‡.
д‡Н ЛБ‚ВТЪМУ ЛБ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ, ‚ ‰Л‡„У- М‡О¸МУП Ф В‰ТЪ‡‚ОВМЛЛ П‡Ъ Лˆ‡ ФОУЪМУТЪЛ ˜ЛТЪУ- „У ТУТЪУflМЛfl ЛПВВЪ ЪУО¸НУ У‰ЛМ МВМЫОВ‚УИ ( ‡‚- М˚И В‰ЛМЛˆВ) ˝ОВПВМЪ. н‡НЛП У· ‡БУП, ‚ М‡¯ВП ТОЫ˜‡В ‰Л‡„УМ‡О¸ П‡Ъ Лˆ˚ D ЛПВВЪ У‰ЛМ ˝ОВПВМЪ,‡‚М˚И МЫО˛ (ТУУЪ‚ВЪТЪ‚Ы˛˘ЛИ ВПЫ ТУ·ТЪ‚ВММ˚И ‚ВНЪУ ВТЪ¸ ‚ВНЪУ ТУТЪУflМЛfl), ‡ УТЪ‡О¸М˚В ˝ОВПВМЪ˚ ‰Л‡„УМ‡ОЛ ‡‚М˚ 1/4n (ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ ЛП ТУ·ТЪ‚ВММ˚В ‚ВНЪУ ˚ Л Лı ‚ТВ‚УБПУКМ˚В ОЛМВИ- М˚В НУП·ЛМ‡ˆЛЛ У· ‡БЫ˛Ъ ФУ‰Ф УТЪ ‡МТЪ‚У, fl‚Оfl- ˛˘ВВТfl У ЪУ„УМ‡О¸М˚П ‰УФУОМВМЛВП Н ‚ВНЪУ Ы ТУТЪУflМЛfl). з‡ОЛ˜ЛВ МЫОВ‚У„У ˝ОВПВМЪ‡ М‡ „О‡‚- МУИ ‰Л‡„УМ‡ОЛ ФУН‡Б˚‚‡ВЪ, ˜ЪУ У· ‡ЪМ‡fl П‡Ъ Лˆ‡ (Ъ.В. П‡Ъ Лˆ‡ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡ s-„У ФУ fl‰Н‡) МВ ТЫ˘ВТЪ‚ЫВЪ, ˜ЪУ ФУМflЪМУ, Ъ‡Н Н‡Н ‚ ‡ТФ В‰ВОВМЛЛ ЛПВВЪТfl ‚ТВ„У s – 1 ÌÂÁ‡‚ËÒËÏ˚È Ô‡ ‡ÏÂÚ .
иУОЫ˜ВММ˚В ВБЫО¸Ъ‡Ъ˚ УЪМУТЛЪВО¸МУ ТЪ‡ЪЛТЪЛ˜ВТНЛı Т‚УИТЪ‚ ‚УТТЪ‡МУ‚ОВММУ„У ПВЪУ‰УП П‡Н- ТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl ‚ВНЪУ ‡ ТУТЪУflМЛfl ПУ„ЫЪ ·˚Ъ¸ ВБ˛ПЛ У‚‡М˚ ТОВ‰Ы˛˘ЛП У· ‡БУП. ЗУТТЪ‡МУ‚ОВММ˚И ‚ВНЪУ ТУТЪУflМЛfl УЪОЛ˜‡ВЪТfl УЪ ЛТЪЛММУ„У ЪВП, ˜ЪУ Б‡¯ЫПОВМ ФУТ В‰ТЪ‚УП ТОЫ- ˜‡ИМУ„У ‚ВНЪУ ‡ У¯Л·НЛ, ‡ТФУОУКВММУ„У ‚ Ф У- ТЪ ‡МТЪ‚В, У ЪУ„УМ‡О¸МУП ЛТЪЛММУПЫ ‚ВНЪУ Ы ТУТЪУflМЛfl. дУПФУМВМЪ˚ ‚ВНЪУ ‡ У¯Л·НЛ (‚ТВ„У s – 1 НУПФУМВМЪ‡) ВТЪ¸ ‡ТЛПФЪУЪЛ˜ВТНЛ МУ П‡О¸М˚В
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004
|
|
|
йТМУ‚М˚В ФУМflЪЛfl НО‡ТТЛ˜ВТНУИ Л Н‚‡МЪУ‚УИ ТЪ‡ЪЛТЪЛНЛ |
741 |
||||||||||||||||||||||||
ÌÂÁ‡‚ËÒËÏ˚ ÒÎÛ˜‡ÈÌ˚ ‚Â΢ËÌ˚ Ò Ó‰ÌÓÈ Ë ÚÓÈ |
й¯Л·Н‡ ‡ФФ УНТЛП‡ˆЛЛ |
|
|
|||||||||||||||||||||||||
Ê ‰ËÒÔ ÒËÂÈ 1/4n. Ç |
Û͇Á‡ÌÌÓÏ s – 1-Ï ÌÓÏ |
0.004 |
|
|
|
|
||||||||||||||||||||||
ФУ‰Ф УТЪ ‡МТЪ‚В ‚ВНЪУ У¯Л·НЛ ЛПВВЪ ЛБУЪ УФ- |
|
|
|
|
|
|||||||||||||||||||||||
МУВ М‡Ф ‡‚ОВМЛВ Л В„У Н‚‡‰ ‡Ъ ‰ОЛМ˚ ВТЪ¸ ТОЫ˜‡И- |
0.002 |
|
|
|
|
|||||||||||||||||||||||
̇fl ‚Â΢Ë̇ χ |
s2 |
– 1 /4n, „‰Â χ |
s2 |
– 1 – ÒÎÛ˜‡È̇fl ‚ÂÎË- |
|
2 |
|
|
||||||||||||||||||||
˜ЛМ‡, ЛПВ˛˘‡fl ‡ТФ В‰ВОВМЛВ ıЛ-Н‚‡‰ ‡Ъ Т s – 1 |
|
|
|
|
||||||||||||||||||||||||
ТЪВФВМ¸˛ Т‚У·У‰˚, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
1 – ( cc |
( 0) |
) |
2 |
|
= |
2 |
|
|
|
|
|
|
|
|
|
(15) |
|
1 |
|
|
|
||||
|
|
|
|
|
|
χ s – 1 /4n. |
|
|
|
|
|
–0.002 |
|
|
|
|
||||||||||||
иУТОВ‰МВВ ‚˚ ‡КВМЛВ УБМ‡˜‡ВЪ, ˜ЪУ Н‚‡‰ ‡Ъ ТН‡- |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
Оfl МУ„У Ф УЛБ‚В‰ВМЛfl ЛТЪЛММУ„У Л ‚УТТЪ‡МУ‚ОВМ- |
–0.004 |
|
|
|
|
|||||||||||||||||||||||
ÌÓ„Ó ‚ÂÍÚÓ Ó‚ |
|
ТУТЪУflМЛИ |
ÏÂ̸¯Â |
|
‰ËÌˈ˚ |
̇ |
|
20 |
40 |
|
||||||||||||||||||
‡ТЛПФЪУЪЛ˜ВТНЛ |
|
χÎÛ˛ |
ÒÎÛ˜‡ÈÌÛ˛ |
‚Â΢ËÌÛ |
0 |
|
|
|||||||||||||||||||||
|
|
|
|
n1 |
|
|||||||||||||||||||||||
χ s2 – 1 /4n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
è ‰ÒÚ‡‚ÎÂÌÌ˚ ÂÁÛθڇÚ˚ ÔÓÁ‚ÓÎfl˛Ú ‚‚ÂÒ- |
êËÒ. 3. л ‡‚МВМЛВ ЪУ˜МУТЪЛ НУ МВ‚УИ УˆВМНЛ (1) Ë ÚÂÓ- |
|||||||||||||||||||||||||||
ЪЛ МУ‚Ы˛ ТЪ‡ЪЛТЪЛ˜ВТНЫ˛ ı‡ ‡НЪВ ЛТЪЛНЫ – ‰У‚В- |
ÂÏ˚ åÛ‡‚ ‡–ã‡Ô·҇ (2) Ф Л ‡ФФ УНТЛП‡ˆЛЛ ·ЛМУПЛ- |
|||||||||||||||||||||||||||
‡О¸МУ„У ‡ТФ В‰ВОВМЛfl МУ П‡О¸М˚П (n = 100, p1 = 0.2). |
||||||||||||||||||||||||||||
ЛЪВО¸М˚И НУМЫТ (‚ПВТЪУ Ъ ‡‰ЛˆЛУММУ„У ‰У‚В Л- |
||||||||||||||||||||||||||||
ÚÂθÌÓ„Ó ËÌÚ ‚‡Î‡). èÛÒÚ¸ ϑ |
– Û„ÓÎ ÏÂÊ‰Û ÌÂËÁ- |
|
|
|
|
|
||||||||||||||||||||||
‚ВТЪМ˚П ЛТЪЛММ˚П ‚ВНЪУ УП ТУТЪУflМЛfl Ò(0) Ë |
Лfl ıЛ-Н‚‡‰ ‡Ъ ‚ ЩУ ПВ (17) (‚ ‡ТЛПФЪУЪЛ˜ВТНУП |
|||||||||||||||||||||||||||
‚ВНЪУ УП ТУТЪУflМЛfl c, ‚ÓÒÒÚ‡ÌÓ‚ÎÂÌÌ˚Ï Ì‡ ÓÒÌÓ- |
Ô Â‰ÂÎÂ). |
|
|
|
|
|||||||||||||||||||||||
‚ ¯ÂÌËfl Û ‡‚ÌÂÌËfl Ô ‡‚‰ÓÔÓ‰Ó·Ëfl (ÒÏ. è ËÎÓ- |
ëÎÛ˜‡È s |
= 2 ТУУЪ‚ВЪТЪ‚ЫВЪ ·ЛМУПЛ‡О¸МУПЫ |
||||||||||||||||||||||||||
КВМЛВ). нУ„‰‡ |
‰Îfl |
ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘Â„Ó |
|
Í‚‡‰ ‡Ú‡ |
||||||||||||||||||||||||
|
‡ТФ В‰ВОВМЛ˛. З ˝ЪУП ТОЫ˜‡В НУ МВ‚УИ ПВЪУ‰ |
|||||||||||||||||||||||||||
ТЛМЫТ‡ Ы„О‡ ПУКМУ Б‡ФЛТ‡Ъ¸ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
‰‡ВЪ ТОВ‰Ы˛˘ВВ ТУУЪМУ¯ВМЛВ ‰Оfl ‡ФФ УНТЛП‡ˆЛЛ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
ϑ |
|
|
|
|
|
2 |
ϑ |
= 1 – ( cc |
( 0) |
) |
2 |
= |
|
|
|
|
·ЛМУПЛ‡О¸МУ„У ‡ТФ В‰ВОВМЛfl МУ П‡О¸М˚П: |
|
||||||||
sin |
= 1 – cos |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
χ |
s2 – 1 |
≤ |
χ |
s2 – 1, α |
|
|
|
|
|
|
|
(16) |
2( |
n1 p2 – |
n2 p1) N ( 0, 1) . |
(18) |
|||||||
|
|
|
|
= |
---------- |
-------------- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4n |
|
|
4n . |
|
|
|
|
|
|
|
|
á‰ÂÒ¸ p1 + p2 = 1, n1 + n2 = n, N(0, 1) – ÒÎÛ˜‡È̇fl ‚Â- |
|||||||||||
á‰ÂÒ¸ χ s2 |
– 1, α – Í‚‡ÌÚËθ, Óڂ˜‡˛˘‡fl Û Ó‚Ì˛ Á̇- |
΢Ë̇, Ëϲ˘‡fl ÌÓ Ï‡Î¸ÌÓ |
‡ТФ В‰ВОВМЛВ Т |
|||||||||||||||||||||||||
˜ЛПУТЪЛ α |
|
‰Оfl ‡ТФ В‰ВОВМЛfl ıЛ-Н‚‡‰ ‡Ъ Т s – 1 |
ÌÛ΂˚Ï Ò Â‰ÌËÏ Ë Â‰ËÌ˘ÌÓÈ ‰ËÒÔ ÒËÂÈ. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
ТЪВФВМ¸˛ Т‚У·У‰˚. еМУКВТЪ‚У М‡Ф ‡‚ОВМЛИ, Б‡- |
ДМ‡ОУ„Л˜М˚И ВБЫО¸Ъ‡Ъ НО‡ТТЛ˜ВТНУИ ЪВУ ЛЛ |
|||||||||||||||||||||||||||
‰‡‚‡ÂÏ˚ı |
|
Ì ‡‚ÂÌÒÚ‚ÓÏ |
(16), Ó· ‡ÁÛÂÚ |
|
‰Ó‚Â Ë- |
‚В УflЪМУТЪВИ (ЪВУ ВП‡ еЫ‡‚ ‡–г‡ФО‡Т‡) ‚˚„Оfl- |
||||||||||||||||||||||
ЪВО¸М˚И НУМЫТ. йТ¸˛ ‰У‚В ЛЪВО¸МУ„У НУМЫТ‡ ТОЫ- |
‰ËÚ ÒÎÂ‰Û˛˘ËÏ Ó· ‡ÁÓÏ [16]: |
|
|
|||||||||||||||||||||||||
КЛЪ ‚УТТЪ‡МУ‚ОВММ˚И ‚ВНЪУ ТУТЪУflМЛfl c. ÑÓ‚Â- |
|
n1 – n p1 |
|
|
||||||||||||||||||||||||
ËÚÂθÌ˚È |
НУМЫТ Ф ВТОВ‰ЫВЪ ˆВО¸ |
ÔÓÍ ˚Ú¸ |
Ò |
|
|
|
||||||||||||||||||||||
Б‡‰‡ММУИ ‰У‚В ЛЪВО¸МУИ ‚В УflЪМУТЪ¸˛ P = 1 – α |
|
------------------- N ( 0, 1) . |
|
(19) |
||||||||||||||||||||||||
М‡Ф ‡‚ОВМЛВ МВЛБ‚ВТЪМУ„У |
|
|
‚ВНЪУ ‡ ТУТЪУflМЛfl. |
|
n p1 p2 |
|
|
|||||||||||||||||||||
äÓ Ì‚‡fl ÓˆÂÌ͇ ‰‡ÂÚ ÛÚÓ˜ÌÂÌÌ˚Â Ô Â‰ÒÚ‡‚ÎÂÌËfl |
çÂÚ Û‰ÌÓ Û·Â‰ËÚ¸Òfl, ˜ÚÓ ÙÓ ÏÛ· (19) fl‚ÎflÂÚÒfl |
|||||||||||||||||||||||||||
‰Îfl Ú‡ÍËı Í·ÒÒ˘ÂÒÍËı ÂÁÛθڇÚÓ‚, Í‡Í Í ËÚÂ- |
||||||||||||||||||||||||||||
ÒΉÒÚ‚ËÂÏ |
ÙÓ ÏÛÎ˚ (18) (‚ |
‡ТЛПФЪУЪЛ˜ВТНУП |
||||||||||||||||||||||||||
ЛИ ıЛ-Н‚‡‰ ‡Ъ Л ‡ФФ УНТЛП‡ˆЛfl ·ЛМУПЛ‡О¸МУ„У |
||||||||||||||||||||||||||||
Ô Â‰ÂÎÂ). Ç ÚÓ Ê ‚ ÂÏfl Ô Ë ÍÓ̘Ì˚ı Ó·˙Âχı |
||||||||||||||||||||||||||||
‡ТФ В‰ВОВМЛfl „‡ЫТТУ‚˚П. иЫТЪ¸ p1, p2, …, ps – ÚÂ- |
||||||||||||||||||||||||||||
‚˚·У НЛ ‡ФФ УНТЛП‡ˆЛfl (18) ‰‡ВЪ ОЫ˜¯ВВ Ф Л- |
||||||||||||||||||||||||||||
У ВЪЛ˜ВТНЛВ ‚В УflЪМУТЪЛ, ‡ n1, n2, …, ns – ̇·Î˛- |
||||||||||||||||||||||||||||
·ОЛКВМЛВ ФУ Т ‡‚МВМЛ˛ Т НО‡ТТЛ˜ВТНЛП ВБЫО¸- |
||||||||||||||||||||||||||||
‰‡‚¯ËÂÒfl ˜ËÒ· ÔÓÔ‡‰‡ÌËÈ ÚÓ˜ÂÍ ‚ ÒÓÓÚ‚ÂÚÒÚ‚Û˛- |
||||||||||||||||||||||||||||
Ú‡ÚÓÏ (19) (‚ Ô ËÏ  ̇ ËÒ. 3 Ò Â‰Ìflfl ‡·ÒÓβÚ- |
||||||||||||||||||||||||||||
˘Ë ËÌÚ ‚‡Î˚. íÓ„‰‡ ÍÓ Ì‚‡fl ÙÓ Ï‡ ‰Îfl Í Ë- |
||||||||||||||||||||||||||||
М‡fl У¯Л·Н‡ НУ МВ‚УИ ‡ФФ УНТЛП‡ˆЛЛ УН‡Б‡О‡Т¸ ‚ |
||||||||||||||||||||||||||||
Ú Ëfl ıË-Í‚‡‰ ‡Ú ·Û‰ÂÚ ËÏÂÚ¸ ‚ˉ [6] |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
1.82 ‡Á‡ ÏÂ̸¯ÂÈ ÒÓÓÚ‚ÂÚÒÚ‚Û˛˘ÂÈ Ó¯Ë·ÍË |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4[ n – ( |
n1 p1 + |
|
n2 p2 + … |
+ |
|
|
ns ps) 2] |
|
= χ |
|
s2 |
– 1 . (17) |
ÙÓ ÏÛÎ˚ åÛ‡‚ ‡–ã‡Ô·҇). |
|
|
|||||||||||||
З˚ ‡КВМЛВ (17) УБМ‡˜‡ВЪ, ˜ЪУ ВТОЛ МЫОВ‚‡fl „ЛФУ- |
и Л УФЛТ‡МЛЛ Н‚‡МЪУ‚˚ı ˝НТФВ ЛПВМЪУ‚ ·Ы‰ВП |
|||||||||||||||||||||||||||
‰Оfl УФ В‰ВОВММУТЪЛ ‡ТТП‡Ъ Л‚‡Ъ¸ ТОЫ˜‡И ‚Б‡ЛП- |
||||||||||||||||||||||||||||
ЪВБ‡ ТФ ‡‚В‰ОЛ‚‡, Ъ.В. ‡ТФ В‰ВОВМЛВ ‚В УflЪМУТ- |
МУ ‰УФУОМЛЪВО¸М˚ı НУУ ‰ЛМ‡ЪМ˚ı Л ЛПФЫО¸ТМ˚ı |
|||||||||||||||||||||||||||
ЪВИ ТУУЪ‚ВЪТЪ‚ЫВЪ ЪВУ ВЪЛ˜ВТНУПЫ |
|
‡ÒÔ Â‰ÂÎÂ- |
ЛБПВ ВМЛИ. и В‰ФУОУКЛП, ˜ЪУ |
‚ ÍÓÓ ‰Ë̇ÚÌÓÏ |
||||||||||||||||||||||||
Ì˲, ÚÓ ÒÚÓfl˘‡fl Ò΂‡ ‚Â΢Ë̇ ÂÒÚ¸ ÒÎÛ˜‡È̇fl |
Ô ÓÒÚ ‡ÌÒÚ‚Â Ô Ó‚Â‰ÂÌÓ n, ‡ ‚ ЛПФЫО¸ТМУП – m ËÁ- |
|||||||||||||||||||||||||||
‚ВОЛ˜ЛМ‡, ЛПВ˛˘‡fl ‡ТФ В‰ВОВМЛВ ıЛ-Н‚‡‰ ‡Ъ Т |
Ï ÂÌËÈ. å‡Ú ˈ‡ ËÌÙÓ Ï‡ˆËË î˯ ‡ ÓÔ Â‰ÂÎfl- |
|||||||||||||||||||||||||||
s – 1 ТЪВФВМ¸˛ Т‚У·У‰˚. лЪ‡М‰‡ ЪМ‡fl ЩУ П‡ Н Л- |
ÂÚÒfl ÒÛÏχ ÌÓÈ ËÌÙÓ Ï‡ˆËÂÈ, ÒӉ ʇ˘ÂÈÒfl ‚Ó |
|||||||||||||||||||||||||||
Ú Ëfl ıË-Í‚‡‰ ‡Ú [16] fl‚ÎflÂÚÒfl ÒΉÒÚ‚ËÂÏ Í ËÚÂ- |
‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪ‡ı (Т . Т (9)), |
|||||||||||||||||||||||||||
йинадД а лиЦднкйлдйиаь |
ÚÓÏ 96 |
|
|
‹ 5 |
2004 |
|
|
|
|
|||||||||||||||||||

742 |
ÅÓ„‰‡ÌÓ‚ |
Iij = ( n + m) |
|
δ |
|
ci c*j |
i, j |
= 1, … , s – 1, (20) |
||
|
ij |
+ --------- |
||||||
|
|
|
|
|
c0 |
2 |
|
|
„‰Â |c0| = 1 – ( |
c1 |
2 + … |
+ cs – 1 |
2) . б‡ПВЪЛП, ˜ЪУ ‚ |
||||
ЩУ ПЫОВ (20) ФУ Т ‡‚МВМЛ˛ Т ‡М‡ОУ„Л˜МУИ ЩУ - ПЫОУИ (9) УЪТЫЪТЪ‚ЫВЪ ПМУКЛЪВО¸, ‡‚М˚И 4. лУУЪ‚ВЪТЪ‚Ы˛˘ВВ ЫПВМ¸¯ВМЛВ ЛМЩУ П‡ˆЛЛ Т‚flБ‡МУ Т ЪВП, ˜ЪУ ЪВФВ ¸ Ф Л УˆВМЛ‚‡МЛЛ Ф‡ ‡ПВЪ У‚ МВ- У·ıУ‰ЛПУ УЪОЛ˜‡Ъ¸ ‰ Ы„ УЪ ‰ Ы„‡ НУ˝ЩЩЛˆЛВМЪ˚‡БОУКВМЛfl c Ë c*.
й· ‡˘ВМЛВ П‡Ъ Лˆ˚ оЛ¯В ‡ ‰‡ВЪ ЫТВ˜ВММЫ˛ (·ВБ МЫОВ‚УИ НУПФУМВМЪ˚) П‡Ъ ЛˆЫ НУ‚‡ Л‡ˆЛИ. З˚˜ЛТОflfl fl‚МУ НУ‚‡ Л‡ˆЛЛ, ТУ‰В К‡˘ЛВ МЫОВ‚Ы˛ НУПФУМВМЪЫ, ФУОЫ˜ЛП ‚ ВБЫО¸Ъ‡ЪВ ‰Оfl ФУОМУИ П‡- Ъ Лˆ˚ НУ‚‡ Л‡ˆЛИ УˆВМУН ‚˚ ‡КВМЛВ, ‡М‡ОУ„Л˜- МУВ (11),
Σ ij = δ ci δ c*j = |
1 |
( δ ij – ci c*j ) , |
|
(---n----+-----m----)- |
(21) |
i, j = 0, 1, … , s – 1.
е‡Ъ Лˆ‡ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡ Л П‡Ъ Лˆ‡ НУ‚‡ Л- ‡ˆЛИ fl‚Оfl˛ЪТfl ˝ ПЛЪУ‚˚ПЛ. оУ ПЫОЫ (21), У˜В- ‚Л‰МУ, ПУКМУ Б‡ФЛТ‡Ъ¸ ‚ ‚Л‰В
Σ |
= |
1 |
( E – ρ ) , |
(22) |
( n + m) |
||||
|
|
----------------- |
|
|
„‰Â E – ‰ËÌ˘̇fl Ï‡Ú Ëˆ‡ ÔÓ fl‰Í‡ s × s, ρ – П‡Ъ-Лˆ‡ ФОУЪМУТЪЛ (˜ЛТЪУ„У ТУТЪУflМЛfl). З ‰Л‡„У- М‡О¸МУП Ф В‰ТЪ‡‚ОВМЛЛ Σ = UDU+, „‰Â U – ÛÌËÚ‡ - ̇fl Ï‡Ú Ëˆ‡, D – ‰Ë‡„Ó̇θ̇fl Ï‡Ú Ëˆ‡. Ñˇ„Ó- ̇θ Ï‡Ú Ëˆ˚ D ЛПВВЪ У‰ЛМ ˝ОВПВМЪ, ‡‚М˚И МЫО˛ (ТУУЪ‚ВЪТЪ‚Ы˛˘ЛИ ВПЫ ТУ·ТЪ‚ВММ˚И ‚ВНЪУ ВТЪ¸ ‚ВНЪУ ТУТЪУflМЛfl), ‡ УТЪ‡О¸М˚В ˝ОВПВМЪ˚ ‰Л‡„УМ‡ОЛ ‡‚М˚ 1/(n + m) (ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ ЛП ТУ·ТЪ‚ВММ˚В ‚ВНЪУ ˚ Л Лı ‚ТВ‚УБПУКМ˚В ОЛМВИ- М˚В НУП·ЛМ‡ˆЛЛ У· ‡БЫ˛Ъ ФУ‰Ф УТЪ ‡МТЪ‚У, fl‚- Оfl˛˘ВВТfl У ЪУ„УМ‡О¸М˚П ‰УФУОМВМЛВП Н ‚ВНЪУ-Ы ТУТЪУflМЛfl).
д ЛЪВ ЛИ ıЛ-Н‚‡‰ ‡Ъ, ‰‡˛˘ЛИ ПВ Ы ·ОЛБУТЪЛ Н В‰ЛМЛˆВ ТН‡Оfl МУ„У Ф УЛБ‚В‰ВМЛfl ‚УТТЪ‡МУ‚- ОВММУ„У Л ЛТЪЛММУ„У ‚ВНЪУ У‚ ÒÒ*(0) Ë ‡Ì‡Îӄ˘- Ì˚È Í ËÚ ˲ (15), Á‡ÔËÒ˚‚‡ÂÚÒfl ‚ ‚ˉÂ
( n + m) ( 1 – |
|
cc*( 0) |
|
2) = χ˜ s2 |
– 1 = χ 22 |
( s – 1) ⁄ 2. (23) |
|
|
|||||
|
|
„‰Â χ˜ 2s – 1 ВТЪ¸ ТОЫ˜‡ИМ‡fl ‚ВОЛ˜ЛМ‡ ЪЛФ‡ ıЛ-Н‚‡‰-‡Ъ, Т‚flБ‡ММ‡fl Т НУПФОВНТМ˚ПЛ ‚ВОЛ˜ЛМ‡ПЛ „‡ЫТТУ‚‡ ЪЛФ‡ Л ‡‚М‡fl ФУОУ‚ЛМВ У·˚˜МУИ ТОЫ˜‡ИМУИ ‚ВОЛ˜ЛМ˚ ıЛ-Н‚‡‰ ‡Ъ УЪ Ы‰‚УВММУ„У ˜ЛТО‡ ТЪВФВМВИ Т‚У·У‰˚.
äÓ Ì‚ÓÈ ÔÓ‰ıÓ‰ ‚ Í‚‡ÌÚÓ‚ÓÈ ÏÂı‡ÌËÍÂ: ÍÓ Ì‚Ó ͂‡ÌÚÓ‚‡ÌËÂ
иУН‡КВП, ˜ЪУ НУ МВ‚‡fl ТЪ‡ЪЛТЪЛ˜ВТН‡fl ПУ- ‰ВО¸ НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ ВТЪ¸ Н‚‡МЪУ‚‡fl ПВı‡- МЛН‡. к‡ТТПУЪ ЛП ‰Оfl ˝ЪУ„У Т‡П˚И У·˚˜М˚И
“¯ÍÓθÌ˚È” ‚ÚÓ ÓÈ Á‡ÍÓÌ ç¸˛ÚÓ̇
d2 |
1 ∂ U |
(24) |
------x = |
–--- -------. |
|
dt2 |
m ∂ x |
|
и В‰ФУОУКЛП, ˜ЪУ ЩЛ„Ы Л Ы˛˘ЛВ ‚ ˝ЪУП Б‡НУМВ ЫТНУ ВМЛВ Л ТЛО‡ ВТЪ¸ МВНУЪУ ˚В Т В‰МЛВ ‚ВОЛ˜Л- М˚. мТ В‰МВМЛВ У·ВТФВ˜Л‚‡ВЪТfl ФУТ В‰ТЪ‚УП ‚‚В- ‰ВМЛfl МВНУЪУ УИ ФОУЪМУТЪЛ ‡ТФ В‰ВОВМЛfl P(x) ТУУЪМУ¯ВМЛВП
d2 |
∫ P( x) xdx |
1 |
∫ P( x) |
∂ U |
(25) |
dt2 |
= –m |
∂ x dx. |
|||
------ |
|
--- |
|
------- |
|
иУЪ В·ЫВП ЪВФВ ¸, ˜ЪУ·˚ ‚‚В‰ВММ‡fl ФОУЪМУТЪ¸‡ТФ В‰ВОВМЛfl ‰УФЫТН‡О‡ НУ МВ‚УВ ‡БОУКВМЛВ, Ъ.В.
P( x) |
= |
|
ψ ( x) |
|
2 , |
(26) |
|
|
|||||
„‰Â |
|
|
|
|
|
|
ψ ( x) |
= c j ( t)ϕ j ( x) . |
(27) |
||||
иЫТЪ¸ Б‡‚ЛТЛПУТЪ¸ НУ˝ЩЩЛˆЛВМЪУ‚ ‡БОУКВМЛfl УЪ ‚ ВПВМЛ УФ В‰ВОflВЪТfl „‡ ПУМЛ˜ВТНЛПЛ ЩЫМНˆЛflПЛ
c j ( t) = c j0 exp ( –iω j t) . |
(28) |
Е‡БЛТМ˚В ЩЫМНˆЛЛ ‡БОУКВМЛfl Л ˜‡ТЪУЪ˚ Б‡ ‡- МВВ МВЛБ‚ВТЪМ˚. аı ТОВ‰ЫВЪ УФ В‰ВОЛЪ¸ Ъ‡НЛП У·-‡БУП, ˜ЪУ·˚ ‚˚ФУОМflОЛТ¸ ЫТ В‰МВММ˚В Ы ‡‚МВМЛfl ‰‚ЛКВМЛfl. иУ‰ТЪ‡‚Оflfl (26)–(28) ‚ (25), ФУОЫ- ˜ЛП
m( ω j – ω k) 2 c j0 ck*0 k x j exp [ –i( ω j – ω k) t] |
= |
|||
= c j0 ck*0 |
∂ U |
j exp [ –i( ω |
j – ω k) t] . |
(29) |
k ------- |
|
|||
|
∂ x |
|
|
|
á‰ÂÒ¸, Í‡Í Ó·˚˜ÌÓ, ÔÓ ÔÓ‚ÚÓ fl˛˘ËÏÒfl Ë̉ÂÍÒ‡Ï j Ë k Ф В‰ФУО‡„‡ВЪТfl ТЫППЛ У‚‡МЛВ. е‡Ъ Л˜М˚В ˝ОВПВМЪ˚ ‚ ‚˚ ‡КВМЛЛ (29) УФ В‰ВОfl˛ЪТfl ЩУ - ПЫО‡ПЛ
k |
|
x |
|
j = |
∫ |
ϕk*( x) xϕ j ( x) dx, |
(30) |
|
|
|
|||||||
|
|
|||||||
∂ U |
|
j = |
∫ϕ |
∂ U |
j ( x) dx. |
(31) |
||
k ------- |
|
k*( x) -------ϕ |
||||||
∂ x |
|
|
|
∂ x |
|
|
||
СОfl ЪУ„У ˜ЪУ·˚ ТУУЪМУ¯ВМЛВ (29) ‚˚ФУОМflОУТ¸ ‚ О˛·УИ ПУПВМЪ ‚ ВПВМЛ ‰Оfl Ф УЛБ‚УО¸М˚ı М‡- ˜‡О¸М˚ı ‡ПФОЛЪЫ‰, ТОВ‰ЫВЪ ФУЪ В·У‚‡Ъ¸ ‚˚ФУОМВМЛfl ‡‚ВМТЪ‚‡ ОВ‚˚ı Л Ф ‡‚˚ı ˜‡ТЪВИ УЪ‰ВО¸МУ ‰Оfl Н‡К‰У„У П‡Ъ Л˜МУ„У ˝ОВПВМЪ‡. иУ˝ЪУПЫ
|
2 |
∂ U |
|
|
m( ω j – ω k) |
k x j = k ------- j . |
(32) |
||
|
||||
|
|
∂ x |
|
иУТОВ‰МВВ ‚˚ ‡КВМЛВ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ П‡- Ъ Л˜МУВ Ы ‡‚МВМЛВ ЙВИБВМ·В „‡ ‰Оfl Н‚‡МЪУ‚УИ ‰ЛМ‡ПЛНЛ ‚ ˝МВ „ВЪЛ˜ВТНУП Ф В‰ТЪ‡‚ОВМЛЛ. Е‡- БЛТМ˚В ЩЫМНˆЛЛ Л ˜‡ТЪУЪ˚, Ы‰У‚ОВЪ‚У fl˛˘ЛВ ТУ-
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004
йТМУ‚М˚В ФУМflЪЛfl НО‡ТТЛ˜ВТНУИ Л Н‚‡МЪУ‚УИ ТЪ‡ЪЛТЪЛНЛ |
743 |
УЪМУ¯ВМЛflП (32), ВТЪ¸ ТЪ‡ˆЛУМ‡ М˚В ТУТЪУflМЛfl Л ˜‡ТЪУЪ˚ Н‚‡МЪУ‚УИ ТЛТЪВП˚ (‚ ТУУЪ‚ВЪТЪ‚ЛЛ Т ˝Н- ‚Л‚‡ОВМЪМУТЪ¸˛ Н‡ ЪЛМ ЙВИБВМ·В „‡ Л т В‰ЛМ„В-‡). СВИТЪ‚ЛЪВО¸МУ, У· ‡БЫВП ‰Л‡„УМ‡О¸МЫ˛ П‡Ъ-ЛˆЫ ЛБ ˜‡ТЪУЪ ω j ТЛТЪВП˚ . к‡ТТП‡Ъ Л‚‡ВП‡fl П‡Ъ-Лˆ‡ ·Ы‰ВЪ ˝ ПЛЪУ‚УИ ‚ ТЛОЫ ЪУ„У, ˜ЪУ ˜‡ТЪУЪ˚ – ‰ВИТЪ‚ЛЪВО¸М˚В ˜ЛТО‡. щЪ‡ П‡Ъ Лˆ‡ ·Ы‰ВЪ Ф В‰- ТЪ‡‚ОВМЛВП МВНУЪУ У„У ˝ ПЛЪУ‚‡ УФВ ‡ЪУ ‡, ТУ·- ТЪ‚ВММ˚В БМ‡˜ВМЛfl НУЪУ У„У ТЫЪ¸ ω j , Ú.Â.
H|j = ω j |j , |
(33) |
„‰В – Ф УЛБ‚УО¸М‡fl НУМТЪ‡МЪ‡, НУЪУ ‡fl ‚ ЛЪУ„В ‰УОКМ‡ ·˚Ъ¸ УЪУК‰ВТЪ‚ОВМ‡ Т ФУТЪУflММУИ иО‡М- Н‡. з‡И‰ВП fl‚М˚И ‚Л‰ ЛТНУПУ„У УФВ ‡ЪУ ‡ H. З ТЛОЫ (33) П‡Ъ Л˜МУВ ТУУЪМУ¯ВМЛВ (32) ПУКМУ ФВ-ВФЛТ‡Ъ¸ ‚ ‚Л‰В УФВ ‡ЪУ МУ„У Ы ‡‚МВМЛfl
[ H[ Hx] ] |
|
2 |
ˆ |
|
= |
---- |
(34) |
||
m |
∂ U, |
„‰Â ∂ˆ = ∂ /∂ x – УФВ ‡ЪУ ‰ЛЩЩВ ВМˆЛ У‚‡МЛfl, [ ] – НУППЫЪ‡ЪУ . кВ¯ВМЛВП УФВ ‡ЪУ МУ„У Ы ‡‚МВМЛfl (34) fl‚ОflВЪТfl „‡ПЛО¸ЪУМЛ‡М ТЛТЪВП˚
|
2 |
|
2 |
|
|
H = – |
------- |
ˆ |
+ U( x) . |
(35) |
|
2m |
∂ |
|
|||
н‡НЛП У· ‡БУП, ВТОЛ ФУЪ В·У‚‡Ъ¸, ˜ЪУ·˚ НУ МВ- ‚‡fl УˆВМН‡ ФОУЪМУТЪЛ Ы‰У‚ОВЪ‚У flО‡ ‚ Т В‰МВП НО‡ТТЛ˜ВТНЛП Ы ‡‚МВМЛflП ‰‚ЛКВМЛfl, ЪУ ·‡БЛТМ˚В ЩЫМНˆЛЛ Л ˜‡ТЪУЪ˚ НУ МВ‚У„У ‡БОУКВМЛfl ЫКВ МВ ПУ„ЫЪ ·˚Ъ¸ Ф УЛБ‚УО¸М˚ПЛ, ‡ ‰УОКМ˚ Ф В‰ТЪ‡‚- ОflЪ¸ ТУ·УИ ТУУЪ‚ВЪТЪ‚ВММУ ТУ·ТЪ‚ВММ˚В ЩЫМНˆЛЛ Л ТУ·ТЪ‚ВММ˚В БМ‡˜ВМЛfl „‡ПЛО¸ЪУМЛ‡М‡ ТЛТЪВП˚.
з‡ УТМУ‚В ФУОЫ˜ВММУ„У ‚˚ ‡КВМЛfl ‰Оfl „‡ПЛО¸- ЪУМЛ‡М‡ ЫКВ МВЪ Ы‰МУ ФУОЫ˜ЛЪ¸ УФВ ‡ЪУ М˚В Ф В‰ТЪ‡‚ОВМЛfl ‰Оfl ‰ Ы„Лı ‰ЛМ‡ПЛ˜ВТНЛı ‚ВОЛ˜ЛМ. з‡Ф ЛПВ , ФУМflЪЛВ ЛПФЫО¸Т‡ ПУКМУ ‚‚ВТЪЛ М‡ УТМУ‚В ТОВ‰Ы˛˘ВИ ОВ„НУ Ф У‚В flВПУИ ˆВФУ˜НЛ ‡- ‚ВМТЪ‚
|
|
|
|
d |
|
|||||||||
|
|
mdt----∫ P( x) xdx = |
|
|||||||||||
= –im( ω |
j – ω |
k) c j0 ck*0 k |
|
x |
|
j exp [ –i( ω |
j – ω k) t] = |
|||||||
|
|
|||||||||||||
|
im |
|
|
|
|
|
|
|
|
|
|
|
|
(36) |
= |
ψ |
|
Hx – xH |
|
|
ψ = ψ |
|
p |
|
ψ |
. |
|||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
----- |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
иВ ‚УВ ЛБ Ф В‰ТЪ‡‚ОВММ˚ı ‡‚ВМТЪ‚ МВФУТ В‰ТЪ- ‚ВММУ ТОВ‰ЫВЪ ЛБ УФ В‰ВОВМЛfl НУ МВ‚УИ УˆВМНЛ ФОУЪМУТЪЛ. и Л ФУОЫ˜ВМЛЛ ‚ЪУ У„У ‡‚ВМТЪ‚‡ ·˚- ОУ Ы˜ЪВМУ Ы ‡‚МВМЛВ (33). з‡НУМВˆ, ФУТОВ‰МВВ ‡- ‚ВМТЪ‚У ТОВ‰ЫВЪ ЛБ УФ В‰ВОВМЛfl ЛПФЫО¸Т‡ (УФВ ‡- ЪУ ЛПФЫО¸Т‡ ‰УОКВМ ·˚Ъ¸ УФ В‰ВОВМ Ъ‡НЛП У·-‡БУП, ˜ЪУ·˚ В„У Т В‰МВВ БМ‡˜ВМЛВ ТУ‚Ф‡‰‡ОУ Т Ф УЛБ‚В‰ВМЛВП П‡ТТ˚ М‡ Т В‰М˛˛ ТНУ УТЪ¸).
аБ ТУУЪМУ¯ВМЛfl (36) Т МВУ·ıУ‰ЛПУТЪ¸˛ ‚˚ЪВ- Н‡ВЪ ТОВ‰Ы˛˘ВВ УФ В‰ВОВМЛВ ЛПФЫО¸Т‡:
p = |
im |
[ Hx] |
= –i |
∂ |
(37) |
|
∂ x. |
||||
ˆ |
----- |
|
|
----- |
|
б‡ПВЪЛП, ˜ЪУ ‚˚ ‡КВМЛfl ‰Оfl УФВ ‡ЪУ У‚ М‡·О˛- ‰‡ВП˚ı ‚ВОЛ˜ЛМ Б‰ВТ¸ МВ ФУТЪЫОЛ Ы˛ЪТfl (Н‡Н ˝ЪУ ‰ВО‡ВЪТfl Ф Л ТЪ‡М‰‡ ЪМУП ЛБОУКВМЛЛ Н‚‡МЪУ‚УИ ПВı‡МЛНЛ), ‡ ‚˚‚У‰flЪТfl Н‡Н МВУ·ıУ‰ЛП˚В ТОВ‰ТЪ- ‚Лfl НУ МВ‚˚ı ТЪ‡ЪЛТЪЛ˜ВТНЛı УˆВМУН.
лУУЪМУ¯ВМЛfl, ТУ„О‡ТМУ НУЪУ ˚П Ы ‡‚МВМЛfl НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ ‚˚ФУОМfl˛ЪТfl ‚ Т В‰МВП Л ‰Оfl Н‚‡МЪУ‚˚ı ТЛТЪВП, М‡Б˚‚‡˛Ъ Ы ‡‚МВМЛflПЛ щ ВМЩВТЪ‡. л‡ПЛı ˝ЪЛı Ы ‡‚МВМЛИ, НУМВ˜МУ, МВ- ‰УТЪ‡ЪУ˜МУ ‰Оfl УФЛТ‡МЛfl Н‚‡МЪУ‚УИ ‰ЛМ‡ПЛНЛ. д‡Н П˚ ‚Л‰ВОЛ ‚˚¯В, ‰УФУОМЛЪВО¸МУВ ЫТОУ‚ЛВ, НУЪУ УВ ФУБ‚УОflВЪ Ф ВУ· ‡БУ‚‡Ъ¸ НО‡ТТЛ˜ВТНЫ˛ ПВı‡МЛНЫ ‚ Н‚‡МЪУ‚Ы˛ (Ъ.В. ЫТОУ‚ЛВ Н‚‡МЪУ‚‡МЛfl), ВТЪ¸ ФУ ТЫ˘ВТЪ‚Ы Ъ В·У‚‡МЛВ НУ МВ‚У„У ı‡ ‡НЪВ-‡ ФОУЪМУТЪЛ.
Ç˚‚Ó‰˚
ëÙÓ ÏÛÎË ÛÂÏ Í ‡ÚÍÓ ÓÒÌÓ‚Ì˚Â ‚˚‚Ó‰˚.
иУЛТН ПМУ„УФ‡ ‡ПВЪ Л˜ВТНУИ ТЪ‡ЪЛТЪЛ˜ВТНУИ ПУ‰ВОЛ, ‰УФЫТН‡˛˘ВИ ЫТЪУИ˜Л‚УВ ‚УТТЪ‡МУ‚ОВМЛВ Ф‡ ‡ПВЪ У‚ М‡ УТМУ‚В М‡·О˛‰‡ВП˚ı ‰‡ММ˚ı (Н‡Н НО‡ТТЛ˜ВТНЛı, Ъ‡Н Л Н‚‡МЪУ‚˚ı), Ф Л‚У‰ЛЪ Н ФУТЪ УВМЛ˛ НУ МВ‚У„У ФУ‰ıУ‰‡ Н ТЪ‡ЪЛТЪЛ˜ВТНУИ УˆВМНВ ТУТЪУflМЛИ. дУ МВ‚‡fl УˆВМН‡ ТУТЪУflМЛИ УТМУ‚‡М‡ М‡ Ф В‰ТЪ‡‚ОВМЛЛ ФОУЪМУТЪЛ ‚В УflЪМУТЪЛ Н‡Н Н‚‡‰ ‡Ъ‡ ПУ‰ЫОfl МВНУЪУ УИ ЩЫМНˆЛЛ (М‡Б˚- ‚‡ВПУИ ФТЛ-ЩЫМНˆЛВИ ФУ ‡М‡ОУ„ЛЛ Т Н‚‡МЪУ‚УИ ПВı‡МЛНУИ). и В‰ОУКВММ˚И ПВЪУ‰ fl‚ОflВЪТfl ˝Щ- ЩВНЪЛ‚М˚П Т В‰ТЪ‚УП В¯ВМЛfl УТМУ‚МУИ Б‡‰‡˜Л ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡М‡ОЛБ‡ ‰‡ММ˚ı – ‚УТТЪ‡МУ‚ОВМЛfl ТУТЪУflМЛfl ТЪ‡ЪЛТЪЛ˜ВТНУ„У ‡МТ‡П·Оfl ФУ ˝НТФВ ЛПВМЪ‡О¸М˚П М‡·О˛‰ВМЛflП.
З‚В‰ВМЛВ ФТЛ-ЩЫМНˆЛЛ ФУБ‚УОflВЪ Ф В‰ТЪ‡‚ЛЪ¸ П‡Ъ ЛˆЫ ЛМЩУ П‡ˆЛЛ оЛ¯В ‡ Л ТЪ‡ЪЛТЪЛ˜ВТНЛВ Т‚УИТЪ‚‡ УˆВМНЛ ‚ВНЪУ ‡ ТУТЪУflМЛfl ‚ Ф УТЪУП ‡М‡ОЛЪЛ˜ВТНУП ‚Л‰В. йТМУ‚М˚В НУМТЪ ЫНˆЛЛ ЪВУ-ЛЛ (‚ВНЪУ ˚ ТУТЪУflМЛИ, П‡Ъ Лˆ˚ ЛМЩУ П‡ˆЛЛ, НУ‚‡ Л‡ˆЛИ Л Ъ.‰.) УН‡Б˚‚‡˛ЪТfl Ф УТЪ˚ПЛ ЫМЛ- ‚В Т‡О¸М˚ПЛ „ВУПВЪ Л˜ВТНЛПЛ У·˙ВНЪ‡ПЛ ‚ „ЛО¸·В ЪУ‚УП Ф УТЪ ‡МТЪ‚В, ЛМ‚‡ Л‡МЪМ˚ПЛ УЪМУТЛЪВО¸МУ ЫМЛЪ‡ М˚ı (У ЪУ„УМ‡О¸М˚ı) Ф ВУ· ‡- БУ‚‡МЛИ.
дУ˝ЩЩЛˆЛВМЪ˚ ‡БОУКВМЛfl ФТЛ-ЩЫМНˆЛЛ ‚ fl‰ ФУ У ЪУМУ ПЛ У‚‡ММУПЫ М‡·У Ы ЩЫМНˆЛИ УˆВМЛ‚‡- ˛ЪТfl ПВЪУ‰УП П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl, ˜ЪУ У·ЫТОУ‚ОЛ‚‡ВЪ УФЪЛП‡О¸М˚В ‡ТЛПФЪУЪЛ˜ВТНЛВ Т‚УИТЪ‚‡ ПВЪУ‰‡ (‡ТЛПФЪУЪЛ˜ВТНЫ˛ МВТПВ˘ВММУТЪ¸ Л ‡ТЛПФЪУЪЛ˜ВТНЫ˛ ˝ЩЩВНЪЛ‚МУТЪ¸). м ‡‚-
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004
744 |
ÅÓ„‰‡ÌÓ‚ |
МВМЛВ Ф ‡‚‰УФУ‰У·Лfl ‚ ПВЪУ‰В НУ МВ‚УИ УˆВМНЛ ФОУЪМУТЪЛ ЛПВВЪ Ф УТЪЫ˛ Н‚‡БЛОЛМВИМЫ˛ ТЪ ЫНЪЫ Ы Л ‰УФЫТН‡ВЪ ФУТЪ УВМЛВ ˝ЩЩВНЪЛ‚МУИ, ·˚ТЪ-У ТıУ‰fl˘ВИТfl ЛЪВ ‡ˆЛУММУИ Ф УˆВ‰Ы ˚ ‚ Б‡‰‡˜‡ı ·УО¸¯УИ ‡БПВ МУТЪЛ.
дУ МВ‚УИ ФУ‰ıУ‰ fl‚ОflВЪТfl ВТЪВТЪ‚ВММ˚П Т В‰- ТЪ‚УП ‰Оfl ‚УТТЪ‡МУ‚ОВМЛfl ТУТЪУflМЛИ Н‚‡МЪУ‚˚ı ТЪ‡ЪЛТЪЛ˜ВТНЛı ‡МТ‡П·ОВИ ФУ ВБЫО¸Ъ‡Ъ‡П ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪУ‚. и ЛМˆЛФ ‰У- ФУОМЛЪВО¸МУТЪЛ ЕУ ‡ ПУКВЪ Ъ ‡НЪУ‚‡Ъ¸Тfl Н‡Н НУМТЪ ЫНЪЛ‚М˚И ТЪ‡ЪЛТЪЛ˜ВТНЛИ Ф ЛМˆЛФ Н‚‡М- ЪУ‚УИ ЪВУ ЛЛ. лУ„О‡ТМУ ˝ЪУПЫ Ф ЛМˆЛФЫ, ЛМЩУ - П‡ˆЛfl, ТУ‰В К‡˘‡flТfl ‚У ‚Б‡ЛПМУ ‰УФУОМЛЪВО¸- М˚ı ТЪ‡ЪЛТЪЛ˜ВТНЛı ‡ТФ В‰ВОВМЛflı, ПУКВЪ ·˚Ъ¸ Т‚В‰ВМ‡ ‚УВ‰ЛМУ ФУТ В‰ТЪ‚УП ‚‚В‰ВМЛfl Л УˆВМНЛ ФТЛ-ЩЫМНˆЛЛ.
дУ МВ‚УВ Ъ В·У‚‡МЛВ ‰Оfl ФОУЪМУТЪЛ ВТЪ¸ ЫТОУ- ‚ЛВ Н‚‡МЪУ‚‡МЛfl ТЛТЪВП˚. 䂇МЪУ‚‡fl ПВı‡МЛН‡ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ НУ МВ‚Ы˛ ТЪ‡ЪЛТЪЛ˜ВТНЫ˛ ПУ‰ВО¸ НО‡ТТЛ˜ВТНУИ ПВı‡МЛНЛ. З ТЫ˘МУТЪЛ ПУКМУ „У‚У ЛЪ¸ У НУ МВ‚УП Ф ЛМˆЛФВ ‚ ТЪ‡ЪЛТЪЛ˜ВТНУП УФЛТ‡МЛЛ ‰ЛМ‡ПЛ˜ВТНЛı ТЛТЪВП. лУ„О‡ТМУ ˝ЪУПЫ Ф ЛМˆЛФЫ, ‰Оfl ЪУ„У ˜ЪУ·˚ ТЪ‡ЪЛТЪЛ˜ВТНУВ УФЛТ‡МЛВ ·˚ОУ ЫТЪУИ˜Л‚˚П, ТОВ‰ЫВЪ ЛТıУ‰ЛЪ¸ ЛБ НУ МВ‚У„У ‡БОУКВМЛfl ‰Оfl ФОУЪМУТЪЛ ‡ТФ В‰В- ОВМЛfl. л ‰ Ы„УИ ТЪУ УМ˚, ‰Оfl ЪУ„У ˜ЪУ·˚ НУ МВ- ‚УВ ‡БОУКВМЛВ ·˚ОУ ТУ„О‡ТУ‚‡МУ Т Б‡НУМ‡ПЛ ПВ- ı‡МЛНЛ (ЛПВВЪТfl ‚ ‚Л‰Ы ТУ„О‡ТУ‚‡МЛВ ‚ Т В‰МВП), ‚ Н‡˜ВТЪ‚В ·‡БЛТМ˚ı ЩЫМНˆЛИ МВУ·ıУ‰ЛПУ ‚˚· ‡Ъ¸ ТУ·ТЪ‚ВММ˚В ЩЫМНˆЛЛ УФВ ‡ЪУ ‡ ˝МВ „ЛЛ („‡- ПЛО¸ЪУМЛ‡М‡), ‡ ‚ Н‡˜ВТЪ‚В ˜‡ТЪУЪ – ТУУЪ‚ВЪТЪ‚Ы- ˛˘ЛВ ТУ·ТЪ‚ВММ˚В БМ‡˜ВМЛfl. й· ‡БМУ „У‚У fl, МВ ТЫ˘ВТЪ‚ЫВЪ МЛН‡НУ„У ‰ Ы„У„У В„ЫОfl МУ„У ТЪ‡ЪЛТЪЛ˜ВТНУ„У ПВЪУ‰‡ Н УПВ НУ МВ‚У„У, Л МВ ТЫ˘ВТЪ- ‚ЫВЪ МЛН‡НУИ ‰ Ы„УИ В„ЫОfl МУИ ТЪ‡ЪЛТЪЛ˜ВТНУИ ПВı‡МЛНЛ Н УПВ Н‚‡МЪУ‚УИ.
и ЛОУКВМЛВ. ЗУТТЪ‡МУ‚ОВМЛВ ТЪ‡ЪЛТЪЛ˜ВТНЛı
ТУТЪУflМЛИ ПВЪУ‰УП П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl
йˆВМН‡ П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl ‰Оfl ‚ВНЪУ ‡ ТУТЪУflМЛfl ТУУЪ‚ВЪТЪ‚ЫВЪ ˝НТЪ ВПЫПЫ ЩЫМНˆЛЛ Ф ‡‚‰УФУ‰У·Лfl. з‡˜МВП Т ‡М‡ОЛБ‡ ‚Б‡- ЛПМУ ‰УФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪУ‚, Ф У‚В‰ВМ- М˚ı ТУУЪ‚ВЪТЪ‚ВММУ ‚ НУУ ‰ЛМ‡ЪМУП Л ЛПФЫО¸Т- МУП Ф В‰ТЪ‡‚ОВМЛflı. оЫМНˆЛ˛ Ф ‡‚‰УФУ‰У·Лfl УФ В‰ВОЛП ТОВ‰Ы˛˘ЛП ‚˚ ‡КВМЛВП:
|
|
n |
|
m |
|
|
|
|
|
|
∏ |
|
c) ∏ |
˜ |
|
|
(è1) |
|
|
|
|
|||||
L( x, p |
c) = |
P( xi |
P( p j |
|
c) . |
|||
|
|
i = 1 |
|
j = 1 |
|
|
|
|
|
˜ |
(pj |c) – ФОУЪМУТЪЛ ‚У ‚Б‡ЛПМУ ‰У- |
||||||
á‰ÂÒ¸ P(xi |c) Ë P |
||||||||
ФУОМЛЪВО¸М˚ı ˝НТФВ ЛПВМЪ‡ı, ТУУЪ‚ВЪТЪ‚Ы˛˘ЛВ У‰МУПЫ Л ЪУПЫ КВ ‚ВНЪУ Ы ТУТЪУflМЛfl c. иУТОВ ОУ-
„‡ ËÙÏË Ó‚‡ÌËfl ‚˚ ‡ÊÂÌËfl (è1) ÔÓÎÛ˜ËÏ ÙÛÌÍˆË˛ ÎÓ„‡ ËÙÏ˘ÂÒÍÓ„Ó Ô ‡‚‰ÓÔÓ‰Ó·Ëfl
n |
|
|
m |
|
|
|
|
ln L = ∑ |
ln P( xi |
|
c) + ∑ |
˜ |
|
c) . |
(è2) |
|
|
||||||
|
ln P( p j |
|
|||||
i = 1 |
|
|
j = 1 |
|
|
|
|
и ЛМˆЛФ П‡НТЛП‡О¸МУ„У Ф ‡‚‰УФУ‰У·Лfl ТУ‚ПВТЪМУ Т ЫТОУ‚ЛВП МУ ПЛ У‚НЛ, У˜В‚Л‰МУ, Ф Л‚У‰ЛЪ Н Б‡‰‡˜В П‡НТЛПЛБ‡ˆЛЛ ТОВ‰Ы˛˘В„У ЩЫМНˆЛУМ‡О‡:
S = |
ln L – λ( ci ci* – 1) , |
(è3) |
|
„‰В λ– ПМУКЛЪВО¸ ㇄ ‡МК‡ Л |
|
||
ln L = ∑n |
ln [ ci c*j ϕ i ( xk)ϕ *j ( xk) ] + |
|
|
k = 1 |
|
(è4) |
|
+ ∑m |
|
|
|
ln [ ci c*j ϕ˜ i ( pl)ϕ˜ *j ( pl) ] . |
|
||
l = 1 |
|
|
|
á‰ÂÒ¸ ϕ˜ i (p) – Ó· ‡Á îÛ ¸Â ÓÚ ÙÛÌ͈ËË ϕ i(x). çÂÓ·- ıÓ‰ËÏÓ ÛÒÎÓ‚Ë ˝ÍÒÚ ÂÏÛχ ∂ S/∂ c*i = 0 Ô Ë‚Ó‰ËÚ Í Û ‡‚ÌÂÌ˲ Ô ‡‚‰ÓÔÓ‰Ó·Ëfl
Rij c j = λci |
i, j = 0, 1, … , s – 1, |
(è5) |
|||||
„‰Â Ï‡Ú Ëˆ‡ R УФ В‰ВОflВЪТfl ЩУ ПЫОУИ |
|
||||||
Rij = ∑ |
n ϕ |
i*( xk)ϕ j ( xk) |
|
||||
|
------------------------------- + |
|
|||||
|
k = 1 |
|
P |
( xk) |
(è6) |
||
|
|
|
|
|
|||
|
m |
˜ |
* |
( pl)ϕ |
˜ |
j ( pl) |
|
|
|
||||||
+ |
∑ |
ϕ |
i |
|
|
||
|
|
˜ |
|
|
|
||
|
-------------------------------. |
|
|||||
|
l = 1 |
|
P( pl) |
|
|||
|
|
|
|
|
|
||
ᇉ‡˜‡ (и5) fl‚ОflВЪТfl ОЛМВИМУИ ФУ ЩУ ПВ. й‰М‡НУ Т‡П‡ П‡Ъ Лˆ‡ Rij Б‡‚ЛТЛЪ УЪ МВЛБ‚ВТЪМ˚ı ФОУЪМУТ-
ÚÂÈ ( ) Ë ˜ ( ). èÓ˝ÚÓÏÛ ‡ÒÒÏ‡Ú Ë‚‡Âχfl Á‡‰‡˜‡
P x P p
ФУ ТЫ˘ВТЪ‚Ы fl‚ОflВЪТfl МВОЛМВИМУИ Л ‰УОКМ‡, ‚УУ·- ˘В „У‚У fl, В¯‡Ъ¸Тfl ПВЪУ‰УП ЛЪВ ‡ˆЛИ. мПМУ-
ʇfl ÎÂ‚Û˛ Ë Ô ‡‚Û˛ ˜‡ÒÚË Û ‡‚ÌÂÌËfl (è5) ̇ c*i Л ТЫППЛ Ыfl ФУ i, ФУОЫ˜ЛП, ˜ЪУ П‡НТЛП‡О¸МУ Ф ‡‚- ‰УФУ‰У·М˚И ‚ВНЪУ ТУТЪУflМЛfl c ‚ТВ„‰‡ УЪ‚В˜‡ВЪ ТУ·ТЪ‚ВММУПЫ БМ‡˜ВМЛ˛ λ= n + m, ‡‚ÌÓÏÛ ÒÛÏ- χ ÌÓÏÛ ˜ËÒÎÛ ËÁÏ ÂÌËÈ.
м ‡‚МВМЛВ Ф ‡‚‰УФУ‰У·Лfl МВЪ Ы‰МУ Ф В‰ТЪ‡- ‚ЛЪ¸ Ъ‡НКВ Л ‚ ТОВ‰Ы˛˘ВИ ˝Н‚Л‚‡ОВМЪМУИ ЩУ ПВ:
йинадД а лиЦднкйлдйиаь ЪУП 96 ‹ 5 2004
