Программирование, вопросы / Лекц / Л_7_ИсслОп

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Дискретное программирование Лекция 7

Общая характеристика дискретных задач. Математические модели

Значительное место в разнообразных отраслях хозяйства занимают задачи математического программирования, на переменные которых наложены условия целочисленности. Условие целочисленности может быть как в линейных, так и нелинейных задачах. Целочисленные задачи являются разделом широкого класса задач дискретного программирования, переменные которых принимают значение из некоторого дискретного (не обязательно целочисленного), заранее обусловленного числового множества.

В задачах дискретного программирования область допустимых решений является невыпуклой и несвязанной. Поэтому отыскивание решения таких задач сталкивается со значительными трудностями, потому что нельзя использовать стандартные приемы, которые связаны с заменой дискретной задачи ее непрерывным аналогом и последующим округлением полученного решения к ближайшему целочисленному. Следовательно, для решения задач дискретного программирования необходимые специальные методы, которые распределяют на две группы: точные и приближенные. К первой группе относятся методы отсечения, метод ветвей и границ, метод последовательного анализа вариантов и другие; ко второй – методы случайного поиска, эвристические методы и т.п.

По структуре математические модели задач дискретного программирования распределяются на такие основные классы: задачи с нераздельностями, экстремальные комбинаторные задачи, задачи на несвязанных и невыпуклых областях, задаче с разрывными целевыми функциями.

К другим задачам из разных отраслей практики, которые описываются математическими моделями задач дискретного программирования можно отнести задачу коммивояжера, задачу о покрытии, задачи размещения и развития и т.п.

Некоторые задачи формально к дискретным не сводятся, поскольку требование целочисленности в явном виде в них отсутствует. Но при целочисленных значениях некоторых исходных данных, они имеют целочисленный оптимальный план. Сюда можно отнести транспортную задачу и ее модификации. Ко второму типу можно отнести задачу с неделимостями (задача о рюкзаке), к третьему – модели с булевыми переменными (задача о назначении, вариантных задачах размещения производственных сил). Модели комбинаторных задач относятся к четвертому типу (задачи о покрытии), которые нашли широкое применение при проектирования логических и вычислительных устройств.

Постановки задач целочисленного программирования ( ЦП )

Пример 1. Задача целочисленного линейного программирования ( ЦЛП ).

Задачей ЦЛП называют следующую задачу оптимизации :

c,x min

Ax b,

x 0, x- целочисленно.

1

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Здесь c,x Rn, A Rn x m, b Rm. Элементы матрицы A и векторов b и c предполагаются целыми. На рис.1 приведен пример двумерной задачи ЦЛП.

X 2

уб ы ван и ец е ле во йф ун кц и и оп ти м ум зад ач и Ц Л П

о птим умзад ач и Л П д о пус тим аяоб лас ть

X 1

Рис.1. Четыре целочисленные точки, ближайшие к оптимуму задачи ЛП, недопустимы. В некоторых приложениях дробные решения недопустимы, например, в приложении, где xj - число самолетов, назначаемых на маршрут j. Задачи ЛП, формулируемые как задачи ЦЛП, как правило, по своей природе не допускают подхода, основанного на округлении. Один из эффектов округления - это потеря допустимости решения ( см.

рис.1).

Пример 2. Задача о контейнерных перевозках (задача о бомбардировщике или задача о рюкзаке).

Одна из наиболее распространенных задач целочисленного программирования

формулируется так. Контейнер имеет m отсеков вместимостью bi, i=1,m единиц для

перевозки n видов продукции, которую можно брать в количестве 0,1,2 ... единиц.

Пусть aij – затраты i-го отсека на перевозку единицы j-й продукции, а сj - полезность единицы j-й продукции. Нужно найти такой план перевозки, который максимизирует общую полезность рейса. Обозначим хj количество единиц j-й продукции, которая загружена в контейнер. Тогда модель задачи принимает вид

при условиях ограничений на вместимость отсеков

и неотрицательности и целочисленности переменных:

Частным случаем задачи (1) – (4) является задача о ранце, в которой любой из заданного набора предметов можно выбрать или нет, то есть для каждого xj, j = 1,n,

допустимыми значениями являются 0 (предмет не выбирается) или 1 (предмет выбирается). Это приводит к тому, что условие (4) задачи (1) – (4) заменяется требованием

Пример 3. Задача о назначении (задача выбора).

2

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Задача о назначении рассмотренная в лекции о транспортных задачах имеет широкое применение, например, при закреплении машин за маршрутами, распределения инструмента для обработки разных марок стали, рабочих или бригад и т.п. В каждом конкретном случае математическая модель задачи может иметь свою специфику. При назначении на должность для некоторых исполнителей могут существовать ограничения. Например, распределение алгоритмов между вычислительными машинами на ВЦ, как правило, не равняется числу машин. При распределении населенных пунктов между ретрансляционными узлами к одному узлу можно подключать несколько пунктов, и тому подобное. Хотя условие целочисленности xij в ограничениях задачи о назначениях в явном виде отсутствует, оно выполняется, потому что задача о назначении является частным случаем транспортной задачи, в алгоритме решения для которой, нет операции деления.

Пример 4. Транспортная задача с фиксированными доплатами.

Пусть имеем m пунктов производства с объемами ai, i=1,m. Нужно установить такие

Коммивояжеру необходимо объехать n городов 1,2,...,n, начиная с города 1, посещая каждый город ровно один раз, по самому короткому маршруту вернуться в город 1.

Равенства (а) выражают тот факт, что в каждую вершину входит ровно одна дуга, а равенства (б) - тот факт, что из каждой вершины выходит ровно одна дуга.

3

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

В действительности, задача (10) описывает задачу о назначении и содержит в своем допустимом множестве маршрутов маршруты, состоящие из нескольких замкнутых циклов. Нужны дополнительные ограничения для исключения подобных решений.

Пример 6. Задача о выборе транспортных средств.

Разные типы самолетов гражданской авиации отличаются один от другого такими основными показателями как грузоподъемность, вместимость, себестоимость рейса.

Выполняя рейс по i-й авиалинии (i=1,m ) каждый самолет j-го типа (j=1,…n) перевезет

определенное количество пассажиров, грузов, почты. За время рейса он тратит определенное количество ресурсов (горюче-смазочных материалов и тому подобное), которые составляют в стоимостном виде себестоимость рейса сіj. Поскольку тарифная уплата за перевозку пассажира или единицы груза не зависит от типа самолета, то прибыль авиакомпании зависит от назначения самолетов на авиалинии. Поэтому оптимальным распределением самолетов по авиалиниям считают такое, при котором общая себестоимость минимальная при выполнении плана перевозок (или прибыль от перевозок максимальна). Обозначив xij искомое количество самолетов j-го типа, которые назначены на i-ю авиалинию, запишем математическую модель задачи

где Rj, vj, uj – количество пассажиров (вместимость самолета), грузов и почты, которые перевозятся самолетами j -го типа; ai, bi, di – количество пассажиров, грузов и почты соответственно, которые нужны перевезти по i-й авиалинии; nj – количество самолетов j-го типа; kj – коэффициент исправности самолета j-го типа, Sij – максимальное количество рейсов, которые может выполнить самолет j-го типа на i-й авиалинии за определенный период.

Для решения задач ЦП существует множество методов решения, некоторые из которых будут рассмотрены. Начнем с методов отсечения для задачи целочисленного линейного программирования ( пример 1 ). Они дают точное решение за конечное число шагов, но чувствительны к ошибкам округления.

5.2 Метод Гомори

Рассмотрим наиболее изученный класс целочисленных линейных задач, в которых все ограничения и функция линейные, но присутствует требование целочисленности переменных. Множеством планов задач является система точек с целочислоенными координатами, которые принадлежат выпуклому многограннику допустимых решений соответствующей нецелочисленной задачи.

4

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Метод отсечения (метод Гомори) реализуется построением дополнительных линейных ограничений-неравенств, которые определяют отсекающую гиперплоскость. Эти дополнительные ограничения должны удовлетворять двум необходимым условиям:

отсечению, которое заключается в том, что этому ограничению не должен удовлетворять оптимальный план соответствующей нецелочисленной задачи;

правильности, которая заключается в том, что дополнительному ограничению должны удовлетворять все целочисленные планы задачи.

Если условие (19) выполняется для всех переменных, то имеем полностью целочисленную задачу, в противном случае – частично целочисленную.

Предварительный шаг заключается в нахождении решения ЗЛП без условия (19). Пусть такое решение найдено и содержится оно в конечной симплекс-таблице, где Х*=(x1*, ... xm*, 0,..., 0) – оптимальный план, в котором x1*,..., xm* – базисные переменные,

а xm+1, , xn – свободные. Если некоторая переменная, например, хl – дробная, то выполняем общий шаг алгоритма. Для l-ой строки симплекс-таблицы запишем дополнительное ограничение

где alj –дробнаячасть числаalj,а {xi}–дробнаячасть числаxi,

которые определяются так: {alj} = alj – [alj], { xl} = xl – [xl],

где символом [x] обозначена целая часть числа x, то есть наибольшее целое число, которое не превышает x. Заметим, что если задача оптимизации представлена в симметрической форме ( ограничения в виде неравенств ), то балансовые переменные не обязаны быть целыми и в (20) не участвуют.

Теорема. Неравенство (20) определяет правильное отсечение Гомори, то есть:

1)оно является линейным;

2)отсекает найденное нецелочисленное решение задачи (16) – (18);

3)не отсекает ни одного целочисленного плана задачи (16) – (19). Доказательство см. Кузнецов А.В. и др., С. 179-181.

Пример 7. Решим задачу ЦЛП методом Гомори:

Z = x1 + x2 max, 6x1 + 5x2 30,

x2 3,

x1 0, x2 0, x1, x2 – целочисленные.

Отбрасывая условие целочисленности переменных, на первом шаге находим решение ЗЛП симплексным методом. Итоговая симплекс-таблица такая:

5

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Оптимальный план, Z x* 112 . Поскольку переменная P1 дробная, то выполним общий шаг алгоритма. Запишем дополнительное ограничение. Для этого находим, что

Выполняя шаг двойственного симплекс-метода (см. Акулич, стр.107), приходим к завершающей таблице 3.

Вметоде Гомори используют двойственный симплекс-метод, поскольку при переходе

кканоническому равенству в дополнительном ограничении (20) коэффициент при

балансовой переменной и правая часть имеют разные знаки. При внесении этой переменный в базис, правая часть становится отрицательной, что недопустимо для обычного симплекс-метода.

6

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Другие точные методы решения задач ЦП

Полный перебор

В случае, когда допустимое множество задачи ЦП конечно, можно применять метод полного перебора вариантов. Например, допустимое множество задачи коммивояжера конечно. В силу ограниченности возможностей вычислительной техники полный перебор вариантов возможен в задачах небольшой размерности.

Число шагов работы алгоритма как функции от размерности называется сложностью алгоритма. Сложность переборного алгоритма велика. Поэтому актуальной является проблема построения алгоритмов небольшой сложности.

К точным алгоритмам решения задач ЦП относятся : -алгоритм отсекающей плоскости ( Гомори ) для задач ЦЛП ; -метод ветвей и границ ( МВГ ) ; -метод динамического программирования.

Метод ветвей и границ.

МВГ основан на идее разумного перебора вариантов задачи ЦП. В методе МВГ строится последовательное разбиение множества допустимых решений на попарно непересекающиеся подмножества, что можно представить в виде дерева подмножеств.

Слово “ветвей” в названии метода относится к процессу разбиения на подмножества. Слово “границ” относится к нижним оценкам значения решения конкретного подмножества. В процессе решения используется также некоторое “рекордное” значение решения, достигнутое либо в процессе работы алгоритма, либо полученное некоторым алгоритмом, которое регулярно пересматривается по мере появления конкретных решений. “Рекордное” значение позволяет отсекать (исключать из решения) подмножества решений с большими значениями нижних границ.

Алгоритм МВГ :

1.Задать SA = S0, т.е. активное множество, равное исходному множеству решений ; Положить рекордное значение u = .

2.До тех пор, пока активное множество не пусто, выполнять действия :

2.1.Выбрать вершину ветвления S SA и удалить S из SA.

2.2.Произвести ветвление, т.е. дробление S на подмножества S1,S2 , ,SnS и

вычислить соответствующие им границы zi (нижние – для задачи минимизации, верхние – для максимизации некой функции качества ).

2.3.Для i 1,2, ,ns выполнить действия :

2.3.1.Если zi u, то { исключить множество Si из рассмотрения } иначе { Если Si - решение, то {u = zi} иначе { добавить Si к активномумножеству SA}}.

Пример 1. ( Задача о кратчайшем пути на орграфе )

Рисунок 1. Задача о кратчайшем пути.

7

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

u1 6- “рекорд”

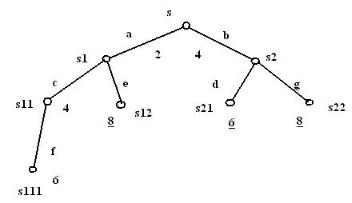
Рисунок 2. Дерево поиска, полученное при условии, что ветвление производится в вершине наименьшей нижней границы.

Рассмотрим задачу о кратчайшем пути в графе с неотрицательными весами 2,4,2,2,6,2,4 дуг a, b, c, d, e, f, g, соответственно (Рис.1). Ветвление в этой задаче - это выбор очередной дуги. В качестве нижней оценки примем суммарную длину частичного пути до некоторой вершины из окружения данной. На Рис.2. приведены шаги ветвления в предположении, что ветвление производится для вершины из активного множества с наименьшей нижней оценкой. Шаги ветвления можно выразить схемой :

на шаге 3 получен первый “рекорд” u1 6. Это позволяет исключить из активного множества вершину дерева -S12.

исключаются вершины S21 и S22.

5. Поскольку в активном множестве нет вершин, процесс закончен.

Пример 2. МВГ для ЦЗ

Процесс начинается с решения исходной задачи без требования целочисленности переменных. Если оптимальный план Х* задачи математического программирования на максимум с выпуклыми ограничениями не удовлетворяет условию целочисленности, то значение целевой функции = Z(X*) дает верхнюю оценку искомого решения (рекорд) на множестве G0 планов задачи. Дробную базисную переменную, например, хl, в целочисленном плане следует либо уменьшить к [хl], либо увеличить до [хl]+1.

8

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Находим решение и оценки на этих подмножествах. Если решение на G1(1) и G1(2)

целочисленные, то оптимальным будет то, в котором оценка более большая. Если же допустим, что для множества G1(1) имеем целочисленное решение, а наG1(2) – дробное, но

(G1(2) ) (G1(1) ), то продолжаем разбивать подмножество, поскольку на следующем шаге можем найти целочисленный план, оценка которого будет превышать оценку (G1(1) ).

Этот процесс длится до тех пор, пока не будут найдены целочисленные решения с максимальной оценкой.

Пример. Решить целочисленную задачу линейного программирования методом ветвей и границ

Z = x1 + 2x2 max, 2x1+ 2x2 7,

4x1- 5x2 9,

x1 0, x2 0,

x1, x2 – целочисленные.

Используя геометрическую интерпретацию. На предварительном шаге, находим решение исходной задачи линейного программирования без условий целочисленности

переменных на множестве планов задачи G0 (рис. 1.а). Верхняя оценка (G0) = 7, а оптимальный план Х* = (0, 7/2). Поскольку переменная х2 дробная, то в целочисленном решении ее следует или уменьшить её до [7/2] = 3, или увеличить до [7/2] + 1 = 4.

Разобьем множество G0 на два подмножества G1(1) иG1(2) , где

Решив две ЗЛП на подмножествах G1(1) и G1(2) (рис. 3.б), найдем

Разобьем подмножество G1(1) на G(1)2 и G(22) (рис. 3.в), где

G(1)2 {X X G1(1) } {x1 0},

G2(2) {X X G1(1) } {x1 1}.

Решая эти ЗЛП, получаем

9

Л_7_ИсслОп.doc = "Дискретное программирование Л1.doc" + "Дискретное программирование Л2.doc"

Получаем

Χ3(1) (32,2), (G3(1)) 112 (G2(1)),

G(32) .

На этом решение целочисленной ЗЛП закончено и можно заключить, что оптимальным решением является

На рис. 3 приведена геометрическая интерпретация решения исходной задачи, а на рис. 4 – дерево решений.

Рисунок 3. – Геометрическая интерпретация решения исходной задачи:

Рисунок 4. – Дерево решений

Пример 3. МВГ для задачи коммивояжера.

10