Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Полшков Ю.Н. Лаб. задания по ТВиМС.pdf

Скачиваний:

Добавлен:

13.04.2015

Размер:

1.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

ЛАБОРАТОРНЫЕ ЗАДАНИЯ

Лабораторная работа № 7 по математической статистике

1) Проведены наблюдения за парой признаков (X ;Y ) . Предполагая, что признаки связаны линейной зависимостью, требуется: а) вычислить выборочный коэффициент корреляции rB и дать ему объяснение; б) найти выборочное уравнение

yx = a +b х

прямой линии регрессии Y на X ; в) построить корреляционное поле и нанести на нем полученную прямую регрессии.

2) Предполагая, что связь между признаками нелинейная, требуется: а) вычислить ηyx –

выборочное корреляционное отношение Y к X и дать ему объяснение; б) найти уравнения криволинейной регрессии

yx = cx2 + dx +e (парабола второго порядка), yx = f ln(x) + g (логарифмический тип), yx = hxk (степенной тип),

yx = lemx (экспоненциальный тип),

yx = n sin(x) + p cos(x) +q sin(2x) + s cos(2x) (тригонометрический многочлен), где c, d, e, f , g, h, k, l, m, n, p, q, s – константы, подлежащие определению; в) выяснить

какая из кривых регрессии точнее сглаживает экспериментальную зависимость и построить эту кривую в корреляционном поле.

Вариант 1

Y			X
Y	5	10	15	20	25
10	1	1	1
25	1	3	1
40			5	1
55			1	2	3
70					3
Вариант 3
Y			X
Y	2	4	6	8	10
2			1	1	3
4		1	5	2
6		1	1
8	1	2	1
10	1
Вариант 5
Y			X
Y	1	3	5	7	9
20	1	1	1
40	1	2	1
60		1	5	1
80			1	2	1
100					2

Вариант 2

Y			X
Y	1	2	3	4	5
3	1	1	1
12	1	2	1
21		1	4	1
30			2	1	2
39				1	1
Вариант 4
Y			X
Y	1	2	3	4	5
2	1	1
3	1	2
4		1			1
5			8	2	1
6				1	1
Вариант 6
Y			X
Y	1	2	3	4	5
8	2	3	1
18		3	1
28		1	6	1
38			1	2	1
48					2

ЛАБОРАТОРНЫЕ ЗАДАНИЯ

Вариант 7

Y			X
Y	1	2	3	4	5
1			1	3	2
3			5	1
5	1	2	1
7	1	1	1
9	1
Вариант 9
Y			X
Y	0	1	2	3	4
9	2	1	1
12	1	1	1
15		1	4
18			1	3
21			1	1	2

Вариант 11

Вариант 8

Y			X
Y	1	2	3	4	5
0			3	3	2
2		2	4	1
4	1	1	1
6	1
8	2
Вариант 10
Y			X
Y	1	2	3	4	5
-3		3			2
-2		3
-1			5	4
0			5	4
1	3		3

X	1	2	3	3	3	3	3	4	4	5
Y	0	1	3	4	3	4	5	9	7	9
Вариант 12
X	1	2	3	3	3	3	3	4	4	5
Y	3	11	21	21	21	21	21	33	33	47
Вариант 13
X	1	2	3	3	3	3	3	4	4	5
Y	9	8,5	7	6	6,5	7	7	6	5	5
Вариант 14
X	1	2	2	3	3	3	3	4	5	5
Y	3	4,39	4,39	5,19	5,21	5,2	5,2	5,77	5,77	6,22
Вариант 15
X	1	2	2	3	3	3	3	4	5	5
Y	0,1	0,08	0,07	0,08	0,07	0,06	0,07	0,06	0,05	0,05
Вариант 16
X	1	2	2	3	3	3	3	4	5	5
Y	6	17	16	31	31,2	31,2	35	50	65	60
Вариант 17
X	1	2	2	2	3	3	4	4	4	5
Y	0,1	0,2	0,19	0,18	0,19	0,3	0,4	0,39	0,5	0,49

ЛАБОРАТОРНЫЕ ЗАДАНИЯ

Вариант 18

X	1	2	2	2	3	3	4	4	4	5
Y	7,36	2,71	2,707	2,71	1	0,99	0,37	0,366	0,37	0,13
Вариант 19
X	1	2	2	2	3	3	4	4	4	5
Y	9	1	1	0,9	-7	-6,5	-13	-14	-15	-20
Вариант 20
X	0	1	2	2	3	3	4	4	4	5
Y	3	2,37	-2,33	-2,32	0,5	0,51	0,27	0,28	0,29	-3,44
Вариант 21
X	1	2	3	3	3	3	3	4	4	5
Y	2	6	11	12	12	12	11	16	17	20
Вариант 22
X	1	2	3	3	3	3	3	4	4	5
Y	-4,5	-11,8	-25	-25,1	-25,1	-25,1	-25,2	-44,4	-44,4	-69,7
Вариант 23
X	1	2	3	3	3	3	3	4	4	5
Y	-9	-20	-29	-30	-31	-29	-29	-40	-39	-48
Вариант 24
X	1	2	2	3	3	3	3	4	5	5
Y	37	25,22	25,22	18,32	18,001	18,32	18,32	13,43	9,6	9,6
Вариант 25
X	1	2	2	3	3	3	3	4	5	5
Y	1	0,8	0,9	0,7	0,8	0,6	0,7	0,5	0,5	0,5
Вариант 26
X	1	2	2	3	3	3	3	4	5	5
Y	-1,6	-2,26	-2,3	-2,77	-2,8	-2,8	-2,8	-3,2	-3,58	-3,6
Вариант 27
X	1	2	2	2	3	3	4	4	4	5
Y	0,2	0,33	0,3	0,32	0,44	0,45	0,6	0,55	0,55	0,7
Вариант 28
X	1	2	2	2	3	3	4	4	4	5
Y	-3	-9	-8	-8,9	-24	-24,1	-65	-65,5	-65	-180
Вариант 29
X	1	2	2	2	3	3	4	4	4	5
Y	-3	-9	-8	-9	-13	-13,4	-18,4	-18,4	-18,4	-23

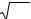
ЛАБОРАТОРНЫЕ ЗАДАНИЯ

Вариант 30

X	0	1	2	2	3	3	4	4	4	5
Y	19	-26,27	0,44	0,43	9,89	9,91	-23,55	-23,6	-23,6	9,64

Приложение 1

	Таблица значений функции Гаусса ϕ(x) =								1		e−x2 / 2
	Таблица значений функции Гаусса ϕ(x) =									2π	e−x2 / 2
										2π
x	ϕ(x)	x	ϕ(x)	x	ϕ(x)	x	ϕ(x)	x		ϕ(x)		x	ϕ(x)
0	0,3989	0,7	0,3123	1,4	0,1497	2,1	0,0440	2,8	0,0079			3,5	0,0009
0,01	0,3989	0,71	0,3101	1,41	0,1476	2,11	0,0431	2,81	0,0077			3,51	0,0008
0,02	0,3989	0,72	0,3079	1,42	0,1456	2,12	0,0422	2,82	0,0075			3,52	0,0008
0,03	0,3988	0,73	0,3056	1,43	0,1435	2,13	0,0413	2,83	0,0073			3,53	0,0008
0,04	0,3986	0,74	0,3034	1,44	0,1415	2,14	0,0404	2,84	0,0071			3,54	0,0008
0,05	0,3984	0,75	0,3011	1,45	0,1394	2,15	0,0396	2,85	0,0069			3,55	0,0007
0,06	0,3982	0,76	0,2989	1,46	0,1374	2,16	0,0387	2,86	0,0067			3,56	0,0007
0,07	0,3980	0,77	0,2966	1,47	0,1354	2,17	0,0379	2,87	0,0065			3,57	0,0007
0,08	0,3977	0,78	0,2943	1,48	0,1334	2,18	0,0371	2,88	0,0063			3,58	0,0007
0,09	0,3973	0,79	0,2920	1,49	0,1315	2,19	0,0363	2,89	0,0061			3,59	0,0006
0,1	0,3970	0,8	0,2897	1,5	0,1295	2,2	0,0355	2,9	0,0060			3,6	0,0006
0,11	0,3965	0,81	0,2874	1,51	0,1276	2,21	0,0347	2,91	0,0058			3,61	0,0006
0,12	0,3961	0,82	0,2850	1,52	0,1257	2,22	0,0339	2,92	0,0056			3,62	0,0006
0,13	0,3956	0,83	0,2827	1,53	0,1238	2,23	0,0332	2,93	0,0055			3,63	0,0005
0,14	0,3951	0,84	0,2803	1,54	0,1219	2,24	0,0325	2,94	0,0053			3,64	0,0005
0,15	0,3945	0,85	0,2780	1,55	0,1200	2,25	0,0317	2,95	0,0051			3,65	0,0005
0,16	0,3939	0,86	0,2756	1,56	0,1182	2,26	0,0310	2,96	0,0050			3,66	0,0005
0,17	0,3932	0,87	0,2732	1,57	0,1163	2,27	0,0303	2,97	0,0048			3,67	0,0005
0,18	0,3925	0,88	0,2709	1,58	0,1145	2,28	0,0297	2,98	0,0047			3,68	0,0005
0,19	0,3918	0,89	0,2685	1,59	0,1127	2,29	0,0290	2,99	0,0046			3,69	0,0004
0,2	0,3910	0,9	0,2661	1,6	0,1109	2,3	0,0283	3	0,0044			3,7	0,0004
0,21	0,3902	0,91	0,2637	1,61	0,1092	2,31	0,0277	3,01	0,0043			3,71	0,0004
0,22	0,3894	0,92	0,2613	1,62	0,1074	2,32	0,0270	3,02	0,0042			3,72	0,0004
0,23	0,3885	0,93	0,2589	1,63	0,1057	2,33	0,0264	3,03	0,0040			3,73	0,0004
0,24	0,3876	0,94	0,2565	1,64	0,1040	2,34	0,0258	3,04	0,0039			3,74	0,0004
0,25	0,3867	0,95	0,2541	1,65	0,1023	2,35	0,0252	3,05	0,0038			3,75	0,0004
0,26	0,3857	0,96	0,2516	1,66	0,1006	2,36	0,0246	3,06	0,0037			3,76	0,0003
0,27	0,3847	0,97	0,2492	1,67	0,0989	2,37	0,0241	3,07	0,0036			3,77	0,0003
0,28	0,3836	0,98	0,2468	1,68	0,0973	2,38	0,0235	3,08	0,0035			3,78	0,0003
0,29	0,3825	0,99	0,2444	1,69	0,0957	2,39	0,0229	3,09	0,0034			3,79	0,0003
0,3	0,3814	1	0,2420	1,7	0,0940	2,4	0,0224	3,1	0,0033			3,8	0,0003
0,31	0,3802	1,01	0,2396	1,71	0,0925	2,41	0,0219	3,11	0,0032			3,81	0,0003
0,32	0,3790	1,02	0,2371	1,72	0,0909	2,42	0,0213	3,12	0,0031			3,82	0,0003
0,33	0,3778	1,03	0,2347	1,73	0,0893	2,43	0,0208	3,13	0,0030			3,83	0,0003
0,34	0,3765	1,04	0,2323	1,74	0,0878	2,44	0,0203	3,14	0,0029			3,84	0,0003
0,35	0,3752	1,05	0,2299	1,75	0,0863	2,45	0,0198	3,15	0,0028			3,85	0,0002
0,36	0,3739	1,06	0,2275	1,76	0,0848	2,46	0,0194	3,16	0,0027			3,86	0,0002
0,37	0,3725	1,07	0,2251	1,77	0,0833	2,47	0,0189	3,17	0,0026			3,87	0,0002
0,38	0,3712	1,08	0,2227	1,78	0,0818	2,48	0,0184	3,18	0,0025			3,88	0,0002
0,39	0,3697	1,09	0,2203	1,79	0,0804	2,49	0,0180	3,19	0,0025			3,89	0,0002
0,4	0,3683	1,1	0,2179	1,8	0,0790	2,5	0,0175	3,2	0,0024			3,9	0,0002
0,41	0,3668	1,11	0,2155	1,81	0,0775	2,51	0,0171	3,21	0,0023			3,91	0,0002

				ЛАБОРАТОРНЫЕ ЗАДАНИЯ							44
			Продолжение приложения 1

x	ϕ(x)	x	ϕ(x)	x	ϕ(x)	x	ϕ(x)	x	ϕ(x)	x	ϕ(x)
0,42	0,3653	1,12	0,2131	1,82	0,0761	2,52	0,0167	3,22	0,0022	3,92	0,0002
0,43	0,3637	1,13	0,2107	1,83	0,0748	2,53	0,0163	3,23	0,0022	3,93	0,0002
0,44	0,3621	1,14	0,2083	1,84	0,0734	2,54	0,0158	3,24	0,0021	3,94	0,0002
0,45	0,3605	1,15	0,2059	1,85	0,0721	2,55	0,0154	3,25	0,0020	3,95	0,0002
0,46	0,3589	1,16	0,2036	1,86	0,0707	2,56	0,0151	3,26	0,0020	3,96	0,0002
0,47	0,3572	1,17	0,2012	1,87	0,0694	2,57	0,0147	3,27	0,0019	3,97	0,0002
0,48	0,3555	1,18	0,1989	1,88	0,0681	2,58	0,0143	3,28	0,0018	3,98	0,0001
0,49	0,3538	1,19	0,1965	1,89	0,0669	2,59	0,0139	3,29	0,0018	3,99	0,0001
0,5	0,3521	1,2	0,1942	1,9	0,0656	2,6	0,0136	3,3	0,0017	4	0,0001
0,51	0,3503	1,21	0,1919	1,91	0,0644	2,61	0,0132	3,31	0,0017	4,01	0,0001
0,52	0,3485	1,22	0,1895	1,92	0,0632	2,62	0,0129	3,32	0,0016	4,02	0,0001
0,53	0,3467	1,23	0,1872	1,93	0,0620	2,63	0,0126	3,33	0,0016	4,03	0,0001
0,54	0,3448	1,24	0,1849	1,94	0,0608	2,64	0,0122	3,34	0,0015	4,04	0,0001
0,55	0,3429	1,25	0,1826	1,95	0,0596	2,65	0,0119	3,35	0,0015	4,05	0,0001
0,56	0,3410	1,26	0,1804	1,96	0,0584	2,66	0,0116	3,36	0,0014	4,06	0,0001
0,57	0,3391	1,27	0,1781	1,97	0,0573	2,67	0,0113	3,37	0,0014	4,07	0,0001
0,58	0,3372	1,28	0,1758	1,98	0,0562	2,68	0,0110	3,38	0,0013	4,08	0,0001
0,59	0,3352	1,29	0,1736	1,99	0,0551	2,69	0,0107	3,39	0,0013	4,09	0,0001
0,6	0,3332	1,3	0,1714	2	0,0540	2,7	0,0104	3,4	0,0012	4,1	0,0001
0,61	0,3312	1,31	0,1691	2,01	0,0529	2,71	0,0101	3,41	0,0012	4,11	0,0001
0,62	0,3292	1,32	0,1669	2,02	0,0519	2,72	0,0099	3,42	0,0012	4,12	0,0001
0,63	0,3271	1,33	0,1647	2,03	0,0508	2,73	0,0096	3,43	0,0011	4,13	0,0001
0,64	0,3251	1,34	0,1626	2,04	0,0498	2,74	0,0093	3,44	0,0011	4,14	0,0001
0,65	0,3230	1,35	0,1604	2,05	0,0488	2,75	0,0091	3,45	0,0010	4,15	0,0001
0,66	0,3209	1,36	0,1582	2,06	0,0478	2,76	0,0088	3,46	0,0010	4,16	0,0001
0,67	0,3187	1,37	0,1561	2,07	0,0468	2,77	0,0086	3,47	0,0010	4,17	0,0001
0,68	0,3166	1,38	0,1539	2,08	0,0459	2,78	0,0084	3,48	0,0009	4,18	0,0001
0,69	0,3144	1,39	0,1518	2,09	0,0449	2,79	0,0081	3,49	0,0009	4,19	0,0001

Например, требуется определить ординату функции Гаусса в точке x =1,33

(рис. 1). Имеем (в табл. приложения 1 выделено жирным шрифтом):

ϕ(1,33) = 0,1647 .

Напомним, что функция Гаусса – четная, т.е.

ϕ(−x) = ϕ(x) .

Кроме того,

ϕ(x) = N(0,1) ,

т.е. является плотностью нормированного нормального распределения.

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.04.2019723.46 Кб12Полонский П. Введение в философию иудаизма.doc
#
08.08.2019480.77 Кб11Полшков Ю.Н. Задания по ОММ.doc
#
13.04.2015443.34 Кб13Полшков Ю.Н. Задания по ОММ.pdf
#
29.04.20194.79 Mб23Полшков Ю.Н. Курс лекций по ОММ.doc
#
13.04.20154.63 Mб173Полшков Ю.Н. Курс лекций по ТВиМС.pdf
#
13.04.20151.17 Mб59Полшков Ю.Н. Лаб. задания по ТВиМС.pdf
#
06.09.201932 Кб1полытолог 28.04.docx
#
08.05.2019343.04 Кб6Пользовательский интерфейс Access 2010_1.doc
#
01.04.2025342.02 Кб0Поляков Ю.А. Информационная безопасность и сред...doc
#
13.04.2015235.21 Кб11Поляков Юрий. Апофегей - royallib.ru.doc
#
13.04.20151.81 Mб7пономарев.rtf