
Мет.атом
.pdf31
Решение. Примером потенциальной функции, сферически-симметричной относительно некоторого силового центра, может служить положительно заряженное атомное ядро, в электрическом поле которого движется электрон. В этом случае решение уравнения Шредингера (3.5) удобно находить в сферических координатах.
Оператор Лапласа в сферических координатах имеет вид:
|
2 |
|
1 |
2 |
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
. |
|
r2 |
|
|
|
|
|
|
r2 sin2 |
2 |
|||||||||||||
|
|
|
|
r |
|
r |
|
r2 sin |
|
|
|
|||||||||||
Так как по условию задачи не зависит от угловых переменных, то в операторе Лапласа отличным от нуля остаётся только первое слагаемое, и уравнение Шредингера для стационарных состояний запишется в виде:
d2 |
|
2 d |
|
2m |
(E U) 0. |
|||
|
|
|
|
|
||||
dr2 |
r dr |
2 |
||||||
|
|
|
||||||
Используя замену (r) /r , это уравнение можно привести к виду:
d2 |
|
2m |
(E U) 0 |
|
dr2 |
2 |
|||
|
|
Полученное уравнение математически тождественно с уравнением Шредингера для одномерной потенциальной ямы конечной глубины - U0 (3.8). Поэтому результаты, полученные в задаче 8, сохраняют силу для вспомогательной функции (r).
Найдём решение для двух областей.
|
|
|
d2 |
|
|
|
|
k2 |
|
где k2 |
|
|
2mE |
|
|
|
|
|
I) |
r < r0, |
U(r) = 0, |
|
1 |
|
|
0 |
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dr2 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d2 |
|
2 |
|
|
2 2 |
0 |
, где 2 |
|
2m(U |
0 |
E) |
||||
II) |
r > r0, |
U(r) = U0, |
|
|
|
|
|
|
|
|
|
. |
||||||
dx2 |
|
2 |
|
|||||||||||||||
|
Общие решения этих уравнений |
|
|
|
|
2(r) Be r Ce r |
|
|
|
|
|
|||||||
|
|
1(r) Asin(kr ) |
|
|
|
|
|
|||||||||||
должны удовлетворять стандартным условиям.
При r = 0 функция должна быть равна нулю, иначе (r) /r в этой точке будет обращаться в . Чтобы -функция всюду оставалась конечной, необходимо соблюдение условия 0, следовательно при r < r0
1(r) Asin(kr).
В силу ограниченности во всём пространстве необходимо потребовать, чтобы при r 0, следовательно при r > r0 В = 0 и
|
|
|
|
2(r) Ce r . |
||
|
Для -функции тогда имеем: |
|||||
I) |
0 r < r0, |
(r) A |
sin(kr) |
. |
||
|
|
|||||
|
|
1 |
|
r |
||
|
|
|
|
|||
|
|
2(r) |
Ce r |
|||
II) |
r > r0, |
|
. |
|
||
|
|
|||||
|
|
|
|
r |
||

32
На границе областей при r = r0 из условий непрерывности волновой функции и её производной по координате следует:
1(r0) 2(r0),
1 (r0) 2 (r0).
Отсюда
tg(kr0) k ,
следовательно
sinkr0 kr0 
 2 /2mr02U0 .
2 /2mr02U0 .
Задача 10. Используя формулу для коэффициента прозрачности потенциального барьера (3.8), найти вероятность прохождения частицы с массой m и энергией Е сквозь потенциальный барьер (рис. 3.7), где
U |
|
U(x) U0(1 x2 /l2). |
|
|
|
||
|
U0 |
Решение. По классическим представлениям, |
|||||
|
частица, |
встретившая |
на |
своём |
пути |
||
|
|
||||||
|
|
потенциальный |
барьер |
высоты |
U0, |
||
|
|
беспрепятственно пройдёт над барьером, если её |
|||||
|
|
энергия Е > U0, если же Е < U0, то частица |
|||||
|
|
отразится |
от |
барьера и |
повернёт в обратную |
||
|
|
||||||
Eсторону.
Вквантовой механике поведение частицы
|
|
|
|
|
|
|
|
|
|
|
|
|
выглядит совсем иначе. Во-первых, даже при Е > |
|
|||||||||||||||||||||||||||||||||
|
-l |
0 |
|
|
|
l |
|
x |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
U0 |
отлична от нуля вероятность того, |
что частица |
|
|||||||||||||||||||||||||||||||||||||
|
Рис. 3.7 |
|
|
|
|
|
отразится |
от |
|
барьера |
|
|
и |
|
повернёт |
в обратную |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
сторону, во вторых, при |
Е < |
U0 |
отлична от нуля |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
вероятность того, что частица пройдёт сквозь барьер. Эту способность |
|
||||||||||||||||||||||||||||||||||||||||||||||
квантовой частицы проходить сквозь барьер как бы по туннелю, называют |
|
||||||||||||||||||||||||||||||||||||||||||||||
туннельным эффектом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Вероятность прохождения частицы сквозь барьер определяется |
|
|||||||||||||||||||||||||||||||||||||||||||||
коэффициентом прозрачности (3.8). Подставляя U(x), получим: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
D exp |
|
2m(U |
0(1 x |
|
/l |
|
) E)dx . |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь x1 |
и x2 |
- координаты точек, между которыми U E (рис. 3.7), поэтому |
|
||||||||||||||||||||||||||||||||||||||||||||
пределы интегрирования найдём из условия: U(x) = E: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x1 l |
|
|
, |
|
|
|
x2 l |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 E/U0 |
|
1 E/U0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Проведя преобразования, для D получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x2 |
|
|
|||||||||||||
2mU0 |
|
|
|
|
|
|
|
2mU0 |
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D exp |
l |
|
|
(x1 |
|
)dx exp |
|
|
l |
|
|
|
|
x |
|
x1 x |
|
|
|
x1 |
arcsin x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
Подставляя пределы интегрирования, получим:

33
|
l |
|
2m |
|
D exp |
|
|
|
(U0 E) . |
|
|
U0 |
||
|
|
|
Задачи для самостоятельного решения.
3.1. Найти длину волны де Бройля для электрона, обладающего кинетической энергией: а) Т = 100 эВ, б) Т = 3 МэВ.
Ответ: а) 2 /
 2mT 1,23 Ǻ,
2mT 1,23 Ǻ,
б) |
|
|
2 |
|
|
0,62 Ǻ. |
|
|
|
|
|||
|
|
|
2mT(1 T /2mc2) |
|||
3.2. Найти |
дебройлевскую |
длину волны молекул водорода, |
||||
соответствующую их наиболее вероятной скорости при комнатной температуре.
Ответ: 2 /
 2mkT 128пм.
2mkT 128пм.
3.3. Какую энергию Е необходимо сообщить нерелятивистскому электрону, чтобы его дебройлевская длина волны уменьшилась в n раз?
Ответ: E 2 2 2 (n2 1), где m-масса электрона. m 2
3.4. При каком значении кинетической энергии дебройлевская длина волны релятивистского электрона равняется его комптоновской длине волны
с?
Ответ: T (
 2 1)mc2 0,21МэВ.
2 1)mc2 0,21МэВ.
3.5.Найти длину волны де Бройля для протонов, если в однородном магнитном поле с индукцией В радиус кривизны их траектории - окружности – равен R.
Ответ: 2 /eBR.
3.6.При каком значении скорости v дебройлевская длина волны релятивистского электрона равняется его комптоновской длине волны с?
Ответ: v c/
 2 2,12 108 м/с.
2 2,12 108 м/с.
3.7. Найти кинетическую энергию электронов, падающих нормально на диафрагму с двумя узкими щелями, если на экране, отстоящем от диафрагмы на расстоянии l = 75 см, расстояние между соседними максимумами х = 7,5 мкм. Расстояние между щелями d = 25 мкм.
Ответ: T 2( l/d x)2 /m 24эВ.
3.8. Параллельный пучок моноэнергетических электронов, падает нормально на диафрагму с узкой прямоугольной щелью ширины b = 1 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние l = 50 см, ширина центрального дифракционного максимума
x 0,36 мм.

34
Ответ: v 4 l 2 106 м/с . mb x
3.9. Параллельный пучок нерелятивистских электронов, ускоренных разностью потенциалов U = 25 В, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Определить расстояние между соседними максимумами дифракционной картины на экране, отстоящем от диафрагмы на расстояние l =100 см.
Ответ: x |
|
2 l |
|
4,9 мкм. |
|
|
|
|
|
||
d |
|
2meU |
|||
|
|
|
|
||
3.10. Узкий пучок моноэнергетических электронов падает под углом скольжения =30° на естественную грань монокристалла алюминия. Расстояние между соседними кристаллическими плоскостями, параллельными этой грани монокристалла, d = 0,20 нм. При некотором ускоряющем напряжении U0 наблюдали максимум зеркального отражения. Найти U0, если известно, что следующий максимум зеркального отражения возникал при увеличении ускоряющего напряжения U0 в = 2,25 раза.
2 2
Ответ: U0 2me(
 1)2 d2 sin2 0,15кэВ.
1)2 d2 sin2 0,15кэВ.
3.11. Узкий пучок моноэнергетических нерелятивистских электронов с кинетической энергией Т = 180 эВ падает нормально на поверхность монокристалла никеля. В направлении, составляющем угол 55 с направлением падающего пучка, наблюдается максимум отражения четвёртого порядка. Вычислить соответствующее значение межплоскостного расстояния d. Преломления волн не учитывать.
|
|
k |
|
||
Ответ: d |
|
|
|
0,21 |
нм, где k 4. |
|
|
|
|||
|
|
2mT cos( /2) |
|
||
3.12. Пучок электронов, ускоренных разностью потенциалов U = 150 В, падает на поверхность никеля, внутренний потенциал которого Ui = 15 В. Вычислить отношение U/Ui, при котором показатель преломления отличается от единицы не более чем на 1%.
1 Ответ: U /Ui (2 ) 50.
3.13. Оценить неопределенность скорости электрона в атоме водорода, полагая, что размер атома имеет величину порядка l = 0,1 нм. Сравнить полученное значение со скоростью электрона на первой боровской орбите.
Ответ: v /ml 1 106 м/с, |
v 2,2 106 |
м/с. |
|
1 |
|
3.14. Оценить наименьшие ошибки, с которыми можно определить скорость электрона и скорость шарика массы 1 мг, если координаты электрона и центра шарика установлены с неопределенностью 1 мкм.
Ответ: для электрона v 1 104 см/с; для шарика v 1 10 20 см/с.
3.15. Прямолинейная траектория частицы в камере Вильсона представляет собой цепочку малых капелек тумана, размер которых d ≈ 1 мкм.

35
Можно ли, наблюдая след электрона с кинетической энергией Т = 1 кэВ, обнаружить отклонение в его движении от классических законов?
Ответ: угловой разброс импульсов py / p h/ |
2md2T 1,3 угл.с. |
Малость этой величины не позволяет обнаружить указанные ошибки.
3.16.Показать, что для частицы, неопределённость местоположения которой x /2 , где - её дебройлевская длина волны, неопределённость скорости равна самой скорости.
3.17.Оценить с помощью соотношения неопределённостей минимальную кинетическую энергию Т электрона, локализованного в области размером l = 0,2 нм.
Ответ: Tмин 2 /2ml2 1эВ. Здесь взято p p и x l .
3.18. Электрон с кинетической энергией Т 4 эВ локализован в области размером l = 1 мкм. Оценить с помощью соотношения неопределённости относительную неопределённость его скорости.
|
|
|
4. |
||
Ответ: v/v |
|
|
|
1 10 |
|
l |
|
|
|||
|
2mT |
|
|||
3.19. Частица массы m локализована в области размером l. Оценить кинетическую энергию Т частицы, при которой её относительная неопределенность будет порядка 0,01.
Ответ: T 8 104 2 /ml2 . Здесь x l/2.
3.20. Ускоряющее напряжение на электронно-лучевой трубке U ≈ 10 кВ. Расстояние от электронной пушки до экрана l ≈ 20 см. Оценить неопределенность координаты электрона на экране, если след электронного пучка на экране имеет диаметр d ≈ 0,5 мм.
l
Ответ: x  8нм. d
8нм. d 2meU
2meU
3.21. Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками (рис.3.2). Вычислить наименьшую разность двух соседних энергетических уровней (в эВ) электрона,
если l = 10 Å.
3 2 2
Ответ: E 2ml2 1,1эВ.
3.22. Частица массы m движется в одномерном потенциальном поле U kx2 /2 (гармонический осциллятор). Оценить с помощью соотношения неопределённости минимально возможную энергию частицы в таком поле.
Ответ: Емин 
 k/m `, где
k/m `, где 
 k/m - круговая частота осциллятора. Здесь учтено, что p p / x / x, Е = T + U.
k/m - круговая частота осциллятора. Здесь учтено, что p p / x / x, Е = T + U.
3.23. Электрон находится в одномерной прямоугольной потенциальной яме ширины l = 2,5 нм с бесконечно высокими стенками (рис. 3.2). Какую энергию ему надо сообщить, чтобы перевести со второго на третий энергетический уровень?

|
|
|
|
36 |
|
2 |
2(n2 |
n2) |
|
Ответ: E |
|
2 |
1 |
0,3эВ. |
|
2ml2 |
|||
|
|
|
||
3.24. Частица |
находится |
в основном состоянии в одномерной |
||
прямоугольной потенциальной яме ширины l с абсолютно непроницаемыми стенками(0 x l). Найти вероятность пребывания частицы в области
(l/3 x 2l/3).
Ответ: P 1/3 |
3/2 0,61. |
3.25. Частица массы m находится в основном состоянии в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками (рис. 3.2). Максимальное значение плотности вероятности местонахождения частицы равняется Рm. Найти ширину l ямы и энергию Е частицы в данном состоянии.
|
2 |
|
|
( P )2 |
|
Ответ: l |
|
, |
E |
m |
. |
|
|
||||
Pm 8m
3.26. Частица массы m находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками (рис. 3.2). Найти работу, которую необходимо осуществить, чтобы медленно сжать яму в раз.
Ответ: A |
( 2 |
1) 2 2 |
. |
|
2ml2 |
||
|
|
|
3.27. Частица массы m находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками (рис. 3.2). Найти силу давления, которую оказывает частица на стенку.
2 2
Ответ: F ml3 .
3.28. Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы l. Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчёта координаты х в середине ямы.
Ответ: (x) |
2 |
|
cos( |
nx |
), |
если |
(n 1, 3,5,...) |
||||
l |
|
|
|||||||||
|
|
|
|
|
l |
|
|
||||
|
|
|
|
sin( |
nx |
), |
|
|
|||
(x) |
|
2 |
|
если |
(n 2, 4, 6,...) |
||||||
|
|
|
|||||||||
|
|
l |
|
|
|
|
l |
|
|
||
3.29. Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками (рис. 3.2). Найти массу частицы, если ширина ямы l и разность энергий 3-го и 2-го уровней равна Е .
5 2 2
Ответ: m 2l2 E .
3.30. ) Частица массы m находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины l с бесконечно высокими стенками (рис. 3.2). Найти число dN энергетических уровней в интервале энергий (Е, Е+dЕ), если уровни расположены весьма густо.

37
Ответ: dN |
l |
|
m |
dE. |
|
|
|||
|
|
2E |
||
3.31. Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками (рис. 3.2). Найти квантовое число n энергетического уровня частицы, если интервалы энергии до соседних с ним уровней (верхнего и нижнего) относятся как : 1, где = 1,4.
Ответ: n |
1 |
3. |
|
2( 1)
3.32. Волновая функция частицы массы m для основного состояния в одномерном потенциальном поле U(х) kx2 /2 имеет вид:
(x) Aexp( x2), где A и - некоторые постоянные. Найти с помощью уравнения Шредингера постоянную и энергию Е частицы в этом состоянии.
Ответ: |
m |
, |
E |
|
, |
где |
k |
. |
2 |
|
|
||||||
|
|
2 |
|
|
m |
|||
3.33. Определить энергию электрона атома водорода в основном состоянии, для которого волновая функция имеет вид:
(r) A1 ar exp( r), где A и - некоторые постоянные.
k2me2
Ответ:E 8 2 , т. е. уровень с главным квантовым числом n = 2; k 1/4 0 (СИ) .
38
4. Электронная оболочка атома. Спектры.
Основные формулы.
Стационарное уравнение Шредингера в сферической системе координат для сферически симметричного потенциального поля:
d2 |
|
2 d |
|
2m |
(E U) 0 |
(4.1) |
|||
|
|
|
|
|
|||||
dr2 |
r dr |
2 |
|||||||
|
|
|
|
||||||
Собственные значения энергии электрона в водородоподобном атоме:
|
m (kZe2)2 |
|
|
||
Еn |
|
e |
. |
(4.2) |
|
2 2n2 |
|||||
|
|
|
|
||
Здесь Z – заряд ядра, k 1/4 0 , n – главное квантовое число (n = 1, 2, 3, …). Орбитальный момент импульса ML электрона и его проекция Mlz на
заданное направление z:
Ml |
l(l 1), |
(4.3) |
Mlz |
m |
(4.4) |
где l – орбитальное квантовое число (l = 0, 1, 2,…, n-1), m – магнитное квантовое число. При заданном l число m принимает 2l+1 значение:
m = 0, ±1, ±2, …, ±l.
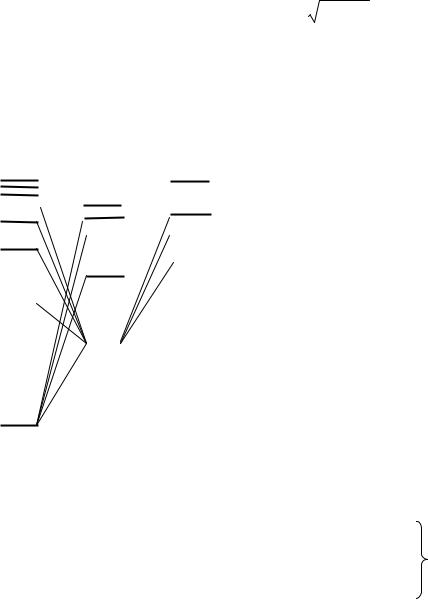
Термы атомов щелочных металлов:
|
S |
|
|
P |
|
|
|
D |
||||||
|
|
|
|
|
|
|
|
|
|
|
S |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
||||
4 |
|
|
|
|
||||||||||
|
|
3 |
|
3 |
|
|
||||||||
|
|
|
|
|
|
|||||||||
3 |
|
|
|
Диффуз- |
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
ная серия |
||||||
Резкая |
2 |
|||||||||||||
|
|
|
|
|
|
|
||||||||
серия |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Главная |
|
|
|
|
Li |
|||||
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
серия |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Рис. 4.1
|
|
En |
|
Z |
2 |
|
|
|
|
Тnl |
|
|
R |
|
, |
(4.5) |
|||
hc |
(n l)2 |
||||||||
|
|
|
|
|
|||||
где Z - заряд "эффективного ядра" (Z = 1 для атомов щелочных металлов и Z ≠ 1 для сходных с ними ионов), l - ридберговская поправка, зависящая от l(или квантовый дефект).
На рис. 4.1 показана схема термов атома лития.
Правило отбора для спектральных серий щелочных металлов:
l 1. |
(4.6) |
Спектральные |
серии щелочных |
металлов в символической форме:
главная серия: |
* ns mp, |
m = n, n+1, n+2, … |
первая побочная (диффузная) серия: |
* np md |
|
вторая побочная (резкая) серия: |
* np ms |
m = n+1, n+2, … (4.7) |
серия Бергмана (фундаментальная) |
* nd mf |
|

39
В явном виде серии записывают как разность двух соответствующих термов. Например, для главной серии лития:
* Т |
2s |
T |
|
R |
|
R |
. |
(4.8) |
|
(2 s)2 |
(n p)2 |
||||||||
|
np |
|
|
|
|
Спиновый момент импульса Ms электрона и его проекция Msz на заданное направление z:
Ms |
|
s(s 1), |
(4.9) |
|
Msz |
ms |
(4.10) |
||
Здесь s –спиновое квантовое число. Для электрона s = 1/2, ms = ±s = ±1/2. |
||||
Полный момент импульса M j электрона и его проекция M jz |
на заданное |
|||
направление z: |
|
|
|
|
M j |
|
|
, |
(4.11) |
j( j 1) |
||||
M jz mj |
(4.12) |
|||
где j – квантовое число полного момента импульса электрона (j = l ±s =l ±1/2). При заданном j возможны 2j+1 квантовых состояний, отличающихся значениями mj:
mj = 0, ±1, ±2, …, ±j.
Для квантового числа j действует правило отбора, согласно которому возможны только те переходы между уровнями, при которых
j 0, 1. |
(4.13) |
|||
Результирующие орбитальный ML |
и спиновый MS |
моменты импульса |
||
многоэлектронного атома: |
|
|
|
|
ML |
|
, |
(4.14) |
|
L(L 1) |
||||
MS |
|
, |
(4.15) |
|
S(S 1) |
||||
где L – квантовое число результирующего орбитального момента, S – квантовое число результирующего cпинового момента.
В случае нормальной спин-орбитальной связи, или связи РассельСаундерса орбитальные моменты электронов складываются в результирующий
орбитальный момент ML, |
а спиновые - |
в результирующий спиновый момент |
||||
MS : |
|
|
|
|
|
|
ML MLi , |
|
|
MS MSi . |
(4.16) |
||
|
i |
|
|
|
i |
|
Взаимодействие ML |
и MS определяет полный механический момент |
|||||
атома: |
MJ |
ML MS |
(4.17) |
|||
|
||||||
|
MJ |
|
|
|
, |
(4.18) |
|
|
J(J 1) |
||||
где J – квантовое число полного момента импульса атома. Оно может принимать одно из следующих значений:

|
|
|
|
|
|
|
|
|
|
|
|
40 |
J |
|
L S |
|
, |
|
L S 1, ..., |
|
L S |
|
. |
|
|
|
|
|
|
|
|
|||||||
Правила отбора для многоэлектронных атомов: |
|
|||||||||||
|
|
|
|
|
|
|
L 0, 1, |
|
||||
|
|
|
|
|
|
|
S 0, |
(4.19) |
||||
|
|
|
|
|
|
|
J 0, 1. |
|
||||
При этом, однако, переход J 0 |
|
|
J 0 запрещён. |
|
||||||||
Правила Хунда для электронов, находящихся в одной подоболочке ( с одинаковыми n и l):
1) Минимальной энергией при данной электронной конфигурации обладает терм с наибольшим возможным значением S и максимально возможным при этом S значении L;
N
М
L
L-cерия
K
K
K
К К-серия
Рис. 4.2
К-серии |
Возбуждение L-серии |
Возбуждение |
|
n
4
3
2
1
2) для основного (нормального) терма
J |
L S |
, |
если |
подоболочка |
|
заполнена |
||||||||
менее чем |
наполовину, и J |
|
L S |
|
в |
|||||||||
|
|
|||||||||||||
остальных случаях. |
|
|
|
|
|
|
|
|
|
|
||||
|
Частоты характеристического |
рентге- |
||||||||||||
новского излучения определяются |
законом |
|||||||||||||
Мозли (рис.4.2): |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
||
|
|
R |
|
|
|
(Z ) |
|
, |
|
|
(4.20) |
|||
|
|
|
n2 |
|
|
|
||||||||
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
i |
|
k |
|
|
|
|
|
|
|
|
|
где Z – порядковый номер элемента, - постоянная экранирования, сильно зависящая от серии (числа ni) и слабо – от линии данной серии (числа nk).
Для K -линий закон Мозли имеет вид:
K |
|
|
3 |
R(Z )2, |
(4.21) |
|
|
||||
|
|
4 |
|
|
|
где = 1 для лёгких атомов.
Методические указания.
п. 4.1. Для щелочных металлов число n в каждой серии постоянное. Ридберговские поправки l в пределах каждой серии остаются практически неизменными, но изменяются от серии к серии.
п. 4.2. Спектральная линия главной серии является самой интенсивной. Эту линию называют резонансной. Для главной серии щелочных металлов один из комбинующихся термов (начальный для поглощения и конечный для испускания) соответствует нормальному, т. е. невозбуждённому состоянию. Для щелочных металлов нормальное состояние принадлежит к s-состояниям. Главное квантовое число для разных щелочных металлов разное:
элемент: Li Na K Rb Cs
