Метода_ТУ

Тема 4 Импеданс динамической системы

Тема 4 Импеданс динамической системы

Анализ различных элементов динамических систем показывает, что разнообразные элементы, отличающиеся назначением, конструкцией, принципом действия и физическими процессами, описываются подобными уравнениями и являются сходными по динамическим свойствам. Рассмотрим понятие импеданса системы как величины, применяющейся для исследования ее динамических свойств.

Электрические системы

На рис. 4.1 представлены схемы простейших электрических систем: активное сопротивление (резистор), индуктивность (катушка индуктивности),

Z (p) = U (p ) , где U (p ) = L[u(t )], I (p) = L[i(t )]. I (p )

Рассмотрим нахождение импеданса представленных электрических систем в соответствии с законами электродинамики.

Как известно из курса физики, система «сопротивление» (рис. 4.1, а)

U (t ) = L di (t ), тогда, при нулевых начальных условиях (н. у.), U (p) = LpI (p). dt

20

Тема 4 Импеданс динамической системы

Импеданс индуктивности (операторное сопротивление индуктивности) равен:

тогда U (p) = 1 I (p ). Импеданс емкости (операторное сопротивление емкости)

Cp

равен:

Механические системы перемещения

На рис. 4.2 представлены схемы простейших механических систем

v(t ) – скорость перемещения, a(t ) – ускорение перемещения, m – масса тела, B – коэффициент демпфирования, k – коэффициент упругости пружины. Будем обозначать преобразования Лапласа указанных функций F (p) = L[ f (t )],

= L[x(t )], V (p) = L[v(t )] и так далее по аналогии.

Для механической системы «масса» (рис. 4.2 а)) в силу второго закона

21

Тема 4 Импеданс динамической системы

Между механическими и электрическими системами существует аналогия, определяемая таблицей 4.1.

Таблица 4.1 – Таблица импедансов различных систем

На основании законов распределения напряжений в цепи при параллельном и последовательном соединениях элементов можно показать, что для электрических сетей при последовательном соединении импедансы

22

Тема 4 Импеданс динамической системы

( Z – импеданс системы, Z1 , …, Zn – импедансы составляющих ее элементов). Кроме того, при решении задач используют законы Кирхгофа:

1)сумма токов (или операторных токов) в каком-либо узле электрической цепи равна нулю;

2)сумма падений напряжений (или операторных напряжений) вдоль любого замкнутого контура равна нулю.

Для решения задачи нахождения выходной величины тока для динамической системы электрической цепи, в которой в качестве входной переменной рассматривается напряжение, необходимо найти импеданс этой цепи (подробнее этот вопрос будет рассмотрен в темах 5 и 6). Для механических систем применяется аналогичный подход (входной переменной является прилагаемая сила, выходной – перемещение или скорость).

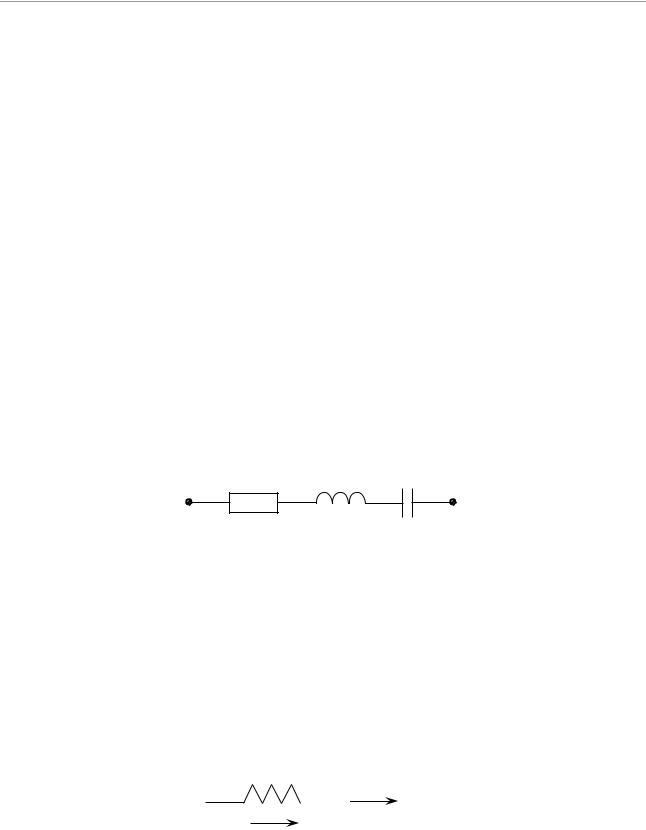
Пример 4.1. Найти импеданс электрической системы (рис. 4.3).

R L C

Рис. 4.3 – Схема динамической системы для примера 4.1

Решение. В данной системе присутствуют 3 элемента (резистор, катушка индуктивности, конденсатор), соединенные последовательно, значит, импеданс системы равен:

Пример 4.2. Найти импеданс механической системы (рис. 4.4).

k

x(t ), v(t )

Рис. 4.4 – Схема динамической системы для примера 4.2

Решение. В данной системе присутствуют 2 элемента (пружина и масса), соединенные последовательно. Пусть выходом данной системы считается перемещение x(t ), тогда импеданс равен: Z ( p) = mp2 + k + Bp . Если выходом

23

Тема 4 Импеданс динамической системы

считается скорость v(t ), то Z (p) = mp + k + B = mp 2 + Bp + k . p p

Пример 4.3. Найти импеданс электрической системы (рис. 4.5).

R

L

C

Рис. 4.5 – Схема динамической системы для примера 4.3

Решение. В системе присутствуют 3 элемента, соединенные параллельно, значит, импеданс системы Z (p) определяется по формуле:

Пример 4.4. Найти импеданс электрической системы (рис. 4.6).

R C L 4R

Рис. 4.6 – Схема динамической системы для примера 4.4

Решение. В данной системе присутствуют 4 элемента, соединенных последовательно, значит импеданс системы равен:

Пример 4.5. Найти импеданс электрической системы (рис. 4.7).

Рис. 4.7 – Схема динамической системы для примера 4.5

24

Тема 4 Импеданс динамической системы

Задачи для самостоятельного решения к теме 4

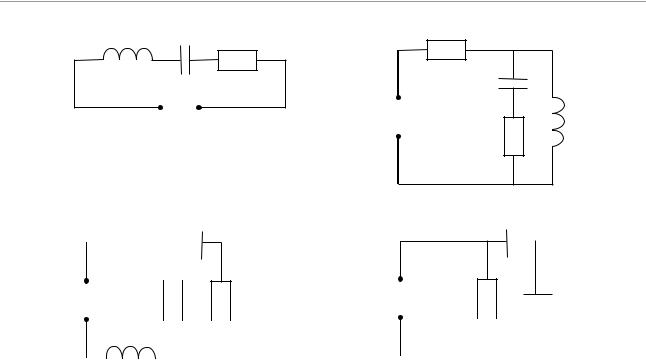
Задача 4.1. Найти импедансы следующих систем:

25

Тема 4 Импеданс динамической системы

Рис. 4.9 – Схемы динамических систем для задачи 4.1

Контрольные вопросы к теме 4

Основной уровень

1.Дайте определение импеданса электрической системы; импеданса механической системы.

2.Как рассчитать импедансы простейших электрических и механических элементов систем?

3.Сформулируйте правило расчета импедансов при последовательном и параллельном соединении элементов системы.

Углубленный уровень

1.Как рассчитывается импеданс системы, содержащей последовательно и параллельно соединенные элементы?

2.Какая аналогия существует между элементами электрических и механических систем?

26

Рис. 5.1 – Обобщенная схема динамической системы

Определение. Передаточная функция W (p ) динамической системы – это отношение преобразованной по Лапласу выходной переменной к преобразованной по Лапласу входной переменной этой системы при нулевых

начальных условиях (н. у.): W (p ) = X ( p) , где X (p) = L [x(t )], Y (p) = L [y(t)].

Y ( p)

Передаточная функция является одним из способов математического описания динамической системы и может быть рассмотрена как дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. При нулевых н. у. дифференциальное уравнение описания ДС и передаточная функция связаны взаимно-однозначно. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

Пример 5.1. Задана динамическая система в виде электрической цепи, причем вход системы – напряжение U1 (t ), выход – напряжение U 2 (t ) (рис. 5.2). Найти передаточную функцию системы и восстановить дифференциальное уравнение описания функционирования системы во времени.

U 2 (p) = L[U 2 (t )]. Для нахождения передаточной функции будем использовать импеданс системы.

27

Тема 5 Передаточная функция

Рассмотрим импеданс всей системы: Z (p ) = R + 1 = RCp + 1 .

Cp Cp

С другой стороны, по определению импеданса электрических систем,

Z12 (p) один и тот же, так как цепь представляет собой последовательное

Tp + 1

Восстановим дифференциальное уравнение данной системы по передаточной функции. Для этого воспользуемся найденным значение W (p) и определением передаточной функции.

U1 (p) = (Tp + 1)U 2 ( p) .

Последнее равенство является операторным уравнением системы. Взяв обратное преобразование Лапласа от операторного уравнения при нулевых начальных условиях, получим искомое дифференциальное уравнение:

Пример 5.2. Для заданной динамической системы (рис. 5.3) найти передаточную функцию и восстановить дифференциальное уравнение описания функционирования системы во времени.

28

Тема 5 Передаточная функция

U1 ( p) = Z ( p) i ( p) = (Lp + R) i ( p) .

передаточную функцию приведем к стандартному виду – в числителе и знаменателе свободный коэффициент должен равняться 1: