Определение моментов инерции твердых тел с помощью трифилярного подвеса

Принадлежности: трифилярный подвес; секундомер; счетчик числа колебаний; штангенциркуль; набор тел, подлежащих измерению (диск, стержень, полый цилиндр и т. д.).

Момент инерции J твердого тела относительно некоторой оси определяется выражением

,

где r — расстояние элемента массы dm от оси вращения.

В простых случаях величину момента инерции можно определять расчетом, а в сложных — его приходится находить экспериментальным путем. Одним из удобных методов измерения моментов инерции твердых тел является метод трифилярного подвеса. Устройство такого подвеса показано на рис. 1. Подвижная платформа P΄ подвешена к платформе P на трех симметрично расположенных нитях AA΄, BB' и СС'. Платформа P укреплена па кронштейне и снабжена рычагом (на чертеже не показан), при помощи которого системе можно сообщать крутильные колебания. Если повернуть нижнюю платформу Р' вокруг вертикальной оси на некоторый угол  относительно верхней, то возникает момент сил, стремящийся вернуть платформу в положение равновесия. В результате этого платформа начинает совершать крутильные колебания.

Рассмотрим теорию трифилярного подвеса. Если пренебречь трением, то на основании закона сохранения энергии для колеблющейся платформы можно написать следующее уравнение:

, (1)

где J — момент инерции платформы вместе с исследуемым телом, М — масса платформы с телом, Е—полная энергия системы, z₀ — начальная координата точки О' (при  = 0), z — координата точки О' при текущем значении . Точкой обозначено дифференцирование по времени.

Р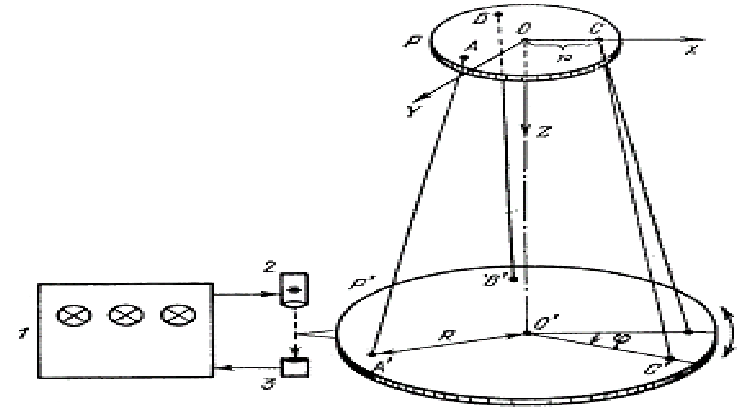ис. 1. Трифилярный подвес. 1 — пересчетное устройство, 2 — осветитель, 3 — фотоэлемент.

Как следует из рис. 1, координаты точки С равны (r, 0, 0), а точка С' имеет координаты (R соs , R sin ). Расстояние между точками С и С' равно длине нити l.

Поэтому , или

. (2)

При написании (2) было принято во внимание, что для малых углов соs. Извлекая корень из выражения (2), найдем, что при малых 

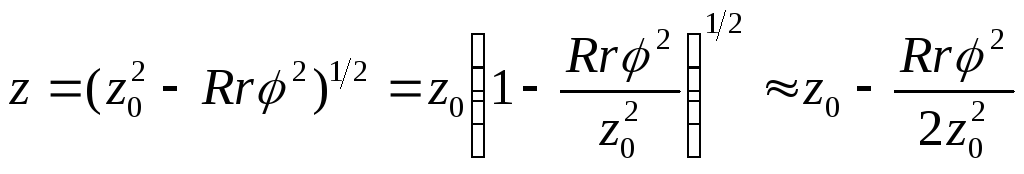. (3)

Подставив это значение z в уравнение (1), получим:

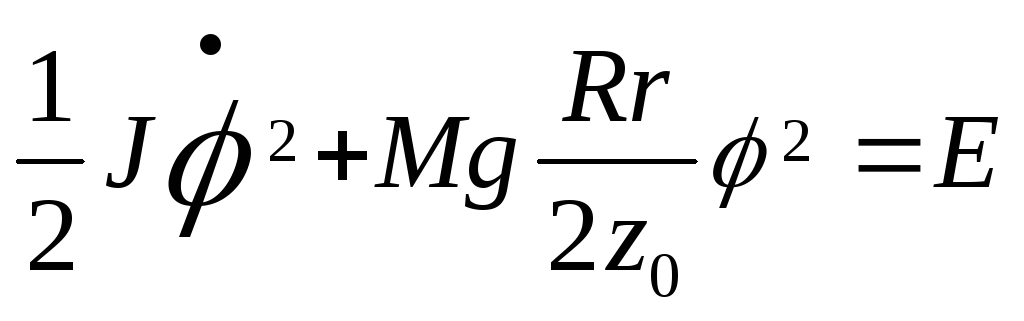. (4)

Продифференцировав последнее выражение по времени и сократив на , получим уравнение движения системы:

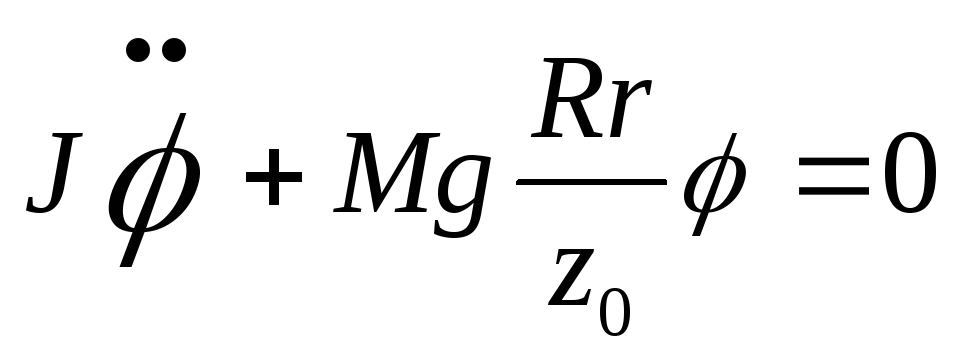. (5)

Нетрудно убедиться непосредственной подстановкой, что решение этого уравнения имеет вид:

, (6)

где амплитуда ₀ и фаза  определяются начальными условиями. Период колебаний системы Т, следовательно, равен:

. (7)

Разрешив (7) относительно J, найдем выражение для момента инерции:

. (8)

Учитывая, что параметры прибора (R, r, z₀) во время опыта не меняются, формулу (8) удобно записать в виде:

, где (9)

k для данного прибора постоянно. Формула (9) позволяет вычислить момент инерции платформы с телом и без него по измеренной величине периода Т.

Как следует из вывода, формула (8) справедлива при отсутствии потерь энергии на трение. Учет таких потерь весьма затруднителен. Однако поправки оказываются небольшими, если потери энергии за период малы по сравнению с энергией колебаний системы. Таким образом, формула (8), а вместе с ней и (9), справедлива, если

, (10)

где  — время, в течение которого амплитуда колебаний платформы существенно уменьшается (в 2 — 3 раза).

В данной работе значения Т рекомендуется измерять с точностью не хуже чем 0,5%. Этим условием определяется время и полное число колебаний платформы, которое необходимо отсчитать в процессе измерений.

Для счета числа колебаний используется счетчик, состоящий из осветителя, фотоэлемента и пересчетного устройства (см. рис. 1). Легкий лепесток, укрепленный на платформе, пересекает световой луч дважды за период. Соответствующие сигналы от фотоэлемента поступают на пересчетный прибор. Если п₁ и п₂ — начальное и конечное значения показаний прибора, то за время наблюдения измеренное число периодов равно N=(п₂ — п₁)/2, а период колебаний равен Т = t/N. Для уменьшения ошибки секундомер лучше всего включать и выключать в момент прохождения маятника через положение равновесия (в этот момент лепесток пересекает световой луч).