
Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 2 / Глава 2 / Параграф 2.12
.doc2.12. Критерий полноты (теорема Поста)
Классы
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() называют классами Поста.
называют классами Поста.
Утверждение 1. Классы Поста неполны и попарно различны.
Доказательство. Предположим, что какой-то из классов Поста полон. Тогда любая функция принадлежит его замыканию, а, следовательно, в силу его замкнутости, и ему самому. Но это не так. Например, штрих Шеффера не принадлежит ни одному из классов Поста.
Чтобы убедиться в попарном различии
классов Поста, составим таблицу, столбцы
которой соответствуют классам
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
строки – функциям
,
строки – функциям
![]() ,
а в клетках проставляется «+» или «–»
в зависимости от того, принадлежит ли
функция соответствующему классу или
не принадлежит.
,
а в клетках проставляется «+» или «–»
в зависимости от того, принадлежит ли
функция соответствующему классу или
не принадлежит.
|
|
|
|
|
|
|
|
|
+ |
– |
– |
+ |
+ |
|
|
– |
+ |
– |
+ |
+ |
|
|
– |
– |
+ |
– |
+ |
Теорема (Поста). Для того чтобы
система функций
![]() была полна, необходимо и достаточно,
чтобы множество
была полна, необходимо и достаточно,
чтобы множество
![]() не являлось подмножеством ни одного из
классов Поста.
не являлось подмножеством ни одного из
классов Поста.
Доказательство. Необходимость.
Пусть система
![]() полна. Докажем, что
полна. Докажем, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Доказательство проведем от противного:
предположим, что
.
Доказательство проведем от противного:
предположим, что
![]() - подмножество одного из классов Поста.
Обозначим этот класс
- подмножество одного из классов Поста.
Обозначим этот класс
![]() .
Имеем:
.
Имеем:
![]() .
.
Следовательно,
![]() .
т.е.
.
т.е.
![]() .
Но это не так, хотя бы потому, что штрих
Шеффера не принадлежит ни одному из
классов Поста. Получили противоречие,
следовательно, наше предположение было
неверным.
.
Но это не так, хотя бы потому, что штрих
Шеффера не принадлежит ни одному из
классов Поста. Получили противоречие,
следовательно, наше предположение было
неверным.
Достаточность.
Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .Тогда
найдутся функции
.Тогда
найдутся функции
![]() такие, что
такие, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Покажем, что отрицание и конъюнкцию
можно реализовать формулами над
множеством
.
Покажем, что отрицание и конъюнкцию
можно реализовать формулами над
множеством
![]() .
Процедуру построения соответствующих
формул покажем в виде схемы:
.
Процедуру построения соответствующих
формул покажем в виде схемы:
Т аким
образом, конъюнкцию и отрицание можно
реализовать формулой над
аким
образом, конъюнкцию и отрицание можно
реализовать формулой над
![]() .
Имеем:
.
Имеем:
![]() - полная система, причем каждая ее функция
может быть выражена формулой над
- полная система, причем каждая ее функция
может быть выражена формулой над
![]() .
Следовательно, условия теоремы о полноте
выполнены и, значит,
.
Следовательно, условия теоремы о полноте
выполнены и, значит,
![]() - полная система. ■
- полная система. ■
Следствие. Всякий замкнутый
класс функций, не совпадающий с
![]() ,
содержится, по крайней мере, в одном из
классов Поста.
,
содержится, по крайней мере, в одном из
классов Поста.
Определение. Класс
![]() называется предполным
классом, если:
называется предполным
классом, если:
-
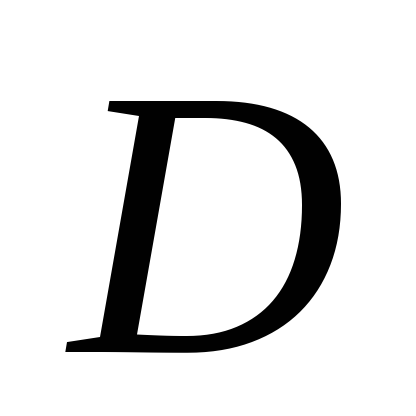 неполон;
неполон; -
добавление к
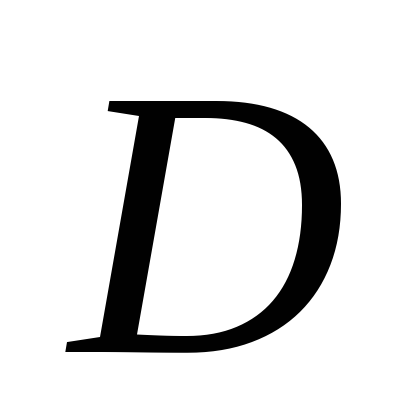 любой функции, ему не принадлежащей,
приводит к образованию полного множества.
любой функции, ему не принадлежащей,
приводит к образованию полного множества.
Справедливо утверждение, которое мы приводим без доказательства.
Утверждение 2. Предполными являются классы Поста и только они.
Определение. Система функций
![]() называется
базисом,
если:
называется
базисом,
если:
1.
![]() -полна;
-полна;
2. при удалении из системы
![]() хотя бы одной функции, полнота теряется.
хотя бы одной функции, полнота теряется.
Примеры.
1.
![]() - дизъюнктивный базис Буля.
- дизъюнктивный базис Буля.
2.
![]() - конъюнктивный базис Буля.
- конъюнктивный базис Буля.
3.
![]() - базис Шеффера.
- базис Шеффера.
4.
![]() - базис Жегалкина.
- базис Жегалкина.
