
Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 2 / Глава 2 / параграф 2.3 2
.4.doc2.3. Двойственные функции
Определение. Функция, реализуемая
формулой
![]() ,
называется двойственной
к функции
,
называется двойственной
к функции
![]() .
.
Функцию, двойственную к функции
![]() ,
обозначают
,
обозначают
![]() ,
т.е.
,
т.е.
![]() .
.
Пример 1.
а) Пусть
![]() .
Тогда
.
Тогда
![]() .
.
б) Пусть
![]() .
Тогда
.
Тогда
![]() .
.
в) Пусть
![]() .
Тогда
.
Тогда
![]() .
.
г) Пусть
![]() .
Тогда
.
Тогда
![]() .
.
д) Пусть
![]() .
Тогда
.
Тогда
![]() .
.
е) Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Замечание.
Рассмотрим таблицы истинности для
произвольной функции двух переменных
![]() и двойственной к ней функции
и двойственной к ней функции
![]() :
:
|
|
|
|
|
|
0 |
0 |
|
|
|
0 |
1 |
|
|
|
1 |
0 |
|
|
|
1 |
1 |
|
|
Нетрудно заметить, что столбец значений
функции
![]() может быть получен из столбца значений
функции
может быть получен из столбца значений
функции
![]() ,
если действовать по такому алгоритму:
,
если действовать по такому алгоритму:
-
каждое число, стоящее в столбце значений, заменить на противоположенное (0 на 1 и 1 на 0);
-
получившийся в результате выполнения пункта 1 столбец переписать в обратном направлении (т.е. число, стоящее в первой строке, записать в последнюю строку; число, стоящее во второй строке - в предпоследнюю строку и т.д.).
Аналогичного алгоритма для получения двойственной функции можно придерживаться и в случае любого числа аргументов.
Утверждение.
![]() .
.
Доказательство.
![]()
![]() .
■
.
■
Лемма. Если формула
![]() реализует функцию
реализует функцию
![]() ,
то формула
,
то формула
![]() реализует функцию
реализует функцию
![]() .
.
Доказательство.
![]()
![]()
![]()
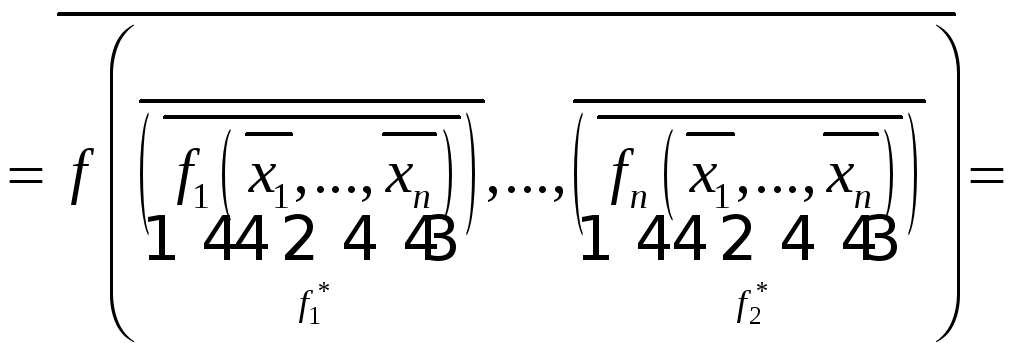
![]()
![]() .
■
.
■
Справедливо следующее утверждение, которое приведем без доказательства.
Теорема (принцип двойственности).
Если формула
![]() реализует функцию
реализует функцию
![]() ,
то формула, полученная из нее заменой
символов функций
,
то формула, полученная из нее заменой
символов функций
![]() на символы двойственных к ним функций
на символы двойственных к ним функций
![]() ,
реализует функцию
,
реализует функцию![]() ,
двойственную к функции
,
двойственную к функции
![]() (эту формулу будем называть двойственной
к
(эту формулу будем называть двойственной
к
![]() и обозначать
и обозначать
![]() ).
).
Заметим, что доказательство этой теоремы основано на лемме и проводится индукцией по структуре формул.
Следствие. Поскольку
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
,
![]() ,
,
![]() (пример 1), то для получения формулы,
двойственной к формуле
(пример 1), то для получения формулы,
двойственной к формуле
![]() ,
нужно в формуле
,
нужно в формуле
![]() заменить 0 на 1, 1 на 0, связку
заменить 0 на 1, 1 на 0, связку
![]() на связку
на связку
![]() ,
связку
,
связку
![]() на связку
на связку
![]() .
.
Пример 2.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
2.4. Разложение булевых функций по переменным
Введем обозначение:
![]() Следовательно, имеем:
Следовательно, имеем:
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Таким образом, верно:
![]() .
.
Теорема 1 (о разложении функций по
переменным). Каждую булеву
функцию
![]() при любом
при любом
![]()
![]() можно реализовать формулой:
можно реализовать формулой:
![]() .
(1)
.
(1)
Доказательство. Возьмем
произвольный набор
![]() значений переменных и найдем на этом
наборе значение функции, реализуемой
формулой (1):
значений переменных и найдем на этом
наборе значение функции, реализуемой
формулой (1):
![]()


![]() .
.
(*):
![]()
![]() .
.
Таким образом, имеем:
![]()
![]() .
■
.
■
Следствия. 1. Разложение функции по одной переменной:
![]() .
.
2. Разложение функции по всем переменным:
![]() .
(2)
.
(2)
Теорема 2 (о реализации функции в виде
СДНФ). Если
![]() ,
то она может быть реализована формулой
,
то она может быть реализована формулой
![]() .
(3)
.
(3)
Формулу (3) называют совершенной дизъюнктивной нормальной формой или, сокращенно, СДНФ.
Доказательство.
![]()


![]() .
■
.
■
Пример 1. а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
Теорема 3 (о реализации функции в виде
СКНФ). Если
![]() ,
то она может быть реализована формулой
,
то она может быть реализована формулой
![]() .
.
Формулу (4) называют совершенной конъюнктивной нормальной формой или, сокращенно, СКНФ.
Доказательство. Реализуем
функцию
![]() ,
двойственную к
,
двойственную к
![]() ,
в виде СДНФ.
,
в виде СДНФ.
![]() .
.
Следовательно,


 .
■
.
■
Пример 2. а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Утверждение. Каждая булева функция
может быть реализована формулой над
множеством
![]() .
.
Доказательство. Возможны два случая:
1.
![]() .
Тогда
.
Тогда
![]() и может быть реализована в виде СКНФ.
и может быть реализована в виде СКНФ.
2.
![]() .
Тогда
.
Тогда
![]() может быть реализована в виде СДНФ.
■
может быть реализована в виде СДНФ.
■
