
Курс лекций по высшей математике. 1 часть
.pdf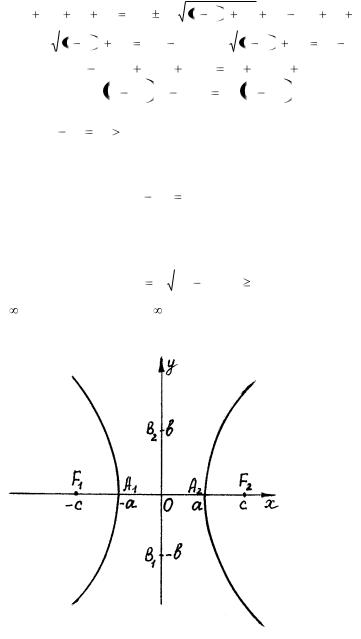
х 2 2сх с 2 |
у 2 |
4а 2 4а х с 2 у 2 |
х 2 |
2сх с 2 |
у 2 ; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
4а х с 2 у 2 |
4а 2 |
4сх ; а х с 2 |
у 2 а 2 |
сх ; |
|||||||||
а 2 х 2 |
2а 2сх а 2с2 |
а 2 у2 |
а 4 |
2а 2сх с2 х 2 ; |
|
||||||||
|
|
с2 |
а 2 х 2 |
а 2 у2 |
а 2 с2 |
а 2 . |
|
|
|
||||
Обозначив с2 а 2 |
в2 |
0 и разделив обе части на а2в2, получим кано- |
|||||||||||
ническое уравнение гиперболы: |
|
|
|
|
|
|
|
||||||
|
|
|
х 2 |
|
у2 |
1. |
|
|
|
|
|
(2.23) |
|
|
|
|
а 2 |
|
в2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Кривая симметрична относительно осей координат, так как уравнение содержит только четные степени х, у. В первой координатной чет-
|
в |
|
|
|
|
|
верти уравнение имеет вид у |
|
х 2 |
а 2 , х а; при возрастании х от |
|||
|
|
|||||
а |
||||||
|
|
|
|
|
||
а до + у возрастает от 0 до + |
. Учитывая симметрию, можно сделать |
|||||
вывод о форме гиперболы (рис. 30). |
|
|
||||
Рис. 30
63
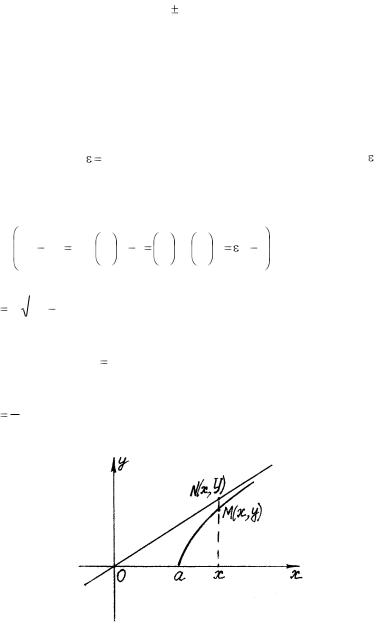
Полагая в каноническом уравнении у = 0, найдем точки пересечения гиперболы с осью ОХ: х = а. При х = 0 уравнение не имеет решений, то есть с осью ОУ гипербола не пересекается. Точки А1(-а; 0) и А2(а; 0) называются вершинами гиперболы. Фокальная ось (ось, на которой лежат фокусы) называется действительной осью гиперболы, а перпендикулярная ей ось – мнимой осью. Действительной осью называется также отрезок А1А2 и его длина 2а. Отрезок, соединяющий точки В1(0; -в) и В2(0; в), а также его длина 2в называются мнимой осью гиперболы. Числа а и в называются соответственно действительной и мнимой полуосями.
Отношение |
с |
называется эксцентриситетом гиперболы. > 1. |
|
а |
|||
|
|
Эксцентриситет характеризует форму гиперболы: чем меньше эксцентриситет, тем меньше отношение полуосей гиперболы, то есть тем сильнее вытянут ее основной прямоугольник относительно фокальной
оси с 2 а 2 в 2 ; |
с |
2 |
1 |
в 2 |
; |
в 2 |
2 1 . |
||
а |
|
а |
|
а |
|
||||
|
|
|
|
|
|||||
Рассмотрим часть гиперболы, расположенную в первой четверти:
|
в |
|
|
|
|
|
у |
|
х 2 |
а 2 . Покажем, что точки этого графика, расположенные на |
|||
|
|
|||||
а |
||||||
|
|
|
|
|
||
достаточно большом расстоянии от начала координат, сколь угодно
близки к прямой у |
в |
х . Пусть М(х, у) и N(х, У) – точки с одной и той |
|
а |
|||
|
|
же абсциссой, лежащие соответственно на гиперболе и на прямой
уав х (рис. 31). Рассмотрим разность ординат этих точек:
Рис. 31
64
|
|
|
|
|
|
в |
|
|
в |
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
У у |
|
х |
|
х 2 а 2 |
х |
|
х 2 |
а 2 |
|
|
|
|||||||||||||||||
|
|
|
|
а |
|
а |
а |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в |
|
х |
х 2 а 2 |
|
|
х |
|
|
|
х 2 |
а 2 |
|
а 2 |
|
|
|
|
|
ав |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
. |
|||||
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а х |
|
|
|
|
|
|
|
|
|
|
||||
|
|
х |
х 2 |
|
а 2 |
|
|
|
|
|
х 2 |
а 2 х |
х 2 а 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
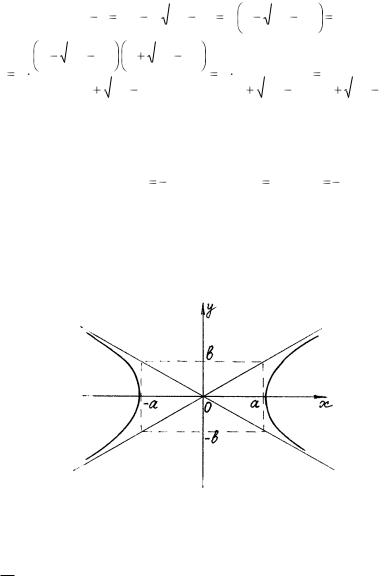
Очевидно, что при неограниченном возрастании х эта разность стремится к нулю, то есть точки М и N неограниченно сближаются. Из симметрии гиперболы относительно осей координат следует, что этим же свой-
ством обладает прямая у |
в |
х . Прямые |
у |
в |
х и |
у |
в |
х называ- |
|
а |
а |
а |
|||||||
|
|
|
|
|
|
ются асимптотами гиперболы.
На рисунке 32 показано, как с помощью основного прямоугольника гиперболы (это прямоугольник со сторонами длиной 2а и 2в, параллельными осями координат) построить асимптоты гиперболы. Из рисунка видно также взаимное расположение гиперболы и ее асимптот.
Рис. 32
Пример 15. Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами равно 26, а эксцентриситет равен
1213 .
65

|
|
Решение. По условию 2с = 26, |
|
|
с |
|
13 |
. Следовательно, большая |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
а |
|
12 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
полуось |
|
гиперболы |
а |
с |
13 |
12 |
|
12. |
|
|
Тогда малая полуось |
||||||||
|
13 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в |
|
с 2 |
|
а 2 |
132 12 2 |
5. |
Уравнение |
гиперболы имеет вид |
|||||||||||
|
х 2 |
|
|
у |
2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
144 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Парабола
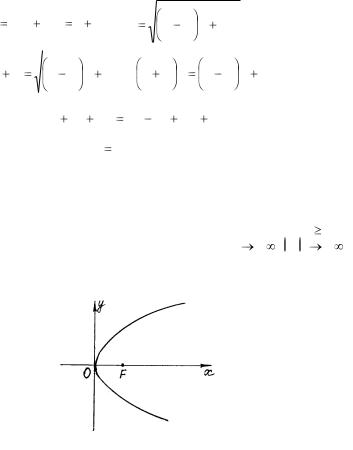
Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Обозначим фокус F, расстояние от фокуса до директрисы р. Выберем декартову прямоугольную систему координат так, чтобы ось ОХ проходила через фокус перпендикулярно директрисе в направлении от директрисы к фокусу и начало координат делило пополам расстояние
между фокусом и директрисой (рис. 33). Тогда F р2 ; 0 , а уравнение
директрисы х  р2 .
р2 .
Рис. 33
66
Выведем уравнение параболы в выбранной системе координат. Пусть М(х, у) – произвольная точка параболы, МN – перпендикуляр, опущенный из точки М на директрису.
По определению МN = МF.
Но М N М Q QN х |
|
р |
, |
МF |
|
х |
|
|
р 2 |
у 2 . |
|||||||||||
|
2 |
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|||
|
р |
|
|
р |
2 |
|
|
|
|
|
|
р |
|
|
|
р |
|||||
Тогда х |
|
|
х |
|
|
|
|
|
у2 ; х |
|
|
|
|
|
|
х |
|
|
у 2 ; |
||
2 |
|
2 |
|
|
|
|
2 |
|
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
р 2 |
|
|
|
|
|
р 2 |
|
|
|
||||
|
|
|
х 2 рх |
|
|
|
|
|
х 2 |
рх |
|
|
|
|
у 2 , |
или |
|||||
|
|
|
4 |
|
4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
у2 |
|
2рх |
|
|
|
|
|
|
|
|
|
(2.24) |
|||
– каноническое уравнение параболы.
Уравнение содержит у лишь в четной степени, следовательно, кривая симметрична относительно оси ОХ. При х = 0 у = 0, то есть парабо-
ла проходит через начало координат. Из уравнения следует, что х |
0 – |
||
кривая располагается в правой полуплоскости. При х |
+ |
у |
+ |
(рис. 34). Ось симметрии параболы называется ее фокальной осью, точка 0 – вершиной параболы.
Рис. 34
Замечание. При другом выборе системы координат получаются канонические уравнения другого вида (рис. 35, 36, 37).
67
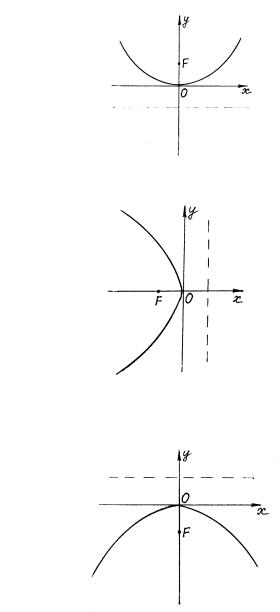
х2=2ру
Рис. 35
у2=–2рх
Рис. 36
х2=–2ру
Рис. 37
68

Общее уравнение кривой второго порядка
Общее уравнение кривой второго порядка имеет вид
Ах2 Вху Су2 Дх Еу F 0.
Уравнение такого вида может определять: 1) эллипс (в частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых (параллельных, пересекающихся либо совпадающих), 5) точку или не определять никакой линии.
В простейшем случае, при В = 0, тип кривой можно определить, выделив полные квадраты переменных.
Пример 16. Построить кривую х 2 |
|
2у2 |
2х |
12у |
33 |
0. |
|
|||||||||||
Решение. |
|
х2 |
2х |
х2 |
2х |
1 |
|
1 |
х |
1 2 |
1; |
|
2у2 |
12у |
||||
2 у2 |
6у |
2 у2 |
6у |
9 |
9 |
2 |
|
у |
3 2 |
18. |
|
Тогда |
уравнение |
|||||
можно |
записать |
в |
виде |
х |
1 2 |
|
1 2 у 3 2 |
18 |
33 |
0 , |
или |
|||||||
х 1 2 |
2 у |
3 2 |
16 , |
или |
|
х |
1 2 |
|
|
|
у |
3 2 |
1 – уравнение гипербо- |
|||||
|
|
16 |
|
|
|
|
8 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лы с полуосями а = 4, в 2
 2, центр которой находится в точке О1(-1;
2, центр которой находится в точке О1(-1;
3) (рис. 38).
Рис. 38
69
§ 12. Полярная система координат
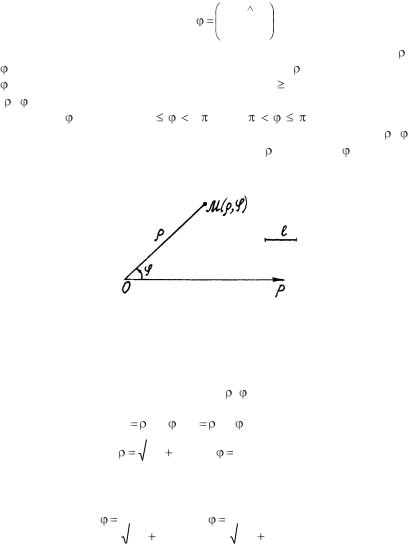
Полярная система координат на плоскости определяется заданием некоторой точки О, называемой полюсом, луча Ор, исходящего из этой точки и называемого полярной осью, и единицы масштаба (рис. 39).
Пусть М – произвольная точка плоскости. Обозначим  = ОМ –
= ОМ –
расстояние точки М от полюса, О М, Ор – угол, отсчитываемый
от полярной оси против часовой стрелки до направления ОМ. Числа и называются полярными координатами точки М, – полярный радиус,
– полярный угол точки М. По определению  0. Задание пары чисел
0. Задание пары чисел
( , ) однозначно определяет точку М на плоскости. |
Если ограничить |
||
изменение пределами 0 |
2 (или - |
), |
то каждой точке |
плоскости также будет однозначно соответствовать пара чисел ( , ). Исключение составляет полюс, для которого = 0, а угол не определен.
Рис. 39
Выберем декартову систему координат так, чтобы ее начало 0 совпадало с полюсом, а ось ОХ была направлена по полярной оси Ор (рис.40). Тогда полярные координаты ( , ) и декартовы координаты (х, у) точки М связаны соотношениями:
х |
cos |
, |
|
у |
sin |
; |
(2.25) |
|||
|
|
|
|
|
|
|
|
у |
|
|
|
|
2 |
|
2 |
|
|
|
(2.26) |
||
|
|
|
|
|
|
|
|
|||
|
х |
|
у |
|
, |
tg |
х . |
|||
|
|
|
|
|||||||
Из этих формул следует:
cos |
|
|
x |
|
|
, sin |
|
|
у |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(2.27) |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||||||
|
|
х 2 |
|
у 2 |
х 2 |
|
у 2 |
|
|
||||
|
|
|
|
|
|
|
|||||||
70
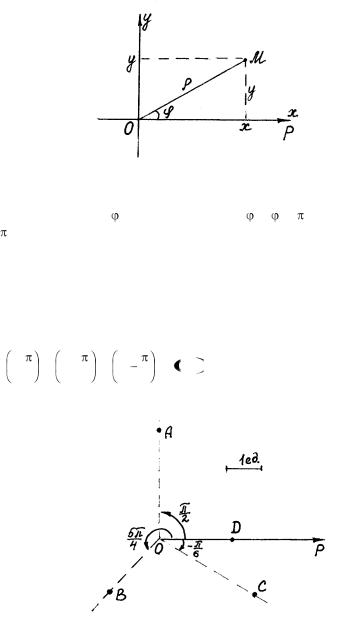
Рис. 40
Формула для tg определяет два угла и + в промежутке [0; 2 ). Чтобы уточнить, какой из углов выбрать, нужно учесть четверть, в которой находится точка М, или воспользоваться формулами (2.27).
Чтобы перейти от уравнения линии в декартовых координатах к ее полярному уравнению, нужно вместо х, у подставить в уравнение их выражения из формул (2.25). Обратный переход от полярного уравнения к уравнению в декартовых координатах осуществляется с помощью
формул (2.26), (2.27). |
|
|
|||||
Пример |
17. |
Построить в полярной системе координат точки |
|||||
А 3; |
|
, В 2; |
5 |
|
, С 3; |
|
, Д 2; 0 . |
|
|
|
|
||||
2 |
|
4 |
|
|
6 |
|
|
Решение. Построение точек показано на рис. 41
Рис. 41
71

Пример 18. Какие линии определяются уравнениями |
= а(const) и |
= (const)? |
|
Решение. Геометрическое место точек, для которых |
– расстояние |
от полюса – постоянно, есть окружность, поэтому уравнение = а опре-
деляет окружность радиуса а с центром в полюсе 0. Уравнение |
= |
|||
определяет луч, выходящий из полюса под углом к полярной оси. |
|
|||
Пример 19. Дано полярное уравнение линии |
|
|
|
По- |
3 sin 2 . |
||||
строить эту линию по точкам. Найти ее декартово уравнение, расположив систему Охy так, как показано на рис.40
|
Решение. Выражение в правой части имеет смысл при sin2 |
0, то |
||||||||||||||||||||||||||
есть |
0 |
|
|
|
и |
3 |
|
. Учитывая периодичность функции (период |
||||||||||||||||||||
2 |
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Т = |
), достаточно рассмотреть |
0 |
|
|
|
. Составим таблицу значений |
||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||
функции, ограничиваясь точностью 0,01: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
6 |
|
|
4 |
|
3 |
|
12 |
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0 |
|
2,12 |
|
2,79 |
|
3 |
|
2,79 |
2,12 |
0 |
|
||||||||||||
|
3 sin 2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведем лучи, соответствующие выбранным значениям , и на каждом из них отложим вычисленное значение . Полученные точки соединим плавной кривой (рис. 42). Построенная линия называется лемнискатой Бернулли. Чтобы перейти к декартовым координатам, за-
пишем уравнение в виде |
2 |
|
9 2 sin |
cos |
|
и воспользуемся формула- |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
у |
|
|
|
х |
|
|
ми |
(2.26) |
и |
|
(2.27): |
|
|
|
х 2 |
у 2 |
18 |
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
х 2 у2 |
|
|
|
х 2 у 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
х 2 |
у2 |
18ху |
; |
х 2 у 2 |
2 |
18ху |
– уравнение линии в декартовой |
||||||||||||||
|
|
|
|||||||||||||||||||
х 2 |
у2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
системе координат.
72
