
Курс лекций по высшей математике. 1 часть
.pdf
3.2. Матричный метод решения систем
Введем матрицу системы
|
|
|
|
а11 |
a12 ... |
a1n |
|
|
|
А |
а21 |
a22 ... |
a2n |
|
|
|
... ... ... ... |
|||
|
|
|
|
|||
|
|
|
|
аn1 |
an2 ... |
ann |
|
x1 |
|
b1 |
|
|
|
и матрицы |
x2 |
и |
b2 |
. Пусть det A |
0 . |
|
|
... |
|
... |
|
|
|
xn bn
Представим систему (1.10) в виде матричного уравнения АХ=В. Это легко проверить, перемножив матрицы А и Х.
Действительно,
|
а11 |
а12 |
... |
a1n |
x1 |
|
|
А Х |
a21 |
a22 |
... |
a2n |
x2 |
|
|
... ... ... ... |
... |
|
|||||
|
|
||||||
|
an1 an2 |
... |
ann |
xn |
|
||
a11x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
||
a21x1 |
a22 x2 |
... |
a2n xn |
b2 |
B. |
||
.......... .......... .......... ....... |
... |
||||||
|
|||||||
an1x1 |
an2 x2 |
... |
ann xn |
bn |
|
||
Решим теперь матричное уравнение А·Х=В. Умножим обе части
уравнения на матрицу А-1 слева. Тогда А-1·А·Х = А-1·В, а так как А-1·А=Е, то имеем Е·Х=А-1·В и, наконец,
Х = А-1·В (1.12)
Пример 17. Матричным методом решить систему уравнений
x |
y |
2z |
6, |
2x |
3y |
7z |
16, |
5x |
2 y |
z |
16. |
Решение. Вычислим определитель матрицы А.
1 1 2
det A 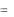 2 3 7 2 0, 5 2 1
2 3 7 2 0, 5 2 1
то есть матрица А невырожденная. Построим обратную матрицу А-1. Вычислим алгебраические дополнения элементов матрицы А:
23
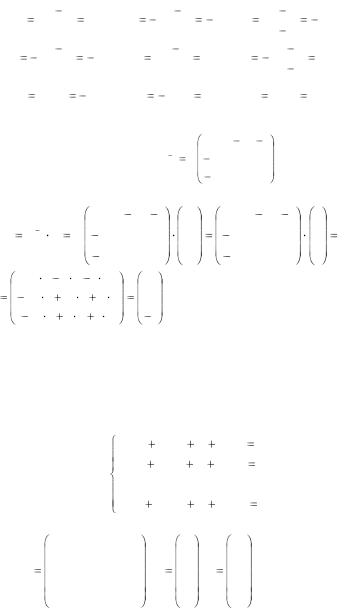
А11 |
|
3 |
7 |
|
17, |
|
А21 |
|
1 |
|
2 |
|
5, |
А31 |
|
1 |
|
2 |
|
1, |
|||||||
|
2 |
1 |
|
|
|
2 |
|
1 |
|
|
|
3 |
|
7 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
А12 |
|
|
7 |
|
|
|
37, |
|
А22 |
|
1 |
|
2 |
|
|
11, |
А32 |
|
1 |
2 |
|
3, |
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
5 |
1 |
|
|
|
|
|
5 |
|
1 |
|
|
|
|
2 |
7 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
А13 |
|
3 |
|
|
11, |
|
А23 |
|
|
1 |
1 |
|
|
3, |
А33 |
|
1 |
1 |
|
1, |
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
5 |
2 |
|
|
|
|
|
5 |
2 |
|
|
|
|
|
2 |
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
17 |
5 |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
А 1 |
37 |
11 |
3 . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
3 |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Находим теперь решение системы по формуле (1.12). |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
17 |
|
5 |
|
1 |
|
6 |
|
17 |
5 |
|
1 |
3 |
||||||
Х А 1 |
В |
|
|
37 |
11 |
3 |
|
16 |
|
37 |
11 |
|
|
3 |
|
8 |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
11 |
3 |
1 |
|
16 |
|
11 |
3 |
|
|
1 |
|
8 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
17 |
|
3 |
5 |
8 |
|
1 8 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
37 |
|
3 |
11 |
8 |
3 |
8 |
|
1 |
, |
то есть x = 3, y = 1, z = -1. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
11 |
3 |
3 8 |
1 8 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
§ 4. Произвольные системы линейных уравнений
4.1. Определения
Пусть задана система m линейных уравнений с n неизвестными общего вида
|
|
|
|
|
а11х1 |
а12 х2 ... |
а1n хn |
b1, |
|
|
|
|
|
|
|
а21х1 |
а22 х2 ... |
а2n хn |
b2 , |
(1.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......... .......... .......... .......... ......, |
|
||||
|
|
|
|
|
аm1х1 |
аm2 х2 ... |
аmn хn |
bm . |
|
|
или, в матричной форме, А·Х = В, |
|
|
|
|||||||
|
|
a11 |
a12 |
... |
a1n |
|
x1 |
b1 |
|
|
где |
|
a21 |
a22 |
... |
a2n |
|
x2 |
b2 |
|
|
|
А |
... ... ... ... |
, X |
... , B |
... . |
|
|
|||
|
|
am1 |
am2 |
... |
amn |
|
xn |
bm |
|
|
Если В=0, то система называется однородной, в противном случае она называется неоднородной.
24

Решением системы называется совокупность значений неизвестных х1=α1, х2=α2, …, хn=αn, при подстановке которых все уравнения системы обращаются в равенства.
Система, имеющая хоть одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовмест-
ной.
Система, имеющая единственное решение, называется определен-
ной.
Система, имеющая более одного решения, называется неопределенной.
Назовем расширенной матрицей системы матрицу, полученную из А добавлением к ней столбца свободных членов системы:
|
|
а11 |
а12 |
... |
a1n |
b1 |
|
|
|
а21 |
а22 |
... |
a2n |
b2 |
(1.14) |
|
|
||||||
А |
... ... ... ... |
... . |
|
||||
|
|
am1 |
am2 |
... |
amn |
bm |
|
Так как каждый минор матрицы А является и минором матрицы A , но не наоборот, то r( A) r( A).
4.2. Теорема Кронекера-Капелли
Для того чтобы система m неоднородных линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы
r( A) r( A).
Доказательство необходимости.
Пусть система (1.13) совместна, то есть существуют такие числа
х1=α1, х2=α2, …, хn=αn, что
a11 |
1 |
a12 |
2 |
... |
a1n |
n |
b1, |
|
a21 |
1 |
a22 |
2 |
... |
a2n |
n |
b2 , |
(1.15) |
|
|
|
|
|
|
|
|
|
.......... .......... .......... .......... ........ |
|
|||||||
am1 |
1 |
am2 |
2 |
... |
amn |
n |
bm , |
|
Вычтем из последнего столбца расширенной матрицы A ее первый столбец, умноженный на α1, второй – на α2, …, n-ый – умноженный на αn, то есть из последнего столбца матрицы (1.14) следует вычесть левые части равенств (1.15). Тогда получим матрицу
|
а11 |
а12 |
... |
a1n |
0 |
|
С |
а21 |
а22 |
... |
a2n |
0 |
, |
... |
... |
... |
... |
... |
||
|
am1 |
am2 |
... |
amn |
0 |
|
25

ранг которой в результате элементарных преобразований не изменится и r(C) r( A ) . Но очевидно, r(C) r( A) и, значит, r( A) r( A).
Доказательство достаточности.
Пусть r(A) r(A) r и пусть для определенности не равный нулю минор порядка r расположен в левом верхнем углу матрицы:
|
a11 |
a12 |
... |
a1r |
|
|
M |
a21 |
a22 |
... |
a2r |
0. |
|
... ... ... ... |
||||||
|
|
|||||
|
ar1 |
ar 2 |
... |
arr |
|
|
Это означает, что остальные строки матрицы A могут быть получены как линейные комбинации первых r строк, то есть m-r строк матрицы можно представить в виде сумм первых r строк, умноженных на некоторые числа. Но тогда первые r уравнений системы (1.13) самостоятельны, а остальные являются их следствиями, то есть решение системы первых r уравнений автоматически является решением остальных уравнений.
Возможны два случая.
1.r=n. Тогда система, состоящая из первых r уравнений, имеет одинаковое число уравнений и неизвестных и совместна, причем решение ее единственно.
2.r<n. Возьмем первые r уравнений системы и оставим в левых частях этих уравнений первые r неизвестных, а остальные – перенесем вправо:
a11x1 |
a12 x2 |
... |
a1r xr |
b1 |
a1r |
1xr |
1 ... |
a1n xn , |
|
a21x1 |
a22 x2 |
... |
a2r xr |
b2 |
a2r |
1xr |
1 ... |
a2n xn , |
(1.16) |
.......... .......... .......... .......... .......... .......... .......... .......... |
|
||||||||
ar1x1 |
ar 2 x2 |
... |
arr xr |
br |
arr |
1xr |
1 ... |
ar1n xn . |
|
«Свободным» неизвестным xr+1, xr+2, …, xn можно придать какие угодно значения. Тогда соответствующие значения получают неизвестные x1, x2, …, xr. Система (1.13) и в этом случае совместная, но неопределенная.
Замечание. Отличный от нуля минор порядка r, где r<n, будем называть базисным минором. Неизвестные х1, х2, …, хr так же называют базисными, остальные – свободными. Систему (1.16) называют укороченной.
Если свободные неизвестные обозначить хr+1=c1, хr+2=c2, …, хn=cn-r, то базисные неизвестные будут от них зависеть, то есть решение систе-
мы m уравнений с n неизвестными будет иметь вид
X = (x1(c1, …, cn-r), x2(c1, …, cn-r), …, xr(c1, …, cn-r), c1, c2, …, cn-r)T,
где значок Т означает транспонирование.
Такое решение системы называется общим.
26

4.3. Метод Гаусса
Пусть требуется решить систему АХ=В. Над строками расширенной матрицы произведем элементарные преобразования, приводящие ее к виду, когда ниже элементов а11, а22, …, аrr будут стоять нули. Этот вид матрицы будем называть трапециевидным.
Отметим, что все преобразования, приводимые над строками расширенной матрицы, проводятся над соответствующими уравнениями данной системы, а, как известно, в таком случае получают равносильную данной систему уравнений.
Итак, преобразуем матрицу
|
|
|
|
|
|
|
|
|
|
a11 |
|
a12 |
|
... |
|
a1n |
b1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a21 |
|
a22 |
|
... |
|
a2n |
b2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
... ... ... ... |
... |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
am1 |
|
am2 ... |
|
amn |
bm |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a11 |
a12 |
... |
|
a1r |
|
|
a1r |
1 ... |
|
a1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
a 22/ |
... |
|
a 2/ r |
|
a 2/ r |
1 ... |
|
a 2/ n |
b2/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
к виду |
... ... ... ... ... ... ... |
... |
. |
|
|
|
|
|
|
|
|
|
|
(1.17) |
|||||||||||||
0 |
0 |
... |
|
a rr/ |
|
|
a rr/ |
1 ... |
|
a rn/ |
br/ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
0 |
... |
|
0 |
|
|
0 ... |
|
0 |
br/ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
... ... ... ... ... ... ... |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
0 |
0 |
... |
|
0 |
|
|
0 ... |
|
0 |
bm/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Матрица (1.17) является расширенной матрицей укороченной систе- |
|||||||||||||||||||||||||||
мы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11x1 |
|
a12 x 2 |
.... |
|
a1r x r |
a1r |
1 x r 1 |
|
.... |
a1n x n |
b1 , |
|
|
||||||||||||
|
|
|
|
a |
/ 22 x |
2 |
|
.... |
a / 2r x |
r |
a |
/ 2r |
1 x |
r 1 |
|
.... |
a |
/ |
x |
n |
b / |
, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 n |
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
... |
|
|
|
... |
|
|
|
|
... |
|
|
|
|
|
... |
|
... |
|
|
1.18) |
|
|
|
|
|
|
|
|
|
|
|
a / rr x |
r |
a |
/ rr |
1 x |
r 1 |
|
|
.... |
a |
/ |
x |
n |
b / |
, . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r n |
|
r |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
b / |
1 |
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
b / |
|
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m. |
|
|
|
|
Система (1.18) эквивалентна исходной системе. |
|
|
|
|
|
||||||||||||||||||||||
Если хотя бы одно из чисел b/ |
1 |
,..., b/ |
|
отлично от нуля, то система |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
m |
|
|
|
|
|
|
|
|
|
|
||
(1.18) несовместна и вместе с ней несовместна исходная система. |
|
||||||||||||||||||||||||||
Если же b/ |
1 |
... b/ |
|
|
0 , то из укороченной системы получаем ба- |
||||||||||||||||||||||
|
|
r |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зисные неизвестные, перенеся в правые части укороченных уравнений свободные неизвестные.
27
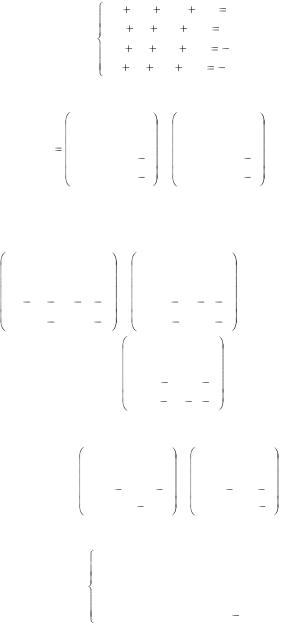
Пример 18. Решить систему
2x1 |
3x2 |
11x3 |
5x4 |
2, |
x1 |
x2 |
5x3 |
2x4 |
1, |
2x1 |
x2 |
3x3 |
2x4 |
3, |
x1 |
x2 |
3x3 |
4x4 |
3. |
Решение. Выпишем расширенную матрицу системы и произведем элементарные преобразования:
|
|
2 |
3 |
11 |
5 |
2 |
|
1 |
1 |
5 |
2 |
1 |
|
|
|
|
1 |
1 |
5 |
2 |
1 |
|
2 |
3 |
11 |
5 |
2 |
. |
|
A |
~ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
2 |
1 |
3 |
2 |
3 |
2 |
1 |
3 |
2 |
3 |
|
||||
|
|
1 |
1 |
3 |
4 |
3 |
|
1 |
1 |
3 |
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножим первую строку полученной матрицы на -2 и прибавим ко второй, затем – к третьей строке, а потом из последней строки вычтем первую.
Тогда имеем
|
|
1 |
1 |
5 |
2 |
1 |
|
1 |
1 |
5 |
2 |
1 |
|
|
|
0 |
1 |
1 |
1 |
0 |
~ |
0 |
1 |
1 |
1 |
0 |
~ |
A ~ |
|||||||||||||
|
|
0 |
1 |
7 |
2 |
5 |
|
0 |
0 |
6 |
1 |
5 |
|
|
|
0 |
0 |
2 |
2 |
4 |
|
0 |
0 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
5 |
2 |
1 |
~ |
0 |
1 |
1 |
1 |
0 . |
|
0 |
0 |
1 |
1 |
2 |
|
0 |
0 |
6 |
1 |
5 |
|
|
|
|
|
|
Умножим третью строку на –6 и прибавим ее к последней:
|
|
1 |
1 |
5 |
2 |
1 |
|
1 |
1 |
5 |
2 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 . |
A ~ |
~ |
|||||||||||
|
|
0 |
0 |
1 |
1 |
2 |
|
0 |
0 |
1 |
1 |
2 |
|
|
0 |
0 |
0 |
7 |
7 |
|
0 |
0 |
0 |
1 |
1 |
Полученная матрица является расширенной матрицей системы x1 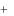 x2
x2 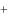 5x3
5x3 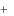 2x4
2x4 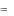 1,
1,
x2 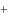 x3
x3 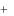 x4
x4 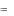 0, x3
0, x3  x4
x4 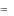 2, x4
2, x4 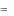 1.
1.
28
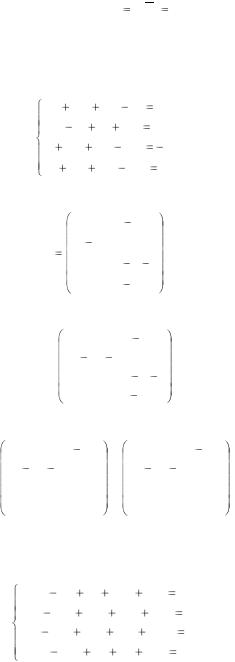
Эта система совместна, так как r( A) r( A) 4. Очевидно, решение
системы единственно, так как ранг матрицы равен числу неизвестных. Решим систему. Из последнего уравнения х4=-1. Поставляя х4 в
следующее уравнение, получим х3=1. Далее, подставляя х3 и х4 во второе уравнение, получим х2=0 и, наконец, х1=-2. Итак, х1= -2, х2=0, х3=1,х4=-1.
Пример 19. Исследовать совместность системы x1 2x2 3x3 x4 0,
x1 x2 x3 2x4 4,
x1 5x2 5x3 4x4 |
4, |
x1 8x2 7x3 7x4 6.
Решение. Произведем элементарные преобразования расширенной матрицы системы
|
|
1 |
2 |
3 |
1 |
0 |
|
|
1 |
1 |
1 |
2 |
4 . |
A |
||||||
|
|
1 |
5 |
5 |
4 |
4 |
|
|
1 |
8 |
7 |
7 |
6 |
|
|
|
|
|
|
|
Первую строку матрицы умножим на –1 и прибавим ее к остальным строкам. Получим
|
|
1 |
2 |
3 |
1 |
0 |
|
|
0 |
3 |
2 |
3 |
4 . |
A ~ |
||||||
|
|
0 |
3 |
2 |
3 |
4 |
|
|
0 |
6 |
4 |
6 |
6 |
Вторую строку полученной матрицы сложим с третьей строкой, а затем, умножив ее на 2, сложим с последней:
|
|
1 |
2 |
3 |
1 |
0 |
|
1 |
2 |
3 |
1 |
0 |
|
|
0 |
3 2 3 |
4 |
|
0 |
3 2 3 |
4 . |
||||
A ~ |
~ |
|||||||||||
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
14 |
|
|
0 |
0 |
0 |
0 |
14 |
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ранг матрицы системы равен двум, а ранг расширенной – трем. Следовательно, система несовместна.
Пример 20. Исследовать совместность и найти общее решение системы
2x1 |
x2 |
x3 |
2x4 |
3х5 |
2, |
6x1 |
3x2 |
2x3 |
4x4 |
5х5 |
3, |
6x1 |
3x2 |
4x3 |
8x4 |
13х5 |
9, |
4x1 |
2x2 |
x3 |
x4 |
2х5 |
1. |
29

Решение. Произведем элементарные преобразования расширенной матрицы системы
|
|
2 |
1 |
1 |
2 |
3 |
2 |
|
|
6 |
3 |
2 |
4 |
5 |
3 . |
А ~ |
|||||||
|
|
6 |
3 |
4 |
8 |
13 |
9 |
|
|
4 |
2 |
1 |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
Умножив первую строку матрицы на –3, сложим ее со второй и третьей строками, а, умножив на –2, сложим ее с четвертой строкой.
Тогда имеем
|
|
2 |
1 |
1 |
2 |
3 |
2 |
|
|
0 |
0 |
1 |
2 |
4 |
3 . |
А ~ |
|||||||
|
|
0 |
0 |
1 |
2 |
4 |
3 |
|
|
0 |
0 |
1 |
3 |
4 |
3 |
|
|
|
|
|
|
|
|
Сложим теперь вторую строку этой матрицы с третьей и вычтем ее
из четвертой: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
1 |
1 |
2 |
3 |
|
|
2 |
1 |
1 |
2 |
3 |
|
2 |
|
|
|
2 |
|
|
|||||||||||
|
|
|
0 |
0 |
1 2 |
4 |
3 |
|
0 |
0 |
1 |
2 |
4 |
|
3 . |
|
|
А ~ |
~ |
||||||||||||||
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как расширенная матрица системы А и матрица системы А содержат три ненулевых строки, то r( A) r( A) 3. Система совместна и,
так как ранг матрицы А меньше числа неизвестных системы, то система имеет множество решений.
Выберем в качестве базисного минора
|
1 |
1 |
2 |
|
M |
0 |
1 |
2 |
. Тогда неизвестные х2, х3, х4 – базисные, а х1 и х5 – |
|
0 |
0 |
1 |
|
|
|
|
|
|
свободные. Укороченная система имеет вид
x2 |
x3 |
2x4 |
2 2x1 3x5 , |
|
x3 |
2x4 |
3 4x5 , |
|
|
x4 |
0. |
Положим х1=с1, х5=с2. Тогда система примет вид
30
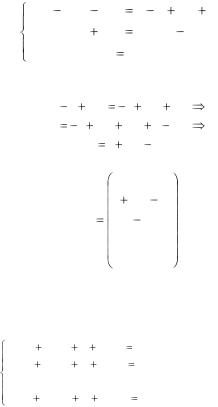
x2 |
x3 |
2x4 |
2 2с1 3с2 , |
|
x3 |
2x4 |
3 4с2 , |
|
|
x4 |
0. |
Так как х4=0, то из второго уравнения этой системы х3=3-4с2. Подставляя х4 и х3 в первое уравнение, получим
x2 |
3 4c2 |
2 2c1 3c2 |
x2 |
2 2c1 |
3c2 3 4c2 |
x2 1 2c1 c2 .
Следовательно, общее решение исходной системы имеет вид c1
1 2c1 c2
X (c1,c2 ) |
3 4c2 . |
0 c2
4.4. Однородные системы
Рассмотрим однородную систему линейных уравнений
a11x1 |
a12 x2 |
... |
a1n xn |
0, |
|
a21x1 |
a22 x2 |
... |
a2n xn |
0, |
(1.19) |
............................................. |
|
||||
am1x1 |
am2 x2 |
... |
amn xn |
0. |
|
Такая система всегда совместна, так как этой системе удовлетворяют значения х1=х2=…=хn=0. Это решение системы называют тривиальным.
Теорема. Для того чтобы однородная система линейных уравнений имела нетривиальное решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных n.
Доказательство. По теореме Кронекера-Капелли, если r=n, то система имеет единственное решение. А так как система (1.19) имеет всегда тривиальное решение, то в этом случае оно и единственно, то есть при r=n система имеет лишь тривиальное решение.
При r<n система является неопределенной, то есть имеет бесчисленное множество решений, в том числе и нетривиальное.
Замечание. Если m=n, то есть число уравнений совпадает с числом неизвестных, матрица системы является квадратной. условие r<n в этом случае означает, что определитель системы, то есть det А=0, что следует из определения ранга матрицы.
31
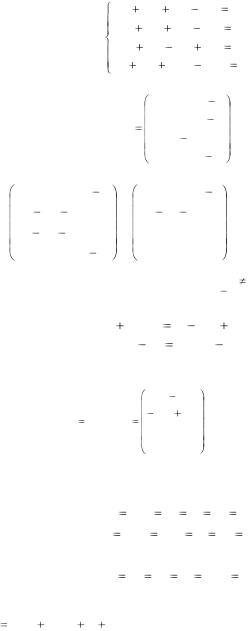
Пример 21. Решить систему
|
|
|
|
x1 |
2x2 |
|
4x3 |
3x4 |
0, |
|
|
|||
|
|
|
3x1 |
5x2 |
6x3 |
4x4 |
0, |
|
|
|||||
|
|
|
4x1 |
5x2 |
2x3 |
3x4 |
0, |
|
|
|||||
|
|
|
3x1 |
8x2 |
24х3 |
19x4 0. |
|
|||||||
Решение. Составим матрицу системы |
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
2 |
4 |
3 |
|
|
|
|
|
|
|
|
|
|
A |
3 |
5 |
6 |
4 |
|
|
|
|
|
|
|
|
|
|
4 |
5 |
2 |
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
8 |
24 |
19 |
|
|
|
||
и методом элементарных преобразований найдем ранг |
||||||||||||||
1 |
2 |
4 |
3 |
|
|
1 |
2 |
4 |
3 |
|
|
|
|
|
A ~ 0 |
1 |
6 |
5 |
~ |
0 |
1 |
6 |
5 |
. r=2. |
|
||||
0 |
3 |
18 |
15 |
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
3 |
18 |
15 |
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
Выберем в качестве базисного минор |
|
2 |
|
0. |
Тогда укороченная |
|||||||||
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
система имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x1 |
|
|
2x2 |
|
|
4x3 |
3x4 , |
|
|||
|
|
|
|
|
|
x2 |
6x3 |
5x4 . |
|
|
||||
Полагая х3=с1, |
х4=с2, находим |
х2=-6с1+5с2, а |
х1=-4с1+3с2+2(6с1- |
|||||||||||
5с2)=8с1-7с2. Общее решение системы |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
8c1 |
7c2 |
|
|
|
|
|
|
|
|
|
X |
X(c , c |
|
) |
6c1 |
5c2 |
. |
|
|
|
(1.20) |
||
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
c1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
c2
Назовем фундаментальной системой решений систему матрицстолбцов, полученную из общего решения при условии, что свободным неизвестным дают последовательно значения
с1 |
1,c2 |
c3 |
... |
cn |
0, |
с1 |
0,c2 |
1,c3 |
... |
cn |
0, |
.........................................
с1 c2 c3 ... 0,cn 1.
Матрицы-столбцы, то есть фундаментальную систему решений обозначают Е1, Е2, …, Еn. Общее решение будет представлено в виде
X C1E1 C2 E2 ... Cn En .
32
