
Курс лекций по высшей математике. 1 часть
.pdf
Доказательство. Допустим для определенности, что f (x) < 0 и докажем, что график выпуклый. Возьмем на графике функции произвольную точку М0 с абсциссой х0 (а, b) и проведем через точку М0 касательную. Для доказательства теоремы нужно показать, что для одной и той же абсциссы x ордината кривой меньше ординаты касательной. Это будет означать, что график функции находится ниже касательной. Уравнение касательной в точке М0 имеет вид У – f (х0) = f (х0).(х-х0). Здесь через У обозначена ордината касательной, соответствующая абсциссе x.
y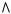
M 0
|
y f x |
f x0 |
Y |
0 a  x0 c c1 x b x
x0 c c1 x b x
Разность ординат графика и касательной при одной и той же абсциссе x равна
у У f (x)  f (x0 ) f (x0 ).(x x0 ) или
f (x0 ) f (x0 ).(x x0 ) или
у |
У |
f (x) f (x0 ) |
f (x0 )(x x0 ) |
Применяя к разности f(х) -f(х0) формулу Лагранжа, получаем |
|||
у |
У |
f (с).(x x0 ) |
f (x0 ).(x x0 ) (x x0 ).( f (с) f (x0 )), где |
cзаключено между х и х0.
Кразности f (с) f (x0 ) тоже применим формулу Лагранжа, по-
лучим |
|
|
|
у У |
(x x0 ) f (c1 )(c |
x0 ) , где c1 заключено между х0 и c, а, сле- |
|
довательно, |
между х0 и х. |
По условию |
f (x)< 0 в интервале (а; |
b),значит f |
(c1)< 0. Разности х- х0 и c – х0 |
одного знака, так как c за- |
|
ключено между х0 и х, значит (х- х0)(c – х0)> 0.
Поэтому у – У < 0 или у <У. Мы доказали, что для любой точки x интервала (а, b) ордината касательной больше ординаты графика, то есть график выпуклый. Аналогично доказывается, что при f (x) > 0 график
вогнутый.
123

Теорема 6. (достаточный признак существования точки перегиба). Если вторая производная f (x) непрерывной функции меняет знак при переходе аргумента через точку х0, то точка (х0; f(х0)) является точкой
перегиба графика функции. |
|
Доказательство. Пусть, например, |
f (х)< 0 в интервале (х0- ; х0) и |
f (x) > 0 в интервале (х0; х0+ ), где |
– положительное число. В этом |
случае график функции в интервале (х0–ε; х0) выпуклый, а в интервале (х0; х0+ε) – вогнутый. Следовательно, точка (х0; f(х0)) по определению является точкой перегиба.
Теорема 7. (необходимое условие существования точки перегиба). Пусть функция y = f(x) имеет в интервале (a, b) непрерывную вторую производную f''(x) и пусть точка х0 (a, b) является абсциссой точки перегиба графика данной функции. Тогда f''(x0) = 0.
Доказательство. Предположим противное: f''(x0) 0, например, для определенности f''(x0)>0. Тогда в силу непрерывности f''(x0)>0 в некоторой окрестности точки х0. Следовательно, в этой окрестности график вогнутый, но это противоречит тому, что х0 – абсцисса точки перегиба. Противоречие доказывает теорему.
Замечание. Могут встретиться случаи, когда в точке х0 вторая производная непрерывной функции не существует, однако точка является
абсциссой точки перегиба. Например, для функции у |
= 3 х5 у'' = |
||
|
|
|
|
10/(9 3 х ) у''(0) не существует. Очевидно, что у''<0 при х |
(-∞;0) и у''>0 |
||
при х (0;+∞), то есть точка (0; 0) является точкой перегиба.
Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками функции второго порядка. Как мы отметили, не все такие точки являются абсциссами точек перегиба.
п. 3. Асимптоты графика функции
Асимптотой графика функции у = f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении этой точки от начала координат.
Для нахождения вертикальных асимптот, то есть асимптот, параллельных оси OY, надо найти точки разрыва функции II рода. Если х0 –
такая точка, то хотя бы один из пределов |
lim f(x) или |
lim f(x) равен |
x |
x0 |
x x0 |
бесконечности. Это означает, что прямая х = х0 – вертикальная асимптота. Если функция не имеет точек разрыва II рода, то график функции не имеет вертикальных асимптот.
Пусть график функции y = f(x) имеет невертикальную асимптоту. Уравнение невертикальной прямой можно записать в виде y = kx+b.
124
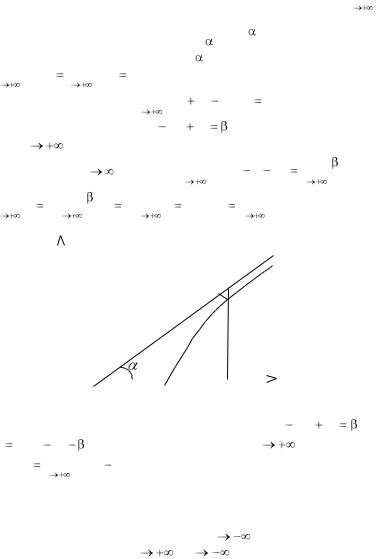
Пусть М(х,у) – текущая точка графика. Опустим из точки М перпенди-
куляр МN на асимптоту. Из определения асимптоты следует: |
lim |
MN = |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
0. Из ∆М1 |
MN получаем М1М = |
MN |
, где |
– угол между асимптотой |
|||||||||||||||||||||||||||||
cos |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
осью |
|
ОХ. |
|
Поскольку |
|
– |
|
величина |
постоянная, |
то |
||||||||||||||||||||||
lim M1M |
|
lim MN |
0 . Заметим, что М1М = РМ1-РМ = уасимпт.-уграфика |
||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
(kx+b)-f(x), |
поэтому |
lim |
((kx |
b) |
f (x)) |
|
0. Последнее |
равенство |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
означает, что функция |
f (x) |
(kx |
b) |
(x) |
является бесконечно малой |
||||||||||||||||||||||||||||
при x |
|
|
. Разделим обе части последнего равенства на х и перейдем |
||||||||||||||||||||||||||||||
к пределу при x |
|
, получим |
lim ( |
|
f (x) |
k |
|
|
|
b |
) |
lim |
|
(x) |
. Так как |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
x |
x |
|
x |
|
|
|
|||||
lim |
b |
|
0; lim |
|
(x) |
0; lim |
k |
k, то k |
lim |
|
f (x) |
|
|
|
|
|
|
||||||||||||||||
|
x |
|
x |
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||
x |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Определим |
теперь b. |
Так |
как |
|
f (x) |
(kx |
b) |
|
(x), |
то |
||||||||||||||||||||||
b |
f (x) |
|
kx |
(x). Переходя к пределу при x |
|
|
|
|
|
|
, получаем |
|
|||||||||||||||||||||
|
|
b |
lim ( f (x) |
kx) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если k или b не существуют, то график функции не имеет неверти- |
||||||||||||||||||||||||||||||||
кальной асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
В частном случае при k = 0 получается горизонтальная асимптота. |
||||||||||||||||||||||||||||||||
Аналогично находят асимптоты при x |
|
|
|
. График может иметь раз- |
|||||||||||||||||||||||||||||
личные асимптоты при x |
|
и x |
|
или иметь только одну из них. |
|||||||||||||||||||||||||||||
п. 4. План исследования функции и построение графика
Исследование функции удобно проводить по следующему плану.
1.Область определения функции.
2.Точки пересечения графика функции с осями координат.
125

3.Четность, нечетность функции.
4.Исследование функции на непрерывность. Вертикальные асим-
птоты.
5.Невертикальные асимптоты.
6.Интервалы монотонности. Экстремумы.
7.Интервалы выпуклости, вогнутости. Точки перегиба.
8. Дополнительные точки, lim f (x), lim f ' (x) (по мере необходи-
x |
x |
мости).
9. Построение графика.
Подчеркнем, что пункт 8 не является необходимым. его выполняют, если необходимо уточнить график.
Пример 1. Исследовать функцию |
y |
2x |
3 3 x2 |
и построить ее |
||||||||||||
график. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Область определения ( |
; |
). |
|
|
|
|
|
|
|
|
||||||
2. |
|
Пусть |
х=0, |
тогда |
у=0. |
Пусть |
у=0, |
|
тогда |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
. |
|
2х 3 3 х2 |
|
0;2х |
33 х2 ;8х3 |
27х2 ; х2 |
(8х |
27) |
0; х |
0 и |
х |
|||||||
|
8 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, (0;0) и ( 278 ;0) – точки пересечение графика с осями координат.
3. |
у(-х) = |
2х |
3 3 х2 |
– функция не является ни четной, ни не- |
|||
четной. |
|
|
|
|
|
|
|
4. |
Функция непрерывна во всей области определения. Вертикаль- |
||||||
ных асимптот нет. |
|
|
|
|
|
||
5. Невертикальные асимптоты |
|
|
|
||||
Найдем |
k |
и |
b, |
если |
они |
существуют. |
|
k |
lim |
f (x) |
|
lim |
2x 3 3 |
x2 |
|
|
lim (2 3 |
3 |
|
1 |
|
) |
2. |
|
|
|
|||
|
x |
x |
|
|
|
|
x |
|
|
|
|||||||||||
|
x |
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
b |
lim ( f (x) |
kx) |
|
lim (2x |
3 |
3 x2 |
2x) |
lim ( |
3 3 x2 ) |
, по- |
|||||||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
этому при |
x |
|
невертикальной асимптоты не существует. |
Анало- |
|||||||||||||||||
гично можно показать, что и при |
x |
невертикальных асимптот не |
|||||||||||||||||||
существует. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
6. Вычислим |
y' |
2 |
|
2 |
|
. Найдем критические точки: 2 |
2 |
|
0; |
|||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
x |
3 x |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
23 х |
2 |
|
|
|
|
|
|||||||||||||
0; 3 х |
1 |
0; х = 1 – критическая точка. Кроме того, y' не су- |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||
3 х |
|
|
|
|
|
|
|
|
|
|
|
||||||||
ществует при х = 0 – тоже критическая точка. Нанесем критические
126
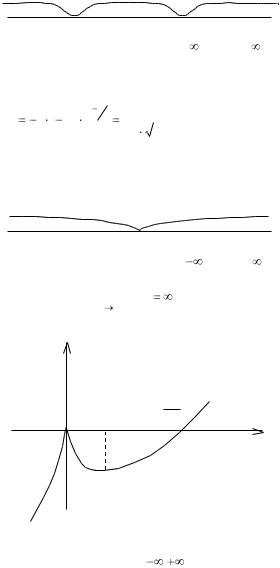
точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
+ |
- |
+ |
|
0 |
1 |
Таким образом, на интервалах (- |
;0) и (1;+ ) функция возрастает, |
|
на интервале (0;1) убывает.
уmax = f(0) = 0, ymin = f(1)= -1.
7. Вычислим
1 |
|
4 |
3 |
2 |
|
|
|
y' ' 2 ( |
|
) x |
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
3x 3 x |
|
|||
у'' не обращается в нуль ни при каком значении х и у'' не существует при х=0. х=0 – критическая точка второго порядка. Нанесем критическую точку на числовую прямую и определим знаки второй производной в образовавшихся интервалах.
+ |
+ |
0 |
|
Таким образом, на интервалах ( |
;0) и (0; ) график функции во- |
гнутый, точек перегиба нет.
8. Заметим, что lim f ' (x) , то есть в точке (0;0) график имеет
x 0
вертикальную касательную. y
27
8
0 |
1 |
2 |
3 |
x |
-1
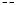
Пример 2. Исследовать функцию y = x-2arctg x и построить ее гра-
фик.
1. Область определения ( ; ) .
2. Пусть х = 0, тогда у = 0-2arctg 0 = 0.
Пусть y = 0, тогда х-2arctg x = 0; х = 2arctg x – решить такое уравнение точнo не удается.
127

Найдена точка (0;0) пересечения с осями координат. |
|
|||
3. у( x) |
x 2arctg( x) |
(x 2arctgx) |
y(x) |
функция не- |
четная.
4.Функция непрерывна во всей области определения. Вертикальных асимптот нет.
5.Невертикальные асимптоты.
y = kx+b
k |
lim |
|
f ( x ) |
lim |
|
x |
2acrtgx |
|
lim (1 |
2 |
|
arctgx |
) 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
x |
|
x |
|
|
|
x |
|
x |
|
|
|
|
x |
|
|
|
|
|||
b |
lim (x |
2arctgx |
|
x) |
|
2 lim |
arctgx |
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2 |
|
|
|
|
|
||
y |
x |
|
– асимптота при x |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
Выясним, есть ли асимптоты при х |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k |
lim |
|
f ( x ) |
lim |
|
x |
2acrtgx |
|
lim (1 |
|
2arctgx |
) 1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
x |
|
x |
|
|
|
x |
|
x |
|
|
|
x |
|
|
|
|
||||
b |
xlim (x |
2arctgx |
|
x) |
|
2 xlim |
arctgx |
|
|
2 ( |
|
|
) |
||||||||||
|
|
|
|
2 |
|||||||||||||||||||
y |
x |
|
– асимптота при x |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
6. y' 1 |
|
2 |
1 |
x2 |
2 x2 |
1 |
; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
x2 |
1 |
|
x2 |
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y' |
0; x2 |
1 |
|
0; x |
|
1 и х = 1 – критические точки. Нанесем кри- |
|||||||||||||||||
тические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
|
|
+ |
|
|
|
|
|
|
- |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
На интервалах ( |
|
; 1)и(1; |
) |
функция возрастает, на интервале |
|||||||||||||||||
(-1;1)– убывает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ymax |
f ( |
1) |
|
|
1 |
2arctg( |
1) |
1 |
2 ( |
|
|
) |
|
|
1 0,57 |
||||||
|
|
4 |
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ymin |
f (1) 1 |
2arctg1 1 |
2 |
|
1 |
|
|
|
0,57 |
|
|
||||||||||
4 |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. y'' |
|
|
4x |
|
; |
y'' = 0; 4х = 0; х = 0 – критическая точка второго |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
2 |
|||||||||||||||||
|
|
(1 |
x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
порядка. Нанесем ее на числовую прямую и определим знаки второй производной в образовавшихся интервалах.
128
|
|
|
|
- |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
На интервале ( |
;0) |
график выпуклый, на интервале (0; |
) |
– во- |
||||||||||||||
гнутый. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
х = 0 – абсцисса точки перегиба. |
|
|
|
|
|
|
|
|
|
|||||||||
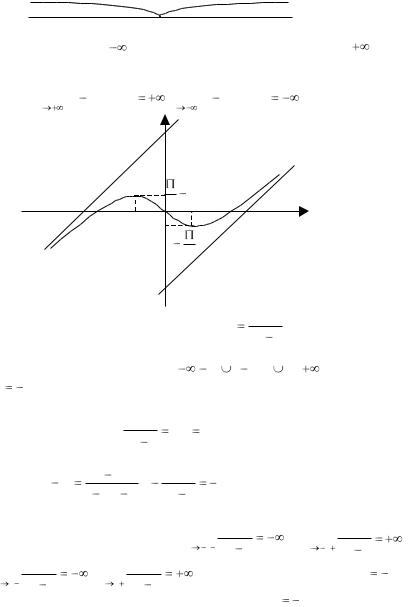
|
8. |
lim (x |
|
2arctgx) |
|
, lim (x |
2arctgx) |
|
. |
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=x+П |
|
|
|
-1 |
0 |
|
1 |
|
|
П |
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
y=x-П |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-П |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. |
Исследовать функцию |
y |
x |
|
и построить ее гра- |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
4 |
|
|
|
|
|
фик. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Область определения |
( |
; |
2 ) |
|
( 2;2 ) |
|
( 2; |
), |
так как при |
||||||||
x |
2 и х=2 в знаменателе получается нуль. |
|
|
|
|
|
|
|
|||||||||||
|
2. Пусть х=0, тогда у=0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пусть у=0, тогда |
x |
0,x |
0 |
|
|
|
|
|
|
|
|
|
||||||
|
x2 |
4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(0;0) – точка пересечения графика с осями координат. |
|
|
|
|||||||||||||||
|
3. |
y( x ) |
|
|
x |
|
= |
x |
|
y( x ) – функция нечетная. |
|
||||||||
|
|
( |
x )2 |
4 |
x2 |
4 |
|
||||||||||||
|
4. Функция имеет разрывы в точках х = -2 и х = 2, так как значения |
||||||||||||||||||
f(-2) |
и |
f(2) |
не |
определены. |
lim |
|
x |
|
|
; |
lim |
x |
|
; |
|||||
|
|
|
|
x2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x |
2 x2 |
4 |
|
|
x |
2 |
4 |
|
||
lim |
|
x |
|
; |
lim |
|
x |
|
. |
Это означает, |
что в точках x |
2 и |
|||||||
|
|
|
|
|
|
||||||||||||||
x 2 x2 |
4 |
|
|
x 2 x2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
х = 2 функция имеет разрывы II рода и прямые x |
2 и х = 2 являются |
||||||||||||||||||
вертикальными асимптотами. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
5. Найдем невертикальные асимптоты. |
|
|
|
|
|
|
|
|||||||||||
129
k lim |
f (x) |
lim |
1 |
|
0; |
|
x |
x2 |
4 |
||||
x |
x |
|
b lim ( f (x) |
kx) |
lim |
|
|
|
x |
lim |
|
1 |
|
|
|
|
0, следовательно, |
прямая |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x2 |
4 |
|
|
|
4 |
|
|
||||||||||||||||||||||
x |
|
|
|
x |
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
у=0 является горизонтальной асимптотой при х |
|
|
и х |
. |
|
|||||||||||||||||||||||||
6. |
|
|
Вычислим |
y' |
|
x2 |
4 |
|
x |
2x |
|
4 |
x2 |
0 |
при всех значени- |
|||||||||||||||
|
|
|
|
|
(x2 |
4)2 |
|
|
|
|
(x2 |
4)2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ях х, принадлежащих области определения функции. Точки х |
2 и х |
|||||||||||||||||||||||||||||
= 2 – критические, так как в них производная не существует. |
|
|
||||||||||||||||||||||||||||
|
|
|
- |
|
|
|
|
- |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На интервалах ( |
; 2), ( |
|
2;2), (2; |
|
) функция убывает. Экстрему- |
|||||||||||||||||||||||||
мов нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. |
Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y'' |
2x (x2 |
4)2 |
(4 x2 ) 2(x2 |
4) 2x |
|
2x(x2 |
|
|
4) 4x(4 x2) |
|||||||||||||||||||||
|
|
|
(x2 |
4)4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 4)3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2x3 |
8x 16x 4x3 |
|
2x3 |
24x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
( x2 |
4 )3 |
|
|
|
|
|
|
( x2 |
4 )3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y'' = 0; |
2x3 24x |
0 ; |
2x( x2 |
12 ) |
0; |
|
|
|
|
|
|
|
|
|
||||||||||||||||
х = 0; х 2; х = 2 – критические точки второго порядка. |
|
|
||||||||||||||||||||||||||||
|
|
|
- |
|
|
+ |
|
|
|
|
- |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
||||
|
|
|
|
|
–2 |
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
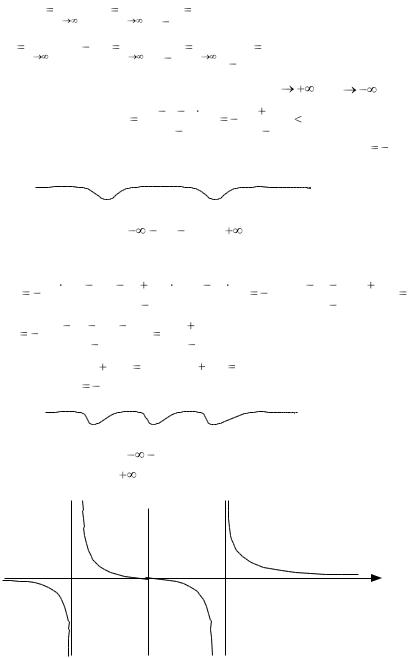
На интервалах ( |
; 2) и (0;2) график функции выпуклый, а на ин- |
|||||||||||||||||||||||||||||
тервалах (-2;0) и (2; |
) |
|
|
– вогнутый; х = 0 – абсцисса точки перегиба. |
||||||||||||||||||||||||||
y 
-2 |
0 |
2 |
x |
130
СОДЕРЖАНИЕ |
|
ГЛАВА I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ ........................ |
3 |
§ 1. ОПРЕДЕЛИТЕЛИ ............................................................................. |
3 |
§ 2. МАТРИЦЫ.................................................................................... |
12 |
§ 3. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ......... |
21 |
§ 4. ПРОИЗВОЛЬНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ .................. |
24 |
ГЛАВА II. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ |
|
ГЕОМЕТРИЯ ............................................................................................. |
34 |
§ 1. ВЕКТОРЫ. ОСНОВНЫЕ ПОНЯТИЯ................................................. |
34 |
§ 2. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ .................................... |
34 |
§ 3. ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ ....................................................... |
37 |
§ 4. КООРДИНАТЫ ВЕКТОРА............................................................... |
40 |
§ 5. НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА...................................... |
42 |
§ 6. ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ ............................... |
43 |
§ 7. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ...................................... |
45 |
§ 8. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ...................................... |
47 |
§ 9. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ .................................... |
49 |
§10. ПРЯМАЯ НА ПЛОСКОСТИ............................................................ |
52 |
§ 11. КРИВЫЕ ВТОРОГО ПОРЯДКА ...................................................... |
59 |
§ 12. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ ............................................ |
70 |
§ 13. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ .................................................. |
73 |
§ 14. ПРЯМАЯ В ПРОСТРАНСТВЕ ........................................................ |
76 |
§ 15. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ............... |
78 |
§ 16. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ........................................... |
81 |
ГЛАВА III. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ.... |
88 |
§ 1. ПРЕДЕЛ ФУНКЦИИ ....................................................................... |
88 |
§ 2. ОДНОСТОРОННИЕ ПРЕДЕЛЫ ........................................................ |
91 |
§ 3. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ......................... |
91 |
§ 4. ТЕОРЕМЫ О ПРЕДЕЛАХ ................................................................ |
93 |
§ 5. НЕКОТОРЫЕ ПРИЗНАКИ СУЩЕСТВОВАНИЯ ПРЕДЕЛА |
|
ФУНКЦИИ ................................................................................................... |
96 |
§ 6. ПЕРВЫЙ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ .......................... |
97 |
§ 7. НЕПРЕРЫВНОСТЬ ФУНКЦИИ ........................................................ |
99 |
ГЛАВА IV. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ |
|
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ................................................. |
105 |
§ 1. ПРОИЗВОДНАЯ........................................................................... |
105 |
§ 2. ДИФФЕРЕНЦИАЛ ФУНКЦИИ ....................................................... |
114 |
§ 3. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ.... |
116 |
§ 4. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ .... |
120 |
131
