Маршруты, цепи и циклы. Маршруты, цепи и циклы

Определение 6 (Маршрут). Маршрутом в графе G = <V,E; I> называется последовательность вершин и рёбер вида v₀,e₁,v₁,e₂, ..., v_n-1,e_n,v_n, где v_i  V, i  [0,n], e_i  E, (v_i-1,e_i), (v_i,e_i)  I, i  [1,n]. Вершины v₀, v_n называются связанными данным маршрутом (или просто связанными). Вершину v₀ называют началом, а v_n – концом маршрута. Если v₀ = v_n, то маршрут называют замкнутым. Число n называется длиной маршрута.

Определение 7 (Цепь, простая цепь, цикл). Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом. Маршрут, в котором все вершины попарно различны, называется простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.

Пример 2 (цепь). Маршрутa,{a,b},b,{b,c},c,{c,a},a,{a,d},dв первом графе из примера1является цепью, но не является простой цепью.

Замечание. Мы будем отождествлять циклы, являющиеся циклическими перестановками друг друга.

Графы часто используют для изображения различных отношений (например, иерархических отношений, т.е., на языке математики – отношений частичного порядка). Правда, для точного представления таких графов необходимо выразить понятие направления на графе. Мы не будем сейчас вводить новые понятия, а будем просто использовать расположение вершин на рисунках (одна выше или ниже другой).

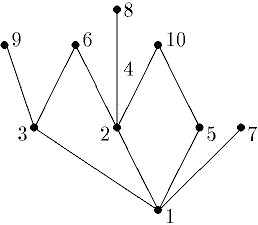
Пример 3 (граф отношения делимости). Построим граф, изображающее отношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}. Принцип такой: если от одного числа до другого есть цепь, ведущая вверх, тогда второе число делится на первое.

Связность графа

Определение 8 (Связность). Граф называется связным, если любая пара его вершин связана.

Определение 9 (Связные компоненты). Связными компонентами графа называются подграфы данного графа, вершины которых являются классами эквивалентности отношения свзанности в данном графе.

Определение 10 (Цикломатическое число). Цикломатическим числом графа называется число связных компонент графа плюс число рёбер минус число вершин.

Эйлеровы и гамильтоновы циклы

Определение 11 (Эйлеров цикл). Эйлеровым называется цикл, проходящий по каждому ребру графа ровно один раз. Граф, имеющий эйлеров цикл, тоже будем называть эйлеровым.

Пример 4 (эйлеров цикл). Построим эйлеров цикл для второго графа из задачи 1.1. Это h, {h,l}, l, {l,i}, i, {i,m}, m, {m,j}, j, {j,n}, n, {n,k}, k, {k,h}, h, {h,i}, i, {i,j}, j, {j,k}, k, {k,l}, l, {l,m}, m, {m,n}, n, {n,h}, h.

Теорема 1 (Критерий эйлеровости графа). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин – чётные числа.

Требование связности в теореме естественно – несвязный граф может быть эйлеровым только в том случае, если только одна связная компонента содержит рёбра.

Кроме понятия эйлерова цикла в задачах часто возникает необходимость нахождения цепи, проходящей по каждому ребру ровно один раз (снимается требование замкнутости. Такие цепи будем называть эйлеровыми цепями.

Определение 12 (Гамильтонов цикл). Гамильтоновым называется цикл, проходящий по каждой вершине графа ровно один раз.