Включение цепи на постоянное напряжение

Если схема содержит хотя бы 1 емкостный элемент, то решается относительно его.

НУ (нулевые)

Дифференциальное уравнение II порядка.

- характеристическое уравнение.

Но, можно было это уравнение не составлять, а воспользоваться тем же приемом.

- то же уравнение.

Дальше решение распадается на 3 варианта.

1) Если Д > 0: , то - действительное число, и - действительное число, и - так должно быть.

Тогда решение находят в виде

Нужно вспомогательное уравнение для определения и

При решаем эти два уравнения

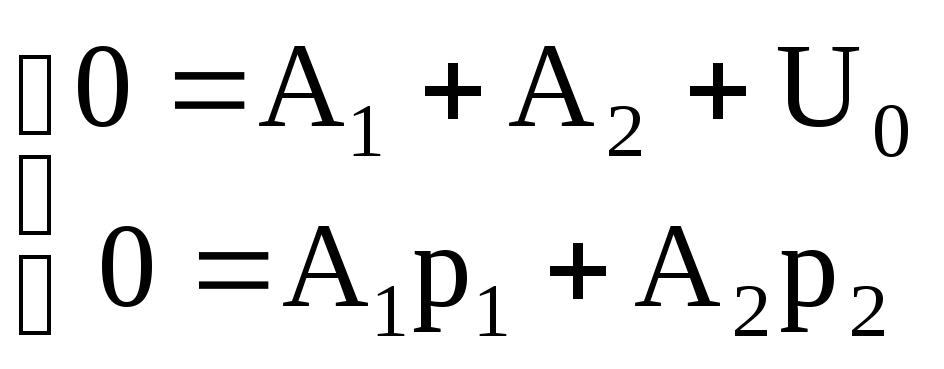
в другое уравнение

Отсюда

- можно найти

2) Д < 0

Тогда и - комплексные

,

Искать решение в виде

Из Н.Х. при опр. А и

Покажем, что решение из 1 случая здесь можно исп-ть.

должны =, но с разными знаками | =

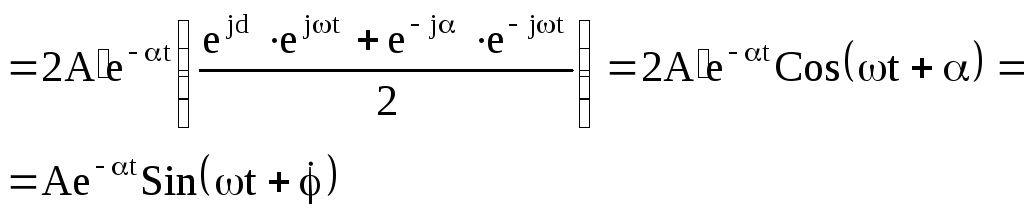
- найдем

3) Д = 0

Решение искать в виде:

переделать

При Н.У.

и найдем (или не найдем)

Для случаев 1, 2 и 3 построим временные графики n.n.

- вспомогательная кривая

- (мнимая часть корня)

- (действительная часть корня)

Т.к. и и элементы последовательно

Расчет n.n. классическим методом в цепях II порядка

Решим задачу анализа.

Решим, не составляя уравнений

Н.У.

Для нахождения корней характ. уравнения источник выбрасываем, ключ замыкаем.

Обрываем ветвь. Относительно точек 1,2 найдем

Найдем корни.

Пусть корни действит. и (<0)

Нашли и .

Нашли и .

Классический метод удобен для цепей 1, 2, ну и 3-го порядка. А если выше, то громоздок.

Расчет n.n. классическим методом при действии в цепи синусоидальных ЭДС

Пусть дана цепь:

Определить: i = ?

Н.У.

Общее решение то же самое

Корень тот же .

Будет

Процесс прошел, цепь:

Перейдем в временную область

При найти А

Построим график n.n.:

Пусть

Расчет n.n.в цепях с синусоидальными источниками классическим методом.

Д:

О:

Решение

Н.У.

чтобы найти постоянные интегрирования

Находим корень хар-го уравнения.

Для этого источники исключаем, ключ размыкаем.

Решение для тока 1 в виде:

А при

Для поиска 2 тока, та же формула:

Расчет n.n. классическим методом при некорректной коммутации.

Постоянное напряжение

Решим задачу анализа

Т.к. в Н.У.

- после замыкания должно

Обобщенный закон коммутации на индуктивности:

Дальше обычный классический метод.

при

Если

Строим график n.n.:

Решение дифференциальных уравнений методом Эйлера.

Возьмем дифференциальное уравнение

Приведем производную к конечным разностям

К – номер шага

h – шаг = const

К = 1

К = 2

Точность расчета определяется h – ом.

h связан с в данном случае

Если надо обеспечить 4 порядок малости такое n, чтобы совпадало 4 разряда.

В настоящее время получил наибольшее распространение в машинных расчетах метод Тунге – Кутта.