Глава шестая ряды ферье и их использование в анализе электрических цепей переменного несинусоидольного тока.

Основные понятия и определения:

Цепь линейная:

U – несинусоидальное напряжение

I – несинусоидальный ток

Если в электрической цепи несколько источников, то можно использовать метод наложения.

Условия:

1. функция должна быть периодической. В математике существует и непериодическая функция.

2. Если эта функция на периоде Т повторения имеет аналитическое выражение, то используется Интеграл Фурье.

3. Если она не имеет аналитического выражения в периоде повторения, то используют сумму интегралов (их приближенной значение).

1.Разложение периодической функции в ряд Фурье.

i=i₁+i₂+i₃+...+i_n, чем больше n – тем точнее решение.

Пусть дана векторная функция f(t) на периоде повторения t, в соответствии с этим её можно представить рядом Фурье.

A_k – коэффициент синусной гармоники ряда Фурье

Суммирование

Если известно аналитическое выражение, то берется интеграл или сумма n – интегралов. Можно бодобрать n – аналитических выражений.

Ряд Фурье для удобства расчета электрических цепей представляют в виде синусного ряда с начальным углом не равном 0 (косинусные).

Получим синусный ряд:

Обладает ли функция симметрией.

Симметричная относительно оси обсцисс.

Симметричная точка.

Синусоидальная гармоника присутствует.

Гдеk – четное число.

A_k=0, все косинусные гармоники отсутствуют k – любое.

Кривая, симметрична относительно оси абсцисс.

А общую строим по точкам, т.е. фбсциссу берем М, а значения разные ординат, т.е. складываются и строиться общий график.

2. Действующее и среднее значения несинусоидальных функций

Впеременном токе:

Вот и воспользуемся этими параметрами:

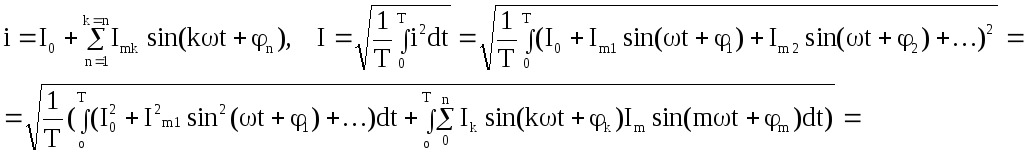
При раскрытии двух интегралов от произведения двух синусов, если их аргументы не равны, то второй интеграл равен 0. Поэтому:

Определение: действующим значением периодической функции называется квадратный корень из суммы квадратов удерживаемых гармоник ряда Фурье.

2. В переменном токе:

Определение:средним значением называют сумму средних значений гармоник ряда Фурье данной функции.

В электротехнике сравнивают качественные показатели при помощи коэффициентов:

3. Коэффициенты, оценивающие несинусоидальные функции.

1. Коэффициент формы:

Коэффициент формы оценивает на сколько искажена форма периодической функции по отношению к синусоидальной.

K_ф=1.11 для синусоидальной функции.

2. Коэффициент амплитуды К_А :

-коэффициент, показывоющий во сколько раз максимальное значение периодической функции превышает амплитуду основной гармоники.

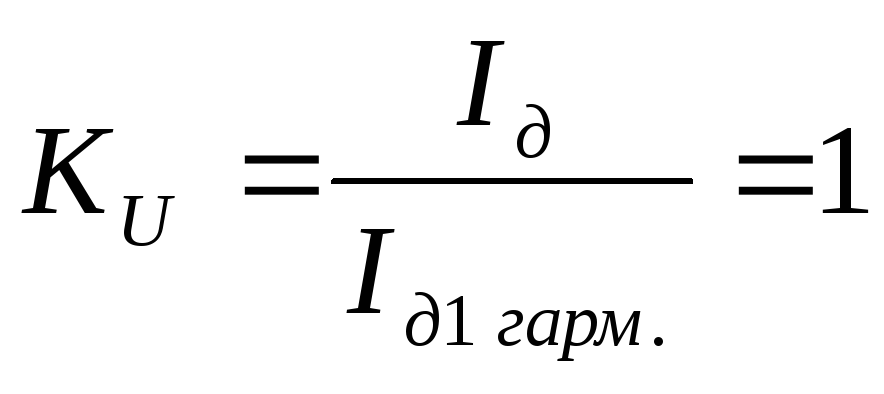3. Коэффициент искажений К_U :

-коэффициент, показывающий во сколько раз действующие значение, отличается от действительного значения первой гармоники.

К_U =1 (5%)-идеальный режим работы.

4. Коэффициент гармоник:

-коэффициент, показывающий отношение всех бесполезных гармоник к первой гармоники. Для напряжений 5% К_Г =0 - идеальный режим работы.

Можно определить долее точное значение:

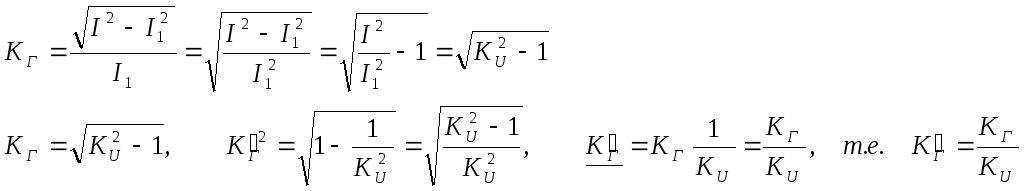
5. Коэффициент мощности:

Коэффициент, определяющий отношение суммарной активной мощности периодической функции к её полной мощности.

В линейной цепи существует понятие мощности.

А) если синусоидальная, то

Б) если цепь не синусоидальная, то

Если цепь работает в режиме не синусоидального тока, то нарушение (*) ликвидируется вводомT:

Где Т- реактивная мощности искажений, тогда:

Это и есть мощность в несинусоидальной цепи.

Часть шестая

Линейные электрические цепи с периодическими

несинусоидальными источниками