METOD

Следствия из формулы Бернулли:

5.Рn (n) = pn , Рn (0) = qn .

6.Pn(0) + Pn(1) + Pn(2) + … + Pn(n) = 1.

Предельная теорема Пуассона

Рассмотрим случай, когда вероятность р наступления некоторого события А достаточно малая величина. Например, рождение близнецов, достижение столетнего возраста, опечатка в книге и т. д. По формуле Бернулли Рn (k) = Cnk pk qn−k . В рассматриваемом случае n → ∞, а р → 0. Пусть величина λ

= np остается ограниченной: λ < const, k – фиксировано. При указанных

условиях справедлива теорема Пуассона Рn (k) ≈ λk e− λ . k!

Пользуясь теоремой Пуассона, мы можем при определенных условиях

данного выражения составлены таблицы, с их помощью можно для заданных k

элементарных исходов Ω – произвольное конечное множество на прямой, плоскости или n-мерном арифметическом пространстве. События – всевозможные измеримые подмножества А множества Ω. Вероятность события А - отношение лебеговой меры множества А и пространства элементарных

исходов: Р(А) = μ (А) .

μ (Ω)

Лебегова мера множества – это обобщение понятия длины отрезка, площади фигуры, объема тела. Например, для плоскости геометрическое определение вероятности будет выглядеть следующим образом.

Пусть D – некоторая конечная область плоскости. В эту область бросается точка, причем попадание ее в любую точку области D считается

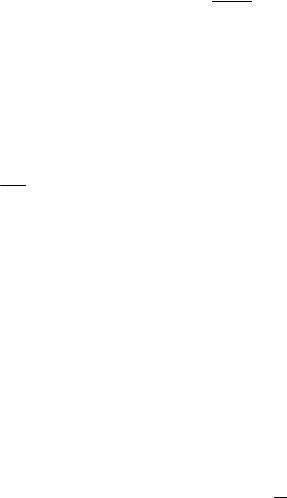
равновероятным. Тогда геометрической вероятностью попадания точки в любую область D1, лежащую в D, назовем отношение площади области D1 к

площади области D. P(D1) = S(DS(D)1 ) , где S(D1), S(D) – соответственно площади областей D1, D.

Статистическое определение вероятности. Пусть А – случайное событие по отношению к некоторому опыту. Предположим, что опыт произведен N раз и при этом событие А наступило в NA случаях. Отношение

ν = NNA называется частотой наступления события А в рассматриваемой

серии опыта. С увеличением числа опытов частота стабилизируется, приближается к некоторой постоянной р(А).

Определение. Статистической вероятностью случайного события р(А)

называют связанное с данным событием постоянное число, вокруг которого колеблется частота наступления этого события в длинных сериях опытов.

Количество информации

Количественная зависимость между вероятностью события (P) и количеством информации в сообщении о нем (I) выражается формулой:

I = log2( P1 ) = – log2P

Практические задания

Примеры решений

I тип. Общие понятия теории вероятности. Классическая вероятность. Геометрическая и статистическая вероятность

Задача. Подкидывается игральный кубик.

а) описать пространство элементарных исходов; б) указать невозможное и достоверное события для данного опыта;

в) найти исходы благоприятствующие появлению события А – выпало четное число;

г) найти вероятность наступления события А; д) найти событие, противоположное событию А и его вероятность. Решение.

а) В данном опыте возможны следующие исходы: «выпадение 1», «выпадение 2», «выпадение 3», «выпадение 4», «выпадение 5», «выпадение 6», т. е. пространство элементарных исходов – это множество {1, 2, 3, 4, 5, 6}.

б) Невозможным событием для данного опыта является, например, выпадение семерки. Достоверным событием является событие А – выпадение одного из шести очков: 1 или 2, или 3, или 4, или 5, или 6.

в) Событие А – выпало четное число, означает, что выпала 2 или 4, или 6, то есть исходами, благоприятствующими событию А, будут {2, 4, 6}.

г) Число благоприятствующих исходов для события А три, всего исходов 6, следовательно, по классическому определению вероятности

Р(А) = 63 = 12 .

д) Событие противоположное событию А есть событие А – не выпало четное число, т. е. выпало нечетное число. Число благоприятствующих исходов для события А три {1, 3, 5}, всего исходов 6, итак по классическому

определению вероятности Р( А) = 63 = 12 .

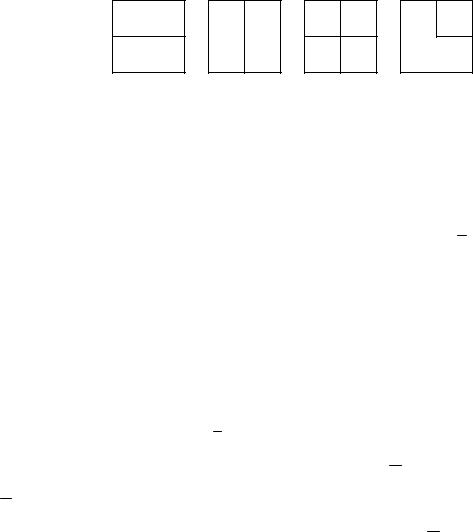
Задача. Опыт заключается в том, что на квадратный лист случайным образом кидается шарик. Пусть А – шарик попадает в верхнюю часть листа, В – шарик попадает в правую часть листа.

Найти события А + В и А • В. Решение.

Событие А + В – шарик попадает в верхнюю или в правую часть листа. Событие А • В – шарик попадает в правую верхнюю четверть листа. Графически это можно изобразить следующим образом (см. рис.):

Задача. На 33 карточках написаны буквы русского алфавита. Какова вероятность, что на случайно извлеченной карточке будет гласная буква (А), согласная (В), ни гласная и ни согласная буква (С)? Какова вероятность, что на случайно извлеченной карточке не будет гласная буква ( А),

Решение.

Общее число исходов 33. Исходов благоприятствующих событию А десять (все гласные буквы), событию В – двадцать один (все согласные буквы), событию С – два (твердый и мягкий знаки). Итак, по классическому определению вероятности: Р(А) = 10/33, Р(В) = 21/33, Р(С) = 2/33.

Вероятность события А – на карточке не будет гласной буквы, можно найти, опираясь на свойство вероятности Р(А) + Р( А) = 1, то есть

Р( А) = 1 – Р(А) = 1 – 10/33 = 23/33.

Ответ: Р(А) = 10/33, Р(В) = 21/33, Р(С) = 2/33, Р( А) = 23/33.

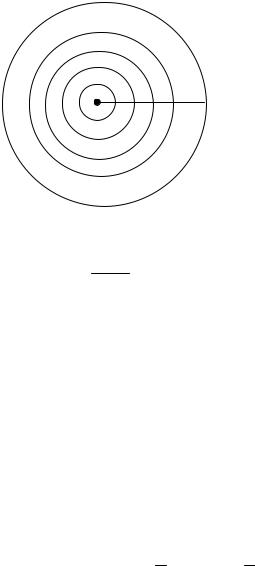
Задача. Радиус мишени 10 см. Какова вероятность, что стрелок попадет в область от 10 до 7, если круги мишени отстоят друг от друга на 1 см.?

Представим события С, D, E, F через события А и В:

Событие С – оба вытянут счастливые билеты, состоит из событий А – первый студент вытянет счастливый билет и В – второй студент вытянет счастливый билет, т. е. С = А • В.

Событие D – один из студентов вытянет счастливый билет состоит из следующих событий: А – первый студент вытянет счастливый билет и В–

второй студент не вытянет счастливый билет или А – второй студент вытянет счастливый билет и В – первый студент не вытянет счастливый билет. То есть

D = А • В + А • В.

Событие Е – ни один не вытянет счастливый билет, состоит из событий А

– первый студент не вытянет счастливый билет и В – второй студент не

вытянет счастливый билет, т. е. E = А В.

Событие F – хотя бы один не вытянет счастливый билет, состоит из события E – неверно, что ни один не вытянет счастливый билет, т. е. F = E =

А В.

События А и В независимы, следовательно и события В, А независимы. При подсчете вероятности событий можно применять правило произведения независимых событий.

Р(С) = Р(А • В) = Р(А) • Р(В) = 0,45 • 0,55 = 0,2475.

Р(D) = Р(А • В + А • В) = Р(А • В) + Р( А • В) = Р(А) • Р( В) + Р( А) • Р(В) = Р(А) • (1 – Р(В)) + (1 – Р(А))• Р(В)= 0,45 • 0,45 + 0,55 • 0,55 = 0,2025 + 0,3025 = 0,505 (События А • В и А • В несовместны).

Р(Е) = Р( А • В) = Р( А) • Р( В) = (1 – Р(В)) • (1 – Р(А)) = 0,55 • 0,45 = 0,2475.

Р(F) = P( E ) = 1 – P(E) = 1 – 0,2475 = 0, 7525.

Задача. Из 29 билетов 13 – счастливые. Какова вероятность того, что первый студент вытянет счастливый билет, а второй следом за ним несчастливый?

Решение.

Пусть В – первый студент вытянул счастливый билет, А – второй студент вытянул несчастливый билет. Тогда событие А•В – первый студент вытянул счастливый билет, а второй – несчастливый. А и В – зависимые события. Р(В) =

1329 , при условии, что первый билет был счастливый, вероятность вытянуть

произведения зависимых событий Р(АВ) = Р(А/В)Р(В) = 74 1329 = 20352 .

Задача. В аудитории занимались 3 группы. В первой группе 5 отличников, во второй 7, в третьей 3.

а) Какова вероятность, что случайно оставленная зачетка принадлежит отличнику, если в первой группе 22 студента, во второй – 20, в третьей – 25?

б) Найти вероятность того, что потерянная зачетка отличника принадлежит студенту первой группы? Второй группы? Третьей группы?

Решение.

а) Очевидно, что вероятность искомого события будет изменяться в зависимости от того, студент какой группы потерял зачетку.

Пусть А – оставленная зачетка принадлежит отличнику, В1 – зачетка принадлежит студенту первой группы, В2 – зачетка принадлежит студенту второй группы, В3 – зачетка принадлежит студенту третьей группы.

В1, В2, В3 – независимые события. События А/В1, А/В2, А/В3 означают, что зачетка принадлежит отличнику, при условии, что зачетка принадлежит студенту первой, второй, третьей группы соответственно. Следовательно, событие А = А · В1 + А · В2 + А · В3, что означает, что событие А наступит в случае, если зачетка принадлежит студенту первой группы и зачетка отличника, или если зачетка принадлежит студенту второй группы и зачетка отличника, или если зачетка принадлежит студенту третьей группы и зачетка отличника.

Поэтому Р(А) = Р(В1)Р(А/В1) + Р(В2)Р(А/В2) + Р(В3)Р(А/В3), так как произведение событий А и Вi находится по формуле условной вероятности.

Р(В1) = 6722 , Р(В2) = 6720 , Р(В3) = 6725 . Р(А/В1) = 225 ; Р(А/В2) = 207 ; Р(А/В3)

= 253 .

потерянная зачетка отличника принадлежит студенту второй группы и третьей группы:

III тип. Комбинаторные задачи на вероятность

Задача. Набирая номер телефона, абонент забыл первые 3 цифры. Какова вероятность правильного набора абонентом цифр наугад?

Решение.

Данную задачу можно разбить на 2 части:

Определить, сколькими способами можно составить трехзначное число (первые 3 цифры телефона); Определить вероятность набора абонентом верного номера наугад.

Трехзначное число состоит из трех цифр: abc . Первую цифру – число тысячных (множество a), можно выбрать из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9, т. е. множество

а = {1, 2, 3, 4, 5, 6, 7, 8, 9}, b = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, c = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Таким образом, задачу можно переформулировать: сколькими способами (N) из элементов множеств a, b, c можно составить тройку упорядоченных элементов? Согласно правилу произведения N = 9 · 10 · 10= 900.

Из 900 номеров только один является верным, следовательно вероятность набора верного номера наугад Р(А)=1/900.

Ответ: 1/900.

Задача. Написано слово МИР! Буквы (символы) записали на отдельных карточках и перемешали. Какова вероятность того, что наудачу извлеченные по порядку буквы снова составят слово МИР!

Решение.

Всего имеется 4 карточки: М, И, Р, !. Из них нужно составить определенное слово из 4 букв, т.е. нужно найти количество перестановок 4 символов по 4 местам. Р4 = 4! = 24.

При данных перестановках только один вариант расставления имеющихся символов подойдет по условию. Следовательно, вероятность наудачу составить нужное слово Р(А)= 1/24.

Ответ: 1/24.

Задача. В урне лежат 8 занумерованных шаров. Наугад берут 4 шара. Какова вероятность того, что 3 шара окажутся с нечетными номерами?