Лекция 12.

Термодинамические функции состояния. Функции распределения. Классическая и квантовая статистики. Статистические распределения. (2 часа)

12.1. Микроскопические параметры. Вероятность и флюктуации. Распределение молекул /частиц/ по абсолютным значениям скорости. Распределение Максвелла.

12.2. Средняя кинетическая энергия частицы. Скорости теплового движения частиц.

12.3. Распределение Больцмана.

12.4. Теплоемкость многоатомных газов. Ограниченность классической теории теплоемкостей.

12.5. Статистический смысл термодинамических потенциалов и температуры. Роль свободной энергии.

12.6. Распределение Гиббса для системы с переменным числом частиц.

12.7. Принцип Нернста и его следствия.

Демонстрации:

1. Распределение молекул по скоростям.

2. Атмосферное давление.

Распределение молекул по скоростям.

Распределение Максвелла

Основные понятия теории вероятностей

Впервые решил задачу распределения молекул по скоростям Максвелл в 1859 году.

Пусть мы имеем ансамбль из N молекул

Параметр Х - принимает значения Х₁;X₂;X_3.........X_i........

которые выпали соответственно N₁,N₂,N₃ ........N_i ......раз..

N_i -- число молекул у которых параметр Х принимает значение Х_i , тогда отношение

P_i = N_i / N

вероятность того что параметр Х имеет значение X_i

Пример : ИГРАЛЬНАЯ КОСТЬ

Кость имеет 6 граней, она должна быть однородной. Будем бросать кость 6 000 раз. События Х_{i -выпадание той или иной цифры от 1 до 6}

_{Пусть 1} выпадает 999 раз P₁=999/6000=1/6

2- выпадает 1001 раз P₂=1001/6000= 1/6

3- выпадает 998 раз P₃=998/6000 = 1/6

4- выпадает 1003 раз P₄=1003/6000= 1/6

5- выпадает 996 раз P5=996/'6000 = 1/6

6- выпадает 1000 раз P6=1000/6000 =1/6

----------------------------------

Сумма общего числа испытаний равняется 6 000, а вероятность каждого из событий равна 1/6

Если же за N возьмем не 6 000 а 60 000, то вероятность P_{i каждого из событий еще ближе к 1/6.}

СВЯЗЬ СРЕДНЕГО ЗНАЧЕНИЯ С ВЕРОЯТНОСТЬЮ

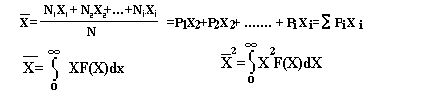
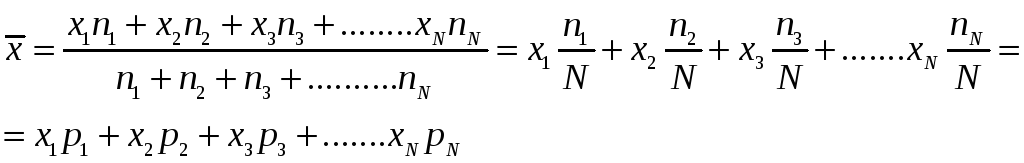
Если же случайные события или параметр Х изменяется не дискретно а непрерывно, то

dP(x)=F( X )dx

представляет собой вероятность нахождения параметра Х в интервале от Х до Х+dX

F(X)-- плотность вероятности или функция распределения вероятности .

Тогда число молекул, у которых значение параметра Х принадлежат интервалу от X до dX определяется соотношением:

dN=NdP(x)=NF(х)dх

РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА

Скорость молекулы тоже случайная величина , тогда число молекул ( dNv ) модуль

скорости которых лежит в интервале от V до dV определяется соотношением:

dNv=NdP : dPv=F(V)dV : dN=NF(V)dV

где F(V) -- функция распределения вероятности значения скорости

Основное уравнение молекулярно-кинетической теории приводит к выводу о том, что средний квадрат скорости молекул зависит от температуры газа и определяется формулой

,

которую можно также представить в виде

.

Величину - называют среднеквадратичной скоростью. Будем обозначать ее

.

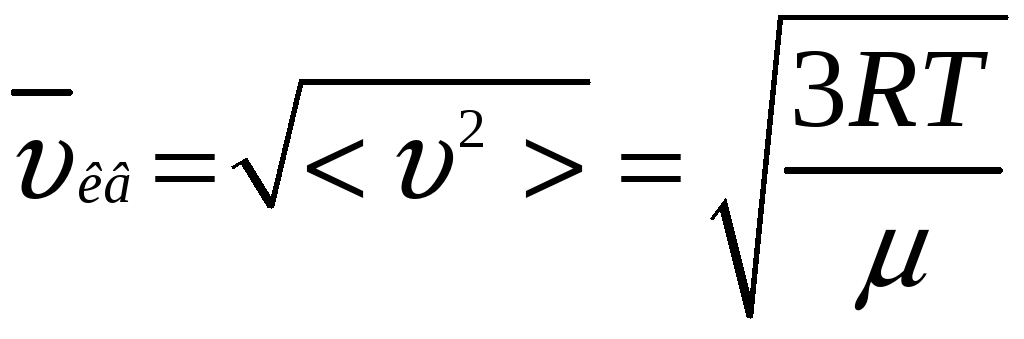Расчеты показывают, что величина среднеквадратичной скорости молекул азота (воздуха) при нормальных условиях равна

Очевидно, что при хаотическом движении молекулы газа имеют не одинаковые скорости. Их величина с течением времени непрерывно изменяется. Скорости молекул могут принимать любые значения в интервале от 0 и до бесконечности. Однако средние характеристики этого движения имеют вполне определенные численные значения, зависящие только от температуры газа. Впервые закон распределения скоростей молекул был получен Дж. Максвеллом в 1859 году. В соответствии с этим законом доля молекул, скорости которых принадлежат заданному интервалу скоростей от до , определяется соотношением

З десь - число всех молекул в сосуде, - число молекул, скорости которых принадлежат заданному интервалу скорости (от до ), - масса молекулы, - абсолютная температура, - постоянная Больцмана.

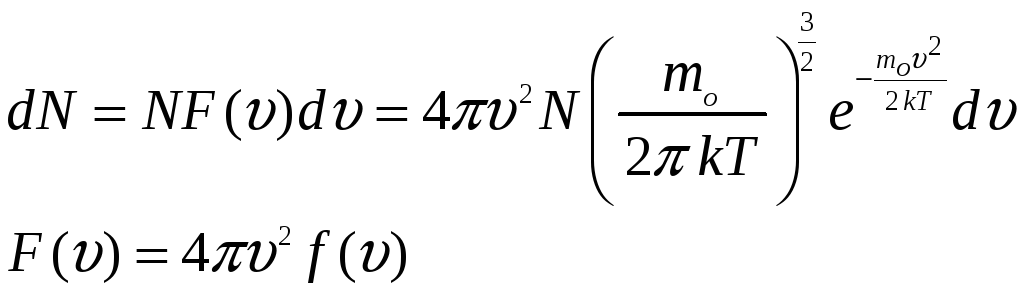
- плотность вероятности

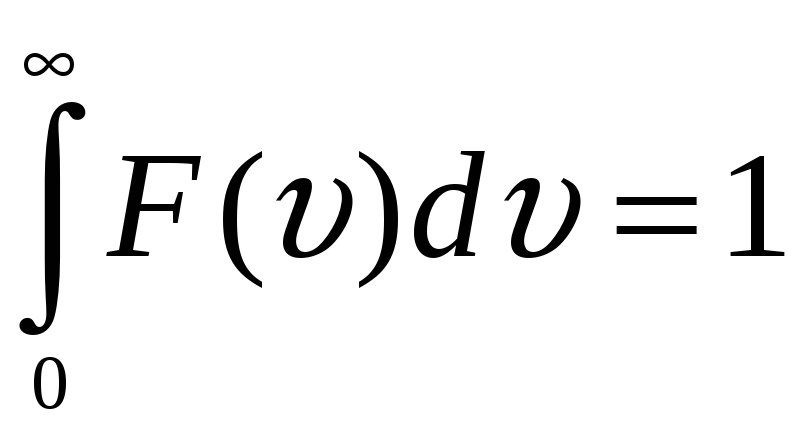
Приведенное соотношение называют законом распределением Максвелла по скоростям молекул. Как оказалось распределение Максвелла справедливо не только для газов. По закону Максвелла распределены скорости молекул жидкостей и твердых тел. Распределение Максвелла удобно проанализировать с помощью диаграммы, на которой представлена зависимость функции распределения от скорости . Функция распределения Максвелла имеет вид:

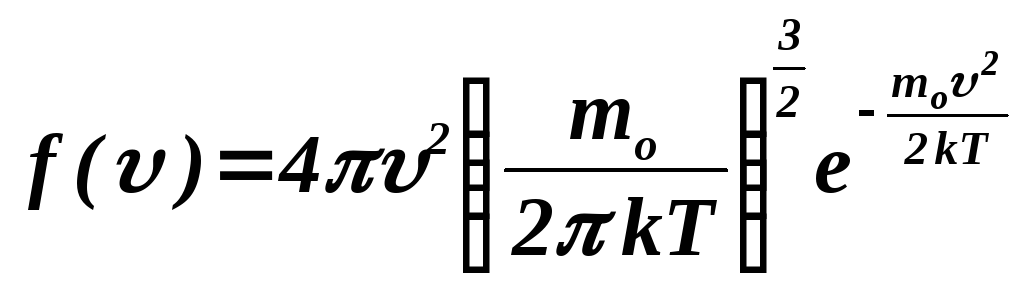
На приведенной диаграмме площадь узкой полоски численно равна доле молекул, скорости которых принадлежат заданному интервалу скоростей, а площадь под кривой численно равна единице, т.к. характеризует молекулы, скорости которых принимают любые значения от 0 до .

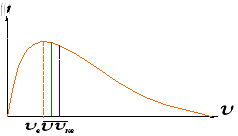Функция распределения Максвелла имеет максимум. Скорость, соответствующую максимуму функции распределения называют наиболее вероятной скоростью. Величину наиболее вероятной скорости можно определить из условия экстремума функции распределения. Дифференцируя функцию распределения и приравнивая полученный результат нулю, получим:

.

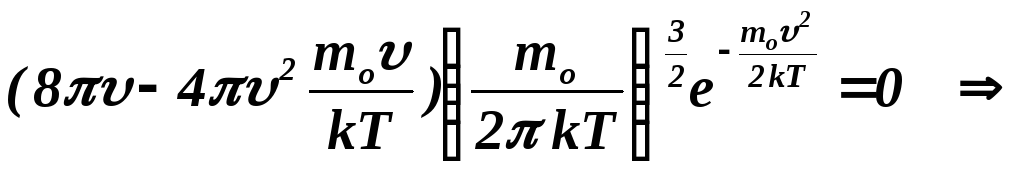
Как видим, наиболее вероятная скорость меньше среднеквадратичной скорости. С помощью распределения Максвелла можно рассчитать также среднюю скорость молекул газа. Ее величина определяется формулой

.

Более удобными для расчетов среднеквадратичной, наиболее вероятной и средней скоростей молекул формулы приведены ниже:

Отношение скорости молекулы к наиболее вероятной скорости ансамбля молекул называют приведенной или относительной скоростью молекулы

Распределение Максвелла для приведенной скорости:

Сколько молекул в моле имеют скорости отличающиеся от наиболее вероятной не более чем на 0.1

Распределение Максвелла получило экспериментальное

подтверждение в 1920 г. в опытах Штерна.

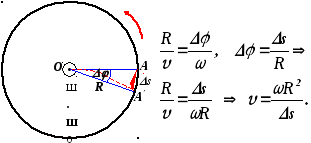
Опыты Штерна сводились к следующему. Два коаксиальных цилиндра приводились в быстрое вращение. На внутренней поверхности большого цилиндра осаждались пары серебра, которые в виде узкого пучка выходили из узкой щели малого цилиндра. Внутри большого цилиндра поддерживался глубокий вакуум. Вдоль оси малого цилиндра располагалась тонкая нить, покрытая тонким слоем серебра и нагреваемая электрическим током. В соответствии с представлениями молекулярно-кинетической теории скорости атомов серебра распределены по закону Максвелла. Величину скорости атомов серебра можно определить по формуле:

,

в которой - радиус большого цилиндра, - угловая скорость вращения цилиндров, - величина, характеризующая положение осажденного атома серебра.

Прямые измерения указанных величин и анализ плотности осажденных атомов серебра приводят к выводу о том, что Максвелловский закон распределения по скоростям полностью подтверждается данным экспериментом.