§7. Одновременность событий. Синхронизация часов

Напомним, что под системой отсчета подразумевается тело отсчета, с которым связаны система координат и ряд неподвижных одинаковых часов, синхронизированных между собой. Часами будем считать любой прибор, в котором используется тот или иной периодический процесс.

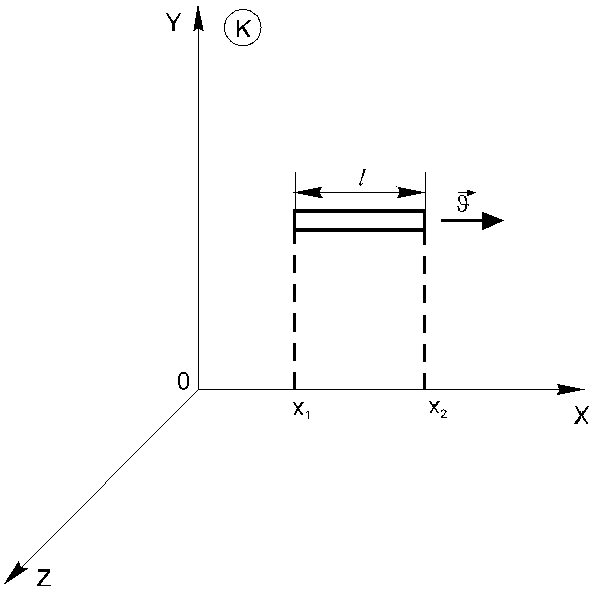
При проведении различных физических измерений широко пользуются понятием одновременности двух или нескольких событий. Например, для определения длины стержня, расположенного вдоль осиX системы отсчета К и движущегося относительно этой системы (рис. 7.1), необходимо одновременно, то есть в один и тот же момент времени , зафиксировать значения координатиконцов стержня:

. (7.1)

Для этого в каждой системе отсчета должно быть множество часов, находящихся в различных точках пространства. Все эти часы должны идти согласованно, синхронно - их показания в каждый момент времени должны быть одинаковыми.

Рис. 7.1

Синхронизировать часы, помещенные в различные точки системы отсчета, можно только с помощью каких-либо сигналов. Наиболее быстрые сигналы, пригодные для этой цели, - это световые или радиосигналы, которые распространяются с известной скоростью С. Выбор световых сигналов обусловлен еще и тем, что их скорость не зависит от направления в пространстве, а также одинакова во всех инерциальных системах отсчета.

Синхронизацию часов можно произвести следующим образом. Допустим что, из начала системы координат точки 0 по радио в момент времени передается радиосигнал. В момент, когда этот сигнал достигнет часов, находящихся от точки0 на известном расстоянии S, их устанавливают так, чтобы они показывали время , то есть с учетом времени распространения сигнала. В результате такой операции все часы данной системы отсчета будут синхронизированы в каждый момент времени.

§8. Преобразование Лоренца

Тот факт, что второй постулат специальной теории относительности несовместим с классическим законом сложения скоростей, а следовательно, и с преобразованиями Галилея, приводит к необходимости отказаться от этих преобразований. Возникает задача нахождения истинных формул преобразований при переходе от одной инерциальной системы отсчета к другой, то есть формул, связывающих координаты и время одного и того же события в двух инерциальных системах отсчета.

Новые преобразования были выведены Эйнштейном на основе сформулированных им постулатов. Формально они совпали с преобразованиями, найденными ранее Лоренцем в связи с попытками объяснить неудачу опыта Майкельсона. Но только Эйнштейн вскрыл их глубокий смысл.

Рассмотрим две инерциальный системы отсчета К и К' (рис. 5.1). Как и прежде, система К' движется относительно системы К в направлении оси X с постоянной скоростью . Установим в разных точках обеих систем отсчета одинаковые часы и синхронизируем их: отдельно часы системыК и отдельно часы системы К'. За начало отсчета времени возьмем в обеих системах момент (), когда начала координат (точки0 и 0') совпадают.

Так как система К' движется относительно системы К равномерно, связь между координатами идолжна по-прежнему, как и в преобразованиях Галилея, линейно зависеть от времени, то есть

, (8.1)

где - некоторый коэффициент.

Аналогичное выражение можно записать для обратного перехода от системы К к системе К':

. (8.2)

Для определения коэффициента предположим, что в начальный момент времени (), когда точки0 и 0' совпадали, из точки 0 в направлении оси X был послан световой сигнал, который через время , измеренное в системеК, достиг точки А с координатой . В системеК' эта точка имела координату , где- время, измеренное в системеК'. Заметим, что скорость С в силу второго постулата одна и та же.

Подставив координаты ив выражения (8.1) и (8.2), получим

,

(8.3)

.

Перемножив правые и левые части этих равенств и произведя сокращение на , получим

,

откуда

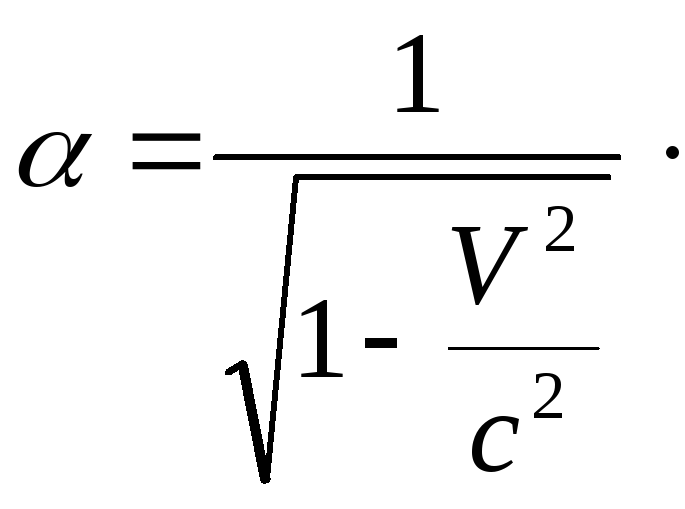(8.4)

Таким образом, связь между координатами иимеет вид:

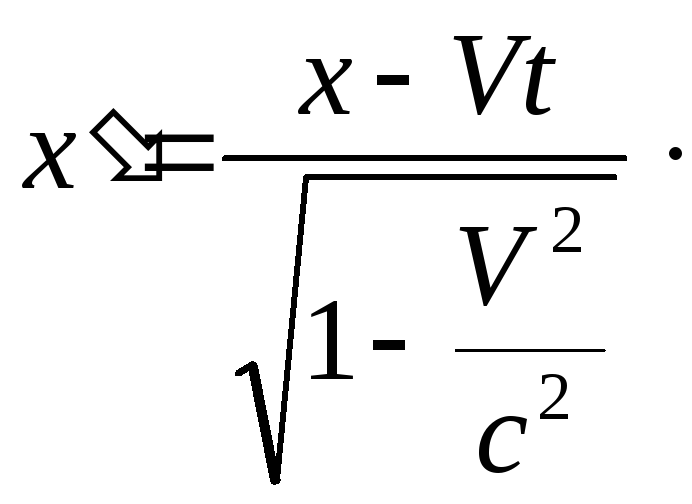(8.5)

Для нахождения связи между ипроделаем следующее. Исключив из выражений (8.1) и (8.2) величинуи решив их после этого относительно, получим с учетом выражения (8.4):

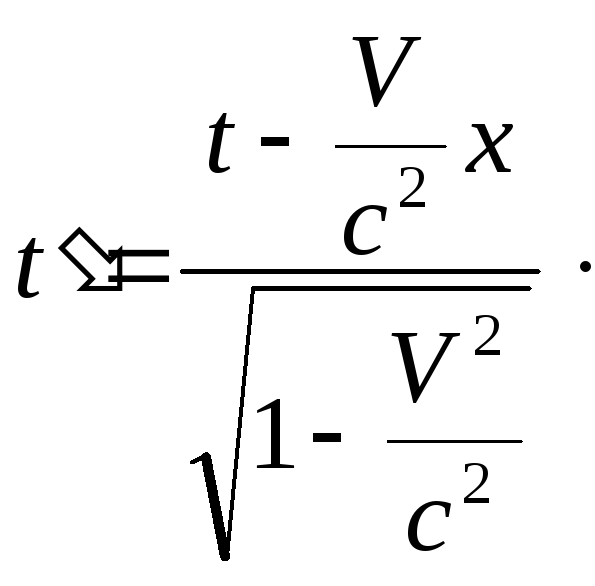(8.6)

Координаты иипри рассматриваемом движении системК и К' остаются равными друг другу.

Таким образом, преобразования для координат и времени, получившие название преобразований Лоренца, имеют вид:

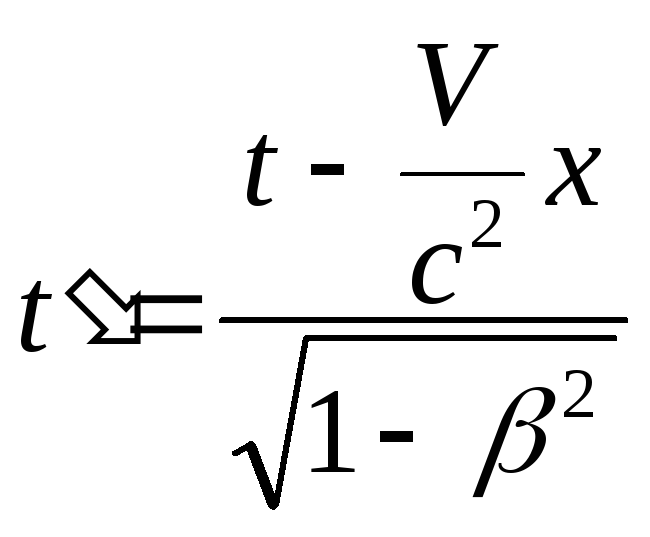^, ,,^, (8.7)

где

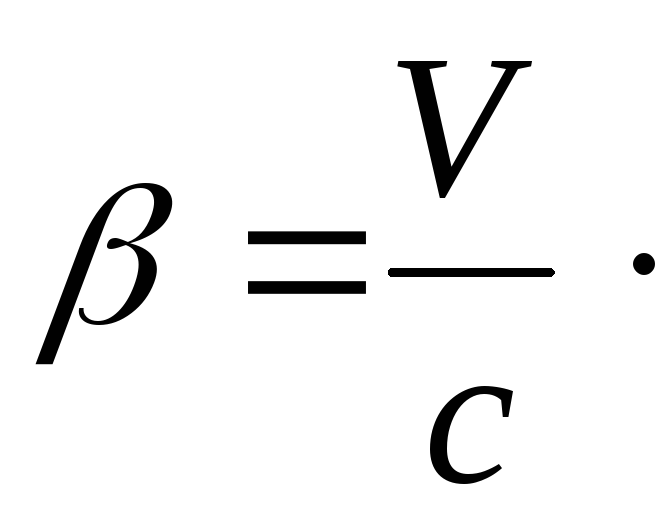
Обратные преобразования в силу равноправности всех инерциальных систем отсчета должны иметь аналогичный вид, но с учетом изменения знака скорости V:

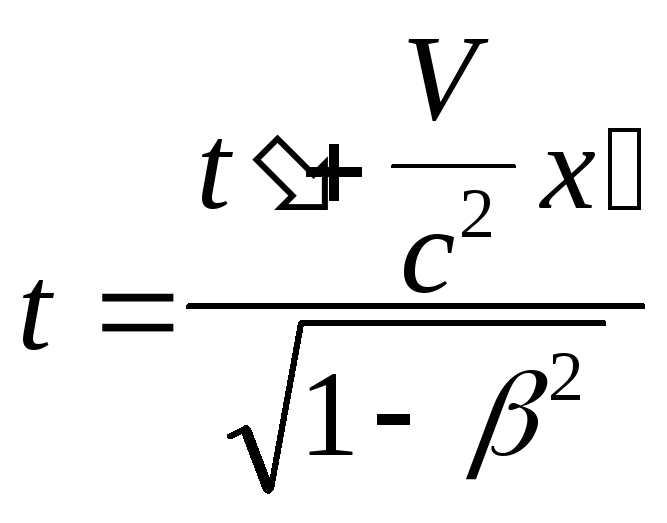^, ,,^. (8.8)

Анализ формул преобразований Лоренца позволяет сделать ряд важных выводов.

Во-первых, особенностью преобразований Лоренца является то, что при они переходят в преобразования Галилея (5.1). Это означает, что теория относительности не отвергает преобразования Галилея, а включает их в истинные преобразования как частный случай, справедливый при.

Во-вторых, из преобразований Лоренца следует, что при подкоренные выражения становятся отрицательными и формулы теряют физический смысл. Это означает, что движение тел со скоростью, большей скорости света в вакууме, невозможно.

В-третьих, в формулы преобразования времени входит пространственная координата, что отражает неразрывную связь пространства и времени.