АНАЛИЗ АКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ МЕТОДА ФИЛЬТРАЦИИ КАЛМАНА

И.П. Гуров, П.Г. Жиганов, А.М. Озерский

Рассматриваются особенности динамической обработки стохастических сигналов с использованием дискретных фильтров Калмана первого и второго порядка. Показана необходимость наличия адекватной априорной информации для эффективного анализа акустических сигналов. Даны примеры обработки акустических сигналов фильтрами Калмана первого и второго порядка.

Введение

Динамический анализ стохастических сигналов имеет важное значение при решении широкого круга научно-технических задач. Важным видом задач обработки является идентификация или определение параметров исследуемых процессов на основе анализа поступающей акустической информации. Для анализа сигналов, как правило, используются методы спектрального и стохастического анализа [1, 2]. Особенностью спектрального подхода является использование всехотсчетовданных, зарегистрированных ванализируемой выборке. Многие типичные исследуемые процессы имеют специфический спектральный состав и занимают характерные спектральные области, что позволяет легко выделять информативные составляющие сигналов. К недостаткам классического спектрального анализа относятся малая чувствительность к локальным свойствам сигналов, недостаточно высокое спектральное разрешение и сравнительно большие вычислительные затраты. Как правило, спектральный анализ проводится по выборке данных достаточно большой протяженности, и короткие локальные изменения не вносят значительного вклада в результирующий спектр сигнала. Вместе с тем, часто именно локальные изменения свойств сигналов, например, при ударных процессах, могут содержать полезную информацию. Большой объем обрабатываемых данных

исложные алгоритмы обработки требуют значительных вычислительных затрат при анализе спектров даже в случае использования быстрых алгоритмов типа быстрого преобразования Фурье(БПФ).

Методыстохастическогоанализа[3, 4] позволяютанализироватькакглобальные, таки локальные свойства сигналов в динамическом режиме и требуют меньших вычислительных затрат. Такие методы основываются на параметрических моделях, в структуре которых учитывается априорная информация об общих свойствах анализируемых сигналов. При использовании методов стохастической фильтрации ведется обработка только той информации, которая необходима в рамках решаемой задачи. Например, если известно, что следует анализировать данные только в определенной полосе частот, можно обойтись без спектрального преобразования и последующего анализа во всей спектральной области, используя фильтр Калмана для выделения в исходных данных необходимых спектральных областей.

Внастоящей работе рассмотрены параметрические модели сигналов и исследованы возможности динамической обработки стохастических сигналов фильтром Калмана первого

ивторого порядка для выделения информативных составляющих реальных акустических сигналов.

Метод фильтрации Калмана

Рассмотрим вначале дискретный линейный фильтр Калмана. Такой фильтр

Вуравнениях (1) и(2) s(k) - последовательностьрегистрируемыхдискретныхзначений сигнала, C(k) - матрица измерений, θ(k) - вектор параметров, n(k) - шум наблюдений, A(k) -

200

матрица перехода, w(k) - шум системы, k=1,...,K - номер отсчета дискретного сигнала. Обозначим ковариационные матрицы шумов n(k) и w(k) как Rn и Rw соответственно. Прогноз вектора параметров для шага k+1, согласно (2), можно определить в нулевом приближении как A(k)θ(k). Невязка между измеренным и прогнозированным значениями

где P(k+1) - коэффициент усиления фильтра Калмана.

Обозначим ковариационную матрицу погрешности предсказания вектора параметров θ(k+1) как Rpr(k+1), а ковариационную матрицу апостериорной оценки - как

R(k+1). Из (3) получим

R(k+1)=[I-P(k+1)C(k+1)]Rpr(k+1)[I-P(k+1)C(k+1)]T+P(k+1)RnPP T(k+1), (4)

где I - единичная матрица. Диагональные элементы матрицы R(k+1) представляют собой дисперсии компонентов вектора параметров, и коэффициент усиления P(k+1) следует выбирать так, чтобы эти дисперсии минимизировать.

Вследствие (2), можно записать выражение для ковариационной матрицы

Уравнение (6) определяет эволюцию ковариационной матрицы Rpr(k+1) погрешности предсказания параметров на каждом шаге. Оценка вектора параметров на следующем шаге (7) вычисляется с учетом коэффициента усиления, рассчитанного согласно (8). Ковариационная матрица апостериорной оценки параметров определяется выражением (9). Для применения алгоритма требуется знать начальные условия θ(0) и R(0), получаемые на этапе предварительной обработки сигнала.

Фильтр Калмана второго порядка

При необходимости выделения произвольной полосы частот узкополосных процессов использование фильтра Калмана первого порядка не эффективно. Для полосовой фильтрации стохастических сигналов целесообразно использовать фильтр Калмана второго порядка. Такой фильтр для скалярного дискретного случая определяется уравнениями:

θ1(k-1) = θ(k-1) - θ(k-2),

θ1(k) = θ1(k-1)-2aθ1(k-1)-b2θ(k-1)+ b2w(x), (10)

где a, b –коэффициенты, w(x) – белый шум.

Такой фильтр позволяет осуществлять фильтрацию узкополосного процесса, спектр мощности которого сосредоточен около некоторой центральной частоты в сравнительно узкой полосе частот. Спектральная плотность случайного процесса, определяемого уравнениями (10), имеет вид [3]:

201

при b2>>a2. Функция, определяемая уравнением (11), имеет максимумы на частотах ± b/2π, и ширина полосы пропускания фильтра определяется параметром a.

Фильтрация акустических сигналов

Фильтр Калмана первого порядка может быть исползован для выделения низкочастотных составляющих сигнала. Частотная характеристика такого фильтра

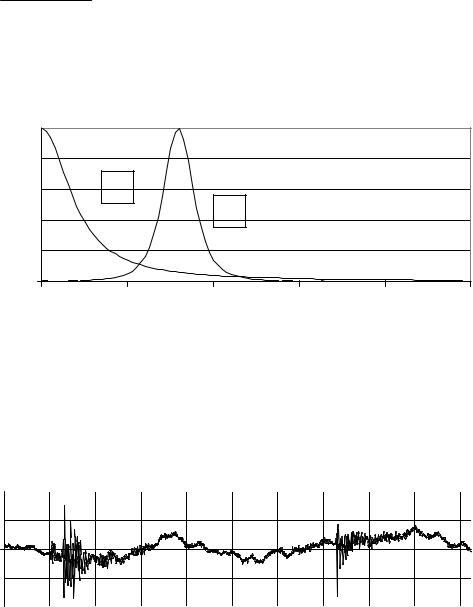
и имеет вид, показанный в левой части рис. 1. Выражение (12) определяет полуширину кривой спектральной плотности выходного сигнала при поступлении на вход фильтра гауссовского “белого” шума. Параметр a позволяет установить требуемую ширину полосы: чем больше величина этого параметра, тем более узкой является полоса пропускания фильтра первого порядка.

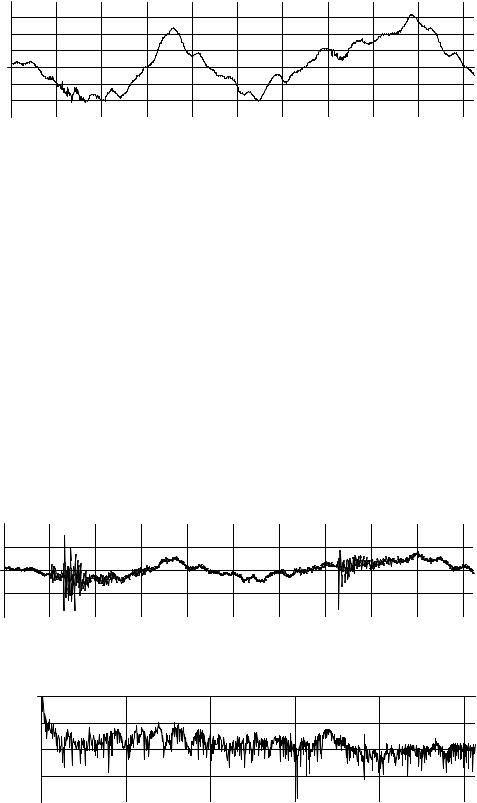
На рис. 2, а представлен пример реализации стохастического процесса в виде акустического сигнала, содержащего локальные участки с повышенными частотами на фоне медленно изменяющейся фоновой составляющей сигнала. Обработка сигналов такого вида при помощи традиционных методов спектрального анализа, как правило, не обеспечивает требуемого спектрального разрешения на локальных участках.

202

0,4

0,3

0,2

s(k ) 0,1 0

-0,1 -0,2 -0,3

k

Рис 2, б. Сигнал, полученный на выходе фильтра Калмана первого порядка

Результат выделения низкочастотных составляющих сигнала фильтром Калмана первого порядка представлен на рис. 2, б. Следует отметить, что фильтр Калмана обеспечивает динамическое формирование на его выходе сигнала, наиболее соответствующего заданной кривой спектральной плотности (12) в смысле минимума средней квадратической ошибки, из всех возможных реализаций случайного процесса.

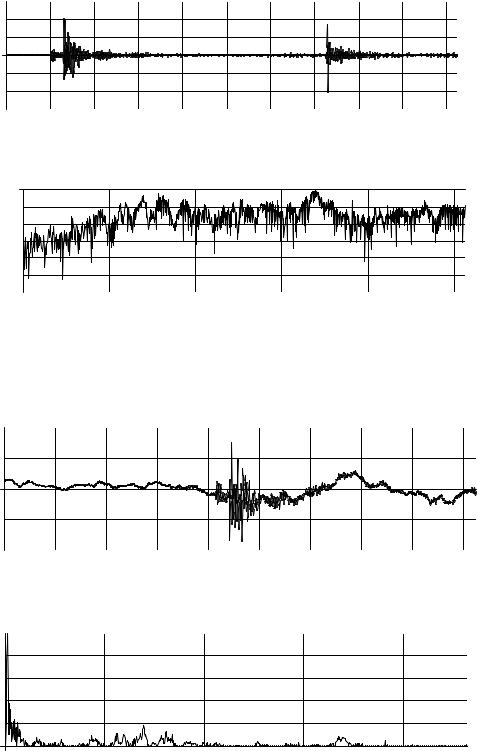
Очевидно, что с помощью фильтра первого порядка возможно также выделение высокочастотных составляющих сигнала путем вычитания из исходного сигнала предварительной отфильтрованных низкочастотных составляющих. Пример обработки этого вида применительно к акустическим сигналам приведен на рис. 3.

Кривые спектров рис. 3 наглядно иллюстрируют результат подавления спектральных составляющих в области нижних частот. Спектры S(u) вычислялись при помощи обычного алгоритма дискретного преобразования Фурье. Для большей наглядности кривые зависимостей модулей амплитудных спектров от значений дискретной частоты u представлены на рис. 3 в логарифмическом масштабе.

203

204