ВОССТАНОВЛЕНИЕ ЛИНИЙ ЭКСТРЕМУМОВ СЛОЖНЫХ КАРТИН ИНТЕРФЕРЕНЦИОННЫХ ПОЛОС

М.В. Волков

Анализ картин интерференционных полос имеет важное значение для задач неразрушающего контроля объектов. Во многих случаях интерференционные полосы искажены влиянием шумов и локальных дефектов, вследствие чего затруднена оценка их параметров. Представленный метод локальноадаптивной нелинейной фильтрации, основанный на модификации локальных гистограмм, обеспечивает помехоустойчивую обработку интерферограмм с восстановлением линий интерференционных экстремумов. Проведенные исследования показали высокую эффективность метода применительно к обработке сложных картин интерференционных полос.

Введение

Исследования свойств поверхностей различных объектов имеют важное значение для многих областей науки и техники. При этом предпочтительны неразрушающие оптические методы, эффективное применение которых требует использования помехоустойчивых алгоритмов обработки картин интерференционных полос. Обработка интерференционных сигналов и картин интерференционных полос необходима в муаровой [1-3] и голографической [4,5] интерферометрии. Во многих случаях интерференционные полосы искажены влиянием шумов, локальныхдефектовимогутиметьнизкий контраст, вследствие чего затруднена оценка фазы полос, содержащей информацию об исследуемом объекте или процессе. Известные методы обработки интерференционных полос на основе преобразования Фурье [6,7] или аппроксимации интерференционных полос нелинейными полиномами [8,9] часто не обеспечивают необходимой помехоустойчивости и требуют значительных вычислительных ресурсов при анализе реальных интерференционных картин. Таким образом, проблема разработки новых методов обработки и анализа картин полос являетсявесьмаактуальной.

Обычно требуется по картине интерференционных полос восстановить фазу полос или линии интерференционных экстремумов, однако это не всегда возможно без предварительной обработки картины полос. Основной задачей такой обработки является устранение шумов и локальных дефектов без снижения контраста полос. В работе исследован метод нелинейной локально-адаптивной обработки сигналов и изображений, основанный на модификации локальных гистограмм значений яркости. Эффективность метода обеспечивается разработанным алгоритмом настройки конфигурации и размеров локальнойобластифильтрациивзависимостиоттопологиикартиныполос. Приэтоманализ локальных характеристик полос может осуществляться по дисперсиям или приведенным производнымсигналавразличныхнаправлениях.

Представленный метод локально-адаптивной нелинейной фильтрации имеет ряд преимуществ перед стандартными методами обработки интерференционных полос. Метод позволяет обеспечить улучшение качества и анализ характеристик весьма сложных интерферограмм, обработка которых при традиционных подходах представляется проблематичной.

Адаптивная настройка параметров обработки позволяет решить задачу построения непрерывных линий экстремумов интерференционных полос. При этом качество восстановленных линий экстремумов превосходит известные алгоритмы отслеживания полос.

Обработка одномерных сигналов на основе модификации гистограмм

Рассмотрим вначале задачу обработки одномерного сигнала s(x) , который можно

рассматривать как сигнал в сечении двумерной интерференционной картины. Пусть реальный сигнал ξ(x) определяется моделью

162

где n(x) - аддитивная помеха с нулевым средним, и может принимать дискретные значения (уровни) ξi , i = 0,...,N . Выделим в области независимой переменной некоторый отрезок [a,b] и обозначим его среднюю точку xc . Будем считать, что оценка идеального сигнала s(xc ) может быть определена по значениям ξ(x) в точках дискретизации xk , k = 1,..., K , на выбранном отрезке. Для отрезка [a,b] построим эмпирическую гистограмму p(ξi ) , то есть оценку плотности вероятности, соответствующей закону распределения значений ξ(xk ) , xk [a,b] , по дискретным уровням ξi . Значение гистограммы для некоторого уровня ξi равно количеству точек

и т.д. Согласно (1), операция усреднения в (2) позволяет уменьшить влияние аддитивного шума.

Зададим на отрезке [a,b] некоторую функцию g(x) , обеспечивающую уменьшение вклада сигнала ξ(x) в гистограмму при удалении точки x от центра xc

отрезка фильтрации. Построим модифицированную гистограмму с учетом этой функции в форме

где xk : ξ(xk ) = ξi , xk [a,b] и α [1..3] .

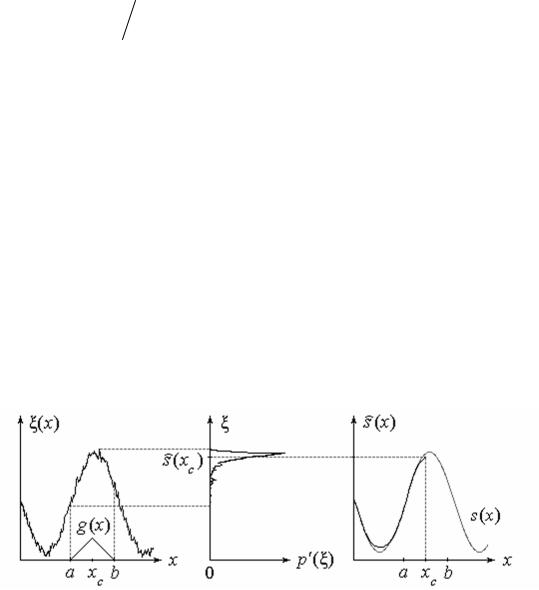
Таким образом, фильтрация одномерного сигнала методом модификации локальных гистограмм заключается в выполнении следующих операций (см. рис. 1):

•выбирается отрезок фильтрации [a, b] и на нем строится гистограмма (3);

•вычисляется среднее значение s)(xc ) по формуле (2), задающее значение s (x) в

средней точке отрезка;

• отрезок [a, b] сдвигается на шаг дискретизации x , после чего снова строится гистограмма и т.д.

Рис. 1. Восстановление сигнала методом модификации гистограмм с весовой

функцией

Особенностью метода (3) является сохранение амплитуды сигнала при итерационной обработке, когда оценка сигнала на n -ой итерации s)n (x) вычисляется

163

точек вблизи экстремумов, что приводит к незначительному изменению формы сигнала, и после нескольких шагов итерационной обработки появляются достаточно заполненные уровни. При этом предельно допустимые отклонения формы сигнала определяются видом весовой функции g(x) . В результате, начиная с некоторого шага

итерации, полностью прекращается снижение амплитуды сигнала, и дальнейшая обработка приводит лишь к уменьшению влияния помех. После подавления помех изменений сигнала не происходит. Это свойство сходимости итерационного алгоритма очень важно при обработке сигналов, искаженных влиянием пространственнонестационарных шумов и помех, которые характерны для реальных интерферограмм.

Важной особенностью метода является то, что для сигналов с близкой к нулю производной импульсные помехи в результате почти не оказывают влияния на выходной сигнал. Это объясняется тем, что “вес” каждого значения сигнала ξ(xk) ) при

модификации гистограммы, согласно (3), зависит от количества и удаленности значений сигнала ξ(xk ) , лежащих на том же уровне ξi . Значения на более заполненных

“стабильных” уровнях являются более устойчивыми, поэтому импульсные помехи оказывают на них очень слабое влияние.

Следует отметить, что увеличение локального периода сигнала приводит к значительному повышению эффективности фильтрации. Это свойство рассмотренного метода может быть использовано для повышения эффективности двумерной обработки картин полос, так как локальный период одномерного сигнала в сечении картины полос, проходящем через некоторую точку, зависит от направления.

Обработка картины полос

При переходе к обработке картин интерференционных полос необходимо обеспечить непрерывность по двум координатам. В простейшем случае значение оценки сигнала в некоторой точке определяется значениями сигнала во всех соседних точках некоторой двумерной области. При итерационной обработке возможно использование значений не во всех точках области, а лишь в некоторых сечениях, проходящих через точку, в которой определяется оценка сигнала. Такой подход позволяет значительно увеличить быстродействие метода, так как двумерная обработка может быть сведена к обработке одномерных сигналов.

Локальные периоды T (i, j,l) одномерных сигналов в различных сечениях l картины полос, проходящих через некоторую точку (i, j) , различны. В случае, когда направление сечения l совпадает с локальным направлением полос для точки (i, j) , период T (i, j,l) максимален, что позволяет с наибольшей эффективностью

использовать свойства предложенного метода.

При обработке картины интерференционных полос метод нелинейной фильтрации

(3) дает наилучшие результаты, если для каждой дискретной точки (i, j) направление

обработки l совпадает с локальным направлением полос. В этом случае помехи в одномерном сигнале устраняются наиболее эффективно, и не происходит снижения амплитуды сигнала. Однако такая обработка приводит к потере непрерывности по направлениям и искажению обработанной картины полос.

Для выполнения условия непрерывности обработки необходимо для каждой точки (i, j) картины полос вычислить оценки s (i, j,l) одномерных сигналов во всех сечениях

l , l =1, 2 , .. , L , проходящих через обрабатываемую точку, а затем с помощью некоторых “коэффициентов значимости” C(i, j,l) найти усредненное значение полученных оценок, а именно

164

направления l . Коэффициенты значимости имеют смысл “веса” оценки сигнала в сечении вдоль соответствующего направления. Эффективность нелинейного метода (3) зависит от локального периода сигнала T (i, j,l) , следовательно, и от направления

обработки l . Таким образом, настройка коэффициентов значимости позволяет повысить эффективность фильтрации. Чем меньше отклонение направления сечения l от локального направления полос, тем больше должен быть соответствующий коэффициент.

Коэффициенты значимости можно оценить по модулям приращений одномерных сигналов вдоль соответствующих направлений. По каждому направлению l для всей картины полос строятся модули приращений Δξ(i, j,l) = ξ(xk ) = ξ(xk +1 ) - ξ(xk −1 ) , где

xk−1 , xk и xk +1 – соседние точки сигнала в сечении вдоль указанного направления l . Полученные значения Δξ(i, j,l) отражают характер изменения производных

картины полос. Зависимость Δξ(i, j,l) от направления l позволяет определить

локальное направление полос. Однако, из-за влияния помех возможны значительные колебания параметра Δξ(i, j,l) для соседних точек картины полос, что ведет к

погрешности определения локального направления полос. Кроме этого, значение Δξ(i, j,l) как оценка производной сигнала полос зависит от фазы, что может приводить

к неправильной оценке направления полос. Так как для большинства реальных интерферограмм изменение направления полос в зависимости от изменения координат рассматриваемой точки достаточно мало, то простая двумерная фильтрация параметра Δξ(i, j,l) , например, в форме усреднения внутри некоторой маски A , в общем случае

не приводит к значительной потере точности оценки локального направления полос. Размер маски усреднения A необходимо выбирать в зависимости от топологии полос. Увеличение размера маски уменьшает влияние помех, но при этом происходит снижение чувствительности параметра к достаточно быстрым изменениям направления полос. В наиболее простом случае размер маски можно выбрать равным среднему значению шага полос.

В случае, если картина полос не содержит резких изломов, т.е. изменение направления полос мало, размер маски усреднения A может быть в десятки раз больше шага полос. В этом случае за счет использования данных от соседних полос удается сохранить оценку правильного направления при значительных локальных дефектах, в том числе, при разрыве нескольких полос.

Полученные результаты усреднения значений Δξ(i, j,l ) , где l – номер направления, перпендикулярного l , по некоторой маске A задают значение C(i, j,l) .

Будем для простоты полагать, что помехи оказывают одинаковое влияние на коэффициенты C(i, j,l) , т.е. что влияние помех изотропное. При совпадении

направления полос с направлением обработки l в некоторой точке (i, j) значение C(i, j,l) максимально. С другой стороны, если направление сечения перпендикулярно к интерференционным полосам, значение C(i, j,l) минимально.

Задача определения размеров отрезков фильтрации одномерных сигналов в различных направлениях для каждой точки картины полос может быть решена с использованием коэффициентов значимости C(i, j,l) .

Размеры отрезков фильтрации, очевидно, должны зависеть от шага интерференционных полос. Для эффективной фильтрации необходимо более широкие интерференционные полосы обрабатывать с большим отрезком фильтрации, более

165

узкие – с меньшим. Такая обработка позволяет сохранить контрастность полос малой ширины, то есть не приводит к потере информации о картине полос.

Для получения оценок локального шага полос во всех точках интерферограммы, необходимо вначале оценить значение шага полос хотя бы в одной точке. Простейшим случаем такой оценки является задание значения минимального шага полос как исходного глобального параметра интерферограммы. Усредненные по направлениям коэффициенты значимости

содержат информацию об изменении шага полос. По усредненным коэффициентам значимости можно судить об изменении шага полос в предположении о неизменности амплитуды и уровня помех для всех точек картины полос. Таким образом, с помощью данных коэффициентов можно получить оценки шага полос в каждой точке интерферограммы.

Относительные размеры отрезков фильтрации в различных сечениях для некоторой точки могут быть определены с помощью коэффициентов значимости C(i, j,l) . При обработке сигнала в направлении, соответствующему направлению

полос, размер отрезка фильтрации может быть достаточно большим, это позволяет лучше подавлять помехи и не приводит к снижению амплитуды полос. В то же время, при обработке сигнала в сечении, перпендикулярном направлению полос, следует выбирать меньший отрезок фильтрации.

Таким образом, для определения размеров отрезков фильтрации по заданному минимальному шагу полос и соответствующему отрезку фильтрации для каждой точки картины полос через коэффициенты значимости находится локальный шаг полос, и по нему определяется средний размер отрезка фильтрации K (i, j) . После этого размеры

отрезков фильтрации в точке (i, j) вычисляются с помощью коэффициентов значимости по формуле

K(i, j,l) = K(i, j)C(i, j,l)C(i, j) ,

где C(i, j,l) определяются из выражения (5).

Для выполнения одного шага итерации при обработке картины интерференционных полос, необходимо для каждой точки картины полос для всех направлений l определить размеры отрезков фильтрации K (i, j,l) , определить

коэффициенты значимости, найти оценки s (i, j,l) одномерных сигналов и усреднить их по формуле (4).

Рис. 2. Пример обработки реальной двумерной интерференционной картины

итерационным методом нелинейной фильтрации на основе модификации локальных гистограмм

В качестве примера на рис. 2, а показана искаженная картина интерференционных полос форматом 200×150 точек, квантованная по 256-ти уровням. Для одной из точек

166