Матричные игры

Рассмотрим игру, в которой участвую два игрока, причем каждый из них имеет конечное число стратегий.

Обозначим для удобства одного из игроков через А, а другого – через В.

Предположим что игрок А имеет m стратегий: ,,…,, а игрокB – n стратегий: ,,,…,.

Пусть игрок А выбрал стратегию , а игрокВ – стратегию .

Будем считать, что выбор игроками стратегий иоднозначно определяет исход игры – выигрышигрокаА и выигрыш игрока В, причем эти выигрыши связаны равенством .

Последнее обстоятельство показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с отрицательным знаком, т. е. проигрышу. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будут, например, выигрыши игрока А.

Если нам известны значения выигрыша при каждой паре стратегий (в каждой ситуации)и,i = 1, 2, …, m, k = 1, 2, …, n, то их удобно представить записывать

или в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В.

				…
				…
				…
…	…	…	…	…	…
				…

или в виде матрицы

Полученная матрица имеет размер m  n и называется матрицей игры или платежной матрицей (отсюда и название игры – матричная).

Рассматриваемую игру часто называют игрой m  n или m  n-игрой.

Замечание. Матричные игры относятся к разряду так называемых антагонистических игр, т. е. игр, в которых интересы игроков прямо противоположны.

Равновесная ситуация

Рассмотрим следующий пример.

Два игрока А и В, не глядя друг на друга, кладут на стол по картонному кружку красного (К), зеленного (З) или синего цвета (С), сравнивают цвета кружков и расплачиваются друг с другом так, как показано в матрице игры:

	-2	2	-1
	2	1	1
	3	-3	1

Считая, что эта игра повторяется многократно, попробуем определить оптимальные стратегии каждого из игроков.

Начнем с последовательного анализа стратегии игрока А, не забывая при этом, что его противник, игрок В, может ответить той из своих стратегий, при которой выигрыш игрока А будет минимальным.

Так, на стратегию игрокаА его противник может ответить стратегией (минимальный выигрыш равен – 2, что на самом деле означает проигрыш игрокаА, равный 2), на стратегию

Смешанные стратегии

Пример. Швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависит от состояния погоды. По данным прошлых наблюдений предприятие в течение апреля – мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде – 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции составляют для костюмов 27 ден. ед., для платьев 8 ден. ед., а цена реализации равна соответственно 48 ден. ед. и 16 ден. ед.

Задача заключается в максимизации средней величины прибыли от реализации выпущенной продукции с учетом неопределенности погоды в рассматриваемые месяцы. Таким образом, служба маркетинга предприятия должна в этих условиях определить оптимальную стратегию предприятия, обеспечивающую при любой погоде средний доход. Решим эту задачу методами теории игр, игра в этом случае будет относиться к типу игр с природой.

Предприятие в этих условия располагает двумя чистыми стратегиями: стратегия - в расчете на теплую погоду и стратегия- в расчете на прохладную погоду. Природу будем рассматривать как второго игрока также с двумя стратегиями: прохладная погода – стратегияи теплая погода – стратегия. Если предприятие выберет стратегиюв расчете на теплую погоду, то в случае прохладной погоды (стратегия природы) доход составит

руб.,

а в случае теплой погоды (стратегия природы ) доход будет равен

руб.

Если предприятие выберет стратегию в расчете на прохладную погоду, то реализация продукции в условиях прохладной погоды (стратегия природы) даст доход

руб.,

а в условиях теплой погоды (стратегия природы )

руб.

Следовательно, матрица данной игры (платежная матрица) имеет вид:

.

Первая и вторая строки этой матрицы стратегиям ипредприятия, а первый второй столбцы – стратегиямиприроды.

По платежной матрице видно, что первый игрок (предприятие) никогда не получит доход меньшие 6800 руб. Но если погодные условия совпадают с выбранной стратегией, то выигрыш (доход) составит 26000 или 28000 руб. Отсюда можно сделать вывод, что в условиях неопределенности погоды наибольший гарантированный доход предприятие обеспечит, если будет попеременно применять то стратегию , то стратегию. Такая стратегия называется смешанной. Оптимизация смешанной стратегии позволит первому игроку всегда получать среднее значение выигрыша независимо от стратегии второго игрока.

Пусть означает частоту применения первым игроком стратегии, тогда частота применения им стратегииравна. В случае оптимальной смешанной стратегии первый игрок (предприятие) получит при любой стратегии второго игрока одинаковый средний доход:

.

Отсюда можно найти, что ;.

Следовательно, первый игрок, применяя чистые стратегии ив соотношении 8:9, будет иметь оптимальную смешанную стратегию, обеспечивающую ему в любом случае средний доход в суммеруб.; эта величина и будет в данном случае ценой игры.

Легко рассчитать, какое количество костюмов и платьев должно выпускать предприятие при оптимальной смешанной стратегии:

(600 костюмов + 1975 платьев)  8/17 +(1000 костюмов + 625 платьев)  9/17 =

= 812 костюмов + 1260 платьев.

Следовательно, оптимальная стратегия предприятия заключается в выпуске 812 костюмов и 1260 платьев, что обеспечит ему при любой погоде средний доход в сумме 16965 руб.

В случае когда нижняя цена игры  и верхняя цена игры  не совпадают, игрокА может обеспечить себе выигрыш, не меньший , а игрок В имеет возможность не дать ему больше, чем .

Возникает вопрос: а как разделить между игроками разность ?

Предыдущие построения на этот вопрос ответа не дают – тесны рамки возможных действий игроков.

Поэтому довольно ясно, что механизм, обеспечивающий получение каждым из игроков как можно большей доли этой разности, следует искать в определенном расширении стратегических возможностей, имеющихся у игроков изначально.

Оказывается, что компромиссного распределения разности между игроками и уверенного получения каждым игроком своей доли при многократном повторении игры можно достичь путем случайного применения ими своих первоначальных, чистых стратегий.

ИГРА 2n

Рассмотрим игру с платежной матрицей

				…

Игрок А обладает двумя чистыми стратегиями и, а игрокВ – n чистыми стратегиями ,,,…,.

ЭЛЕМЕНТЫ ТЕОРИИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ

Задачи организации массового обслуживания возникают во многих областях практической деятельности. В частности, предприятия бытового обслуживания и общественного питания, торговля и заготовительные предприятия, поликлиники и телефонные станции, билетные кассы могут служить типичными примерами систем массового обслуживания, которые удовлетворяют потребности населения в услугах определенного вида. Очевидно, качество обслуживания зависит от пропускной способности СМО. В свою очередь пропускная способность СМО зависит от количества обслуживающих единиц и их производительности. С другой стороны, с ростом числа и производительности обслуживающих единиц увеличиваются затраты связанные с их функционированием. При этом возникает необходимость экономической обоснованности этих затрат.

Работа любой системы массового обслуживания состоит в выполнении поступающего на нее потока требований и заявок. Заявки поступают одна за другой в некоторые, вообще говоря, случайные, моменты времени. Обслуживание поступившей заявки продолжается какое-то время, после чего канал освобождается и снова готов для приема следующей заявки. Каждая система массового обслуживания, в зависимости от числа каналов и их производительности, обладает какой-то пропускной способностью, позволяющей ей более или менее успешно справляться с потоком заявок. Предмет теории массового обслуживания – установление зависимости между характером потока заявок, производительностью отдельного канала, числом каналов и успешностью (эффективностью) обслуживания. В качестве характеристик эффективности обслуживания - в зависимости от условий задачи и целей исследования – могут применяться различные величины и функции, например: средний процент заявок, получающих отказ и покидающих систему не обслуженными; среднее время «простоя» отдельных каналов и системы в целом; среднее время ожидания в очереди; вероятность того, что поступившая заявка немедленно будет принята к обслуживанию; закон распределения длины очереди и т. д. Каждая из этих характеристик описывает, с той или другой стороны, степень приспособленности системы к выполнению потока заявок, иными словами – ее пропускную способность.

Однако пропускная способность в общем зависит не только от параметров СМО, но и от характера потока заявок. Если бы заявки поступали регулярно, через точно определенные промежутки времени, и обслуживание каждой заявки имело строго определенную длительность, расчет пропускной способности системы не представлял бы ни какой трудности. На практике обычно моменты поступления заявок случайны, по большей части случайна и длительность обслуживания заявки. В связи с этим процесс работы системы протекает нерегулярно: в потоке заявок образуются местные сгущения и разряжения. Сгущения могут привести либо к отказам в обслуживании, либо к образованию очередей. Разряжения могут привести к непроизводительным простоям отдельных каналов или системы в целом. На эти случайности, связанные с неоднородностью потока заявок, накладываются еще и случайности, связанные с задержками обслуживания отдельных заявок. Таким образом, процесс функционирования СМО представляет собой случайный процесс. Чтобы дать рекомендации по рациональной организации системы, выяснить ее пропускную способность и предъявить к ней требования, необходимо изучить случайный процесс, протекающий в системе, и описать его математически. Этим и занимается система массового обслуживания.

Поток событий. Простейший поток и его свойства.

Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции, поток включений приборов в бытовой электросети; поток заказных писем, поступающих в почтовое отделение, поток заявок на обслуживание клиентов, поступающих в склад и т. д. События, образующие поток, в общем виде могут различными, но здесь мы будем рассматривать лишь поток однородных событий, различающихся только моментами появления. Такой поток можно изобразить как последовательность точек ,, …,, … на числовой оси, соответствующих моментам появления событий.

Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Такой поток сравнительно редко встречается в реальных системах, но представляет интерес как предельный случай. Типичным для СМО является случайный поток заявок.

Рассмотрим потоки событий, обладающие некоторыми особенно простыми свойствами. Для этого введем ряд определений.

1. Поток событий называется стационарным, если вероятность попадания того или иного числа событий на определенный отрезок времени зависит только от длины этого отрезка и не зависит от того, где именно на числовой оси, характеризующей время, расположен этот участок.

2. Поток событий называется потоком без последствий, если для любых неперекрывающихся отрезков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

3. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Если поток событий обладает всеми тремя свойствами, перечисленными выше, то он называется простейшим (или стационарным пуассоновским) потоком. Название «пуассоновский» связано с тем, что при соблюдении условий 1 – 3 число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона.

Рассмотрим подробнее условия 1 – 3, посмотрим, чему они соответствуют для потока заявок и за счет чего они могут нарушаться.

1. Условию стационарности удовлетворяет поток заявок, вероятностные характеристики которого не зависят от времени. В частотности, для стационарного потока характерна постоянная плотность (среднее число заявок в единицу времени). На практике часто встречаются потоки заявок, которые (по крайней мере, на ограниченном отрезке времени) могут рассматриваться как стационарные. Например, поток вызовов на городской телефонной станции на участке времени от 12 до 13 часов может считаться стационарным. Тот же поток в течение целых суток уже не может считаться стационарным (ночью плотность вызовов значительно меньше, чем днем). Заметим, что так обстоит дело и со всеми физическими процессами, которые мы называем «стационарными»: в действительности все они стационарны лишь на ограниченном участке времени, а распространение этого участка до бесконечности – лишь удобный прием, применяемый в целях упрощения анализа. Во многих задачах теории массового обслуживания представляет интерес проанализировать работу системы при постоянных условиях; тогда задача решается для стационарного потока заявок.

2. Условие отсутствия последствия – наиболее существенное для простейшего потока – означает, что заявки поступают в систему независимо друг от друга. Например, поток пассажиров в метро, можно считать потоком без последствий потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не другой момент, как правило, не завязаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последствий может быть легко нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последствия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой.

Вообще нужно заметить, что выходной поток (или поток обслуженных заявок), покидающих систему массового обслуживания, обычно имеет последствие, даже если входной поток его не имеет. Последствие, присущее выходному потоку, необходимо учитывать, если этот поток является входным для какой-либо другой системы массового обслуживания (так называемое «многофазовое обслуживание», когда одна и та же заявка последовательно переходит из одной системы в другую).

3. Условие ординарности означает, что заявки приходят по одиночке, а не парами.

Простейший поток играет среди потоков событий вообще особую роль, до некоторой степени аналогичную роли нормального закона среди других законов распределения. Мы знаем, что при суммировании большого числа независимых случайных величин, подчиненных практически любым законом распределения, получается величина, приближенно распределенная по нормальному закону. Аналогично можно доказать, что при суммировании (взаимном наложении) большого числа ординарных, стационарных потоков с практически любым последствием получается поток, сколь угодно близкий к простейшему. Условия, которые должны для этого соблюдаться, аналогичны условиям центральной предельной теоремы, а именно – складываемые потоки должны оказывать на сумму приблизительно равномерно малое влияние.

На практике оказывается обычно достаточно сложить 4 – 5 потоков, чтобы получит поток, с которым можно оперировать как с простейшим.

Простейший поток играет в теории массового обслуживания особую роль. Во-первых, простейшие и близкие к простейшим потоки заявок часто встречаются на практике (причины этого изложены выше). Во-вторых, даже при потоке заявок, отличающемся от простейшего, часто можно получить удовлетворительные по точности результаты, заменив поток любой структуры простейшим с той же плотностью.

Рассмотрим на простейший поток событий как неограниченную последовательность случайных точек.

Выделим произвольный участок времени длинной . Вероятность того, что за время  произойдет ровно m событий, равна

где  - интенсивность потока заявок, т. е. среднее число заявок, приходящихся на единицу времени:

,

где  - среднее значение интервала между двумя соседними заявками.

В частности, вероятность того, что отрезок окажется пустым (не произойдет ни одного события), будет равна

Важной характеристикой потока является закон распределения длины промежутка между соседними событиями. Рассмотрим случайную величину T – промежуток времени между произвольными двумя соседними событиями в простейшем потоке и найдем ее функцию распределения

.

Перейдем к вероятности противоположного события

.

Это есть вероятность того, что на отрезке времени длиной t, начинающемся в момент появления одного из событий потока, не появится ни одного из последующих событий. Так как простейший поток не обладает последствием, то наличие в начале отрезка (в точке) какого-то события никак не влияет на вероятность появления других событий в дальнейшем. Поэтому вероятностьможно вычислить по формуле

,

откуда

.

Дифференцируя, найдем плотность распределения

. (*)

Закон распределения с плотностью (*) называется показательным законом, а величина - его параметром.

Математическое ожидание, дисперсия и среднеквадратическое отклонение для случайной величины распределенной по показательному закону соответственно равны

, ,.

Показательный закон распределения обладает одним замечательным свойством, а именно: если промежуток времени, распределенный по показательному закону, уже длился некоторое время, то это никак не влияет на закон распределения оставшейся части промежутка.

Время обслуживания.

Кроме характеристик входного потока заявок, режим работы системы зависит еще от характеристик производительности самой системы: числа каналов n и быстродействия каждого канала. Одной из важнейших величин, связанных с системой, является время обслуживания одной заявки . Эта величина может быть как неслучайной, так и случайной. Очевидно, более общим является случайное время обслуживания.

Рассмотрим случайную величину и обозначимее функцию распределения:

.

а - плотность распределения:

.

Для практики особый интерес представляет случай, когда величина имеет показательный закон распределения

где параметр  - интенсивность потока обслуживания, величина, обратная среднему времени обслуживания одной заявки:

,

где - среднее время обслуживания.

Марковский случайный процесс

Допущения о пуассоновском характере потока заявок и о показательном распределении времени обслуживания позволяют применить к теории массового обслуживания аппарат так называемых марковских случайных процессов.

Процесс, протекающий в физической системе, называется марковским, (или процессом без последствия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент времени и не зависит от того, каким образом система пришла в это состояние.

Система массового обслуживания с отказами. Установившийся режим обслуживания. Формулы Эрланга.

В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует.

Пусть имеется n-канальная система массового обслуживания с отказами. Рассмотрим ее как физическую систему с конечным множеством состояний:

- свободны все каналы,

- занят ровно один канал,

…..

- занято ровно k каналов,

…..

- заняты все n каналов.

Схема возможных переходов дана на рисунке.

На вход системы подается простейший поток заявок с интенсивностью , время обслуживания заявки показательное с параметром . Очевидно, что в начале, сразу после включения системы в работу, протекающий в ней процесс не будет стационарным: в системе массового обслуживания (как и в любой динамической системе) возникает так называемый «переходный», нестационарный процесс. Однако, спустя некоторое время, этот переходный процесс затухнет, и система перейдет на стационарный, так называемый «установившийся» режим, вероятностные характеристики которого уже не будут зависеть от времени.

Формулы для установившегося режима.

1. Вероятность простоя каналов, когда нет заявок:

.

где –интенсивность нагрузки.

2. Вероятность того, что k-каналов занято обслуживанием заявок:

.

3. Вероятность отказа в обслуживание, когда все каналы заняты:

.

4. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:

.

5. Среднее число занятых обслуживанием каналов:

.

6. Абсолютная пропускная способность

Система массового обслуживания с ожиданием.

Система массового обслуживания называется системой с ожиданием, если заявка, заставшая все каналы занятыми, становится в очередь и ждет, пока не освободится какой-нибудь канал.

Пусть имеется n-канальная система массового обслуживания с ожиданием. Возможные состояния системы будут:

- свободны все каналы,

- занят ровно один канал,

…..

- занято ровно k каналов,

…..

- заняты все n каналов,

- заняты все n каналов, одна заявка стоит в очереди,

…..

- заняты все n каналов, s заявок стоит в очереди,

…..

Число заявок, стоящих в очереди, может быть сколь угодно большим. В такой системе не всегда имеется установившийся режим. Такой режим существует только при , т. е. когда интенсивность нагрузки не выходит за пределы возможностейn-канальной системы. Если же , число заявок, стоящих в очереди будет с течением времени неограниченно возрастать.

Основной характеристикой качества обслуживания является время ожидания обслуживания.

Для таких систем характерно отсутствие отказа в обслуживании, т. е. ,.

Для систем с ожиданием существует дисциплина очереди:

1. обслуживание в порядке очереди по принципу «первым пришел – первым обслужен»;

2. случайное неорганизованное обслуживание;

3. обслуживание с приоритетами.

Формулы для установившегося режима.

1. Вероятность простоя каналов, когда нет заявок:

.

2. Вероятность того, что k-каналов занято обслуживанием заявок:

.

3. Вероятность того, что все каналы заняты обслуживанием:

4. Среднее число занятых каналов:

5. Среднее число свободных каналов:

6. Среднее число заявок находящихся в очереди:

7. Среднее число заявок находящихся в системе:

8. Среднее время обслуживания заявки:

9. Среднее время ожидания заявки в очереди на обслуживание:

10. Среднее время пребывания заявки в СМО:

СМО с ожиданием и с ограничением на длину очереди

В системе с ожиданием и ограничением на длину очереди заявка, поступившая в момент, когда все каналы и все места в очереди заняты, получает отказ в обслуживание.

Пусть имеется n-канальная система массового обслуживания с ожиданием, в которой количество заявок в очереди ограничено числом m. Возможные состояния системы будут:

- свободны все каналы,

- занят ровно один канал,

…..

- занято ровно k каналов,

…..

- заняты все n каналов,

- заняты все n каналов, одна заявка стоит в очереди,

…..

- заняты все n каналов, m заявок стоит в очереди.

Формулы для установившегося режима.

1. Вероятность простоя каналов, когда нет заявок:

.

2. Вероятность того, что k-каналов занято обслуживанием заявок:

.

3. Вероятность того, что в системе пребывает n+s заявок:

.

4. Вероятность отказа в обслуживании:

5. Вероятность обслуживания:

6. Абсолютная пропускная способность:

7. Среднее число занятых каналов:

8. Среднее число свободных каналов:

9. Среднее число заявок находящихся в очереди:

10. Среднее число заявок находящихся в системе:

11. Среднее время ожидания обслуживания:

12. Среднее время ожидания заявки в очереди на обслуживание:

13. Среднее время пребывания заявки в СМО:

Определение эффективности трудовых и производственных ресурсов в СМО

Рассмотрим задачу с использованием СМО с отказами.

Пример 1. В ОТК цеха работают три контролера. Если деталь поступает в ОТК, когда все контролеры заняты обслуживанием ранее поступивших деталей, то она проходит отдел непроверенной. Среднее число деталей, поступающих в ОТК в течение часа, равно 24, среднее время, которое затрачивает контролер на обслуживание одной детали, равно 5 мин. Определить вероятность того, что деталь пройдет ОТК необслуженной, насколько загружены контролеры и сколько их необходимо поставить, чтобы (* - заданное значение).

Решение: По условию задачи , мин, тогда,.

1. Вероятность простоя каналов, когда нет заявок:

.

2. Вероятность отказа в обслуживание, когда все каналы заняты:

.

3. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:

.

4. Среднее число занятых обслуживанием каналов:

.

5. Абсолютная пропускная способность

При .

Произведем аналогичные расчеты при :

1. Вероятность простоя каналов, когда нет заявок:

.

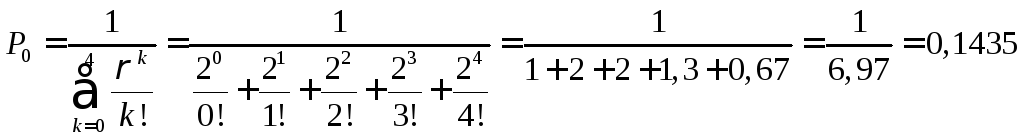2. Вероятность отказа в обслуживание, когда все каналы заняты:

.

3. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:

.

При .

Произведем аналогичные расчеты при :

4. Вероятность простоя каналов, когда нет заявок:

.

5. Вероятность отказа в обслуживание, когда все каналы заняты:

.

6. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:

.

При .

Ответ. Вероятность того, что при деталь пройдет ОТК необслуженной, составляет 21%, и контролеры будут загружены обслуживанием на 53%.

Чтобы обеспечить вероятность обслуживания более 95%, необходимо не менее пяти контролеров.

Рассмотрим задачу с использованием СМО с неограниченным ожиданием.

Пример 2. Сберкасса имеет трех контролеров-кассиров для обслуживания вкладчиков. Каждый день в сберкассу обращается за обслуживанием в среднем около 240 человек. Рабочий день длится 8 часов. Средняя продолжительность обслуживания контролером-кассиром одного вкладчика 3 мин.

Определить характеристики сберкассы как объекта СМО.

Решение. По условию задачи ,, , тогда,. Так как, следовательно, в СМО существует установившийся режим работы.

1. Вероятность простоя каналов, когда нет заявок:

.

2. Вероятность того, что все каналы заняты обслуживанием:

.

3. Среднее число занятых каналов:

.

4. Среднее число свободных каналов:

.

5. Среднее число заявок находящихся в очереди:

.

6. Среднее число заявок находящихся в системе:

7. Среднее время ожидания заявки в очереди на обслуживание:

мин.

8. Среднее время пребывания заявки в СМО:

мин.

Ответ. Вероятность простоя контролеров-кассиров равна 21% рабочего времени, вероятность посетителю оказаться в очереди составляет 11,8%, среднее число посетителей в очереди 0,236 чел., среднее время ожидания посетителями обслуживания 0,472 мин.

Рассмотрим задачу с применением СМО с ожиданием и с ограничением на длину очереди.

Пример 3. На автозаправочной станции установлены 3 бензоколонки. Около станции находится площадка на 3 автомобиля для ожидания заправки, в случае если бензоколонки заняты. В течение часа на автозаправочную станцию пребывает в среднем 75 автомобилей. Среднее время обслуживания одного автомобиля 2 мин.

Определить все характеристики автозаправочной станции как объекта СМО. Какова должна быть вместимость площадки для ожидания обслуживания, чтобы заданная вероятность обслуживания .

Решение. По условию задачи ,,, , тогда,.

1. Вероятность простоя каналов, когда нет заявок:

2. Вероятность отказа в обслуживании:

3. Вероятность обслуживания:

4. Абсолютная пропускная способность:

5. Среднее число занятых каналов:

6. Среднее число свободных каналов:

7. Среднее число заявок находящихся в очереди:

8. Среднее число заявок находящихся в системе:

9. Среднее время ожидания обслуживания:

10. Среднее время ожидания заявки в очереди на обслуживание:

11. Среднее время пребывания заявки в СМО:

При .

Произведем аналогичные расчеты при :

1. Вероятность простоя каналов, когда нет заявок:

2. Вероятность отказа в обслуживании:

3. Вероятность обслуживания:

При .

Произведем аналогичные расчеты при :

1. Вероятность простоя каналов, когда нет заявок:

2. Вероятность отказа в обслуживании:

3. Вероятность обслуживания:

При .

Ответ. Вероятность того, что при автомобиль будет обслужен автозаправочной станцией составляет 86%. Чтобы обеспечить вероятность обслуживания более 90%, необходимо не менее пяти мест ожидания заправки.