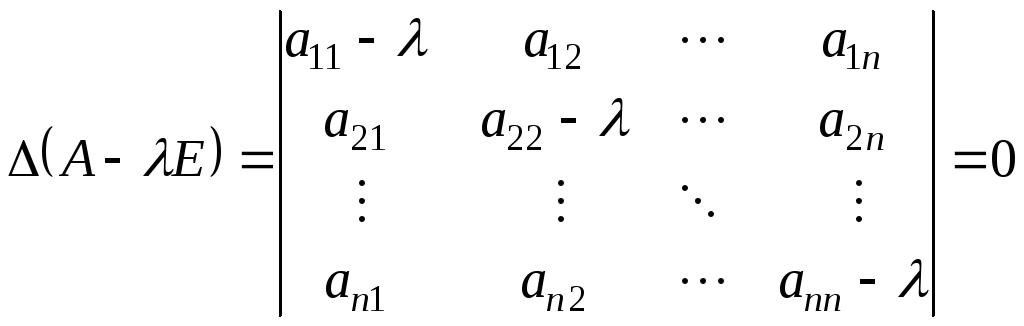1.3. Ранг матрицы

Рассмотрим матрицу размераВычеркиванием каких–либо строк или столбцов можно вычленить квадратные подматрицы-го порядка, гдеОпределители таких подматриц называются минорами-го порядка матрицы.

Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.

Обозначают ранг матрицы обычно или.

Свойства ранга матрицы

1. Ранг матрицы 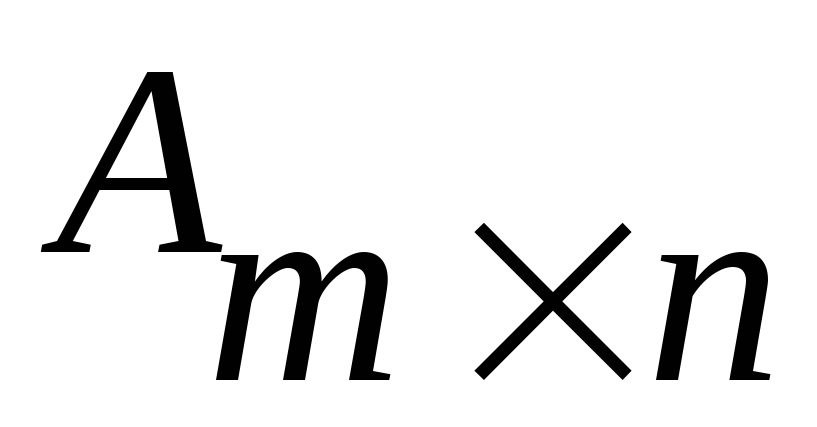не превосходит меньшего из ее размеров, т.е.

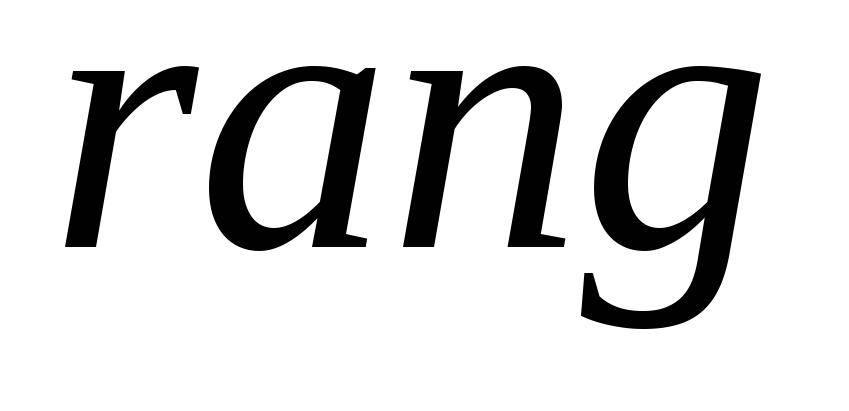
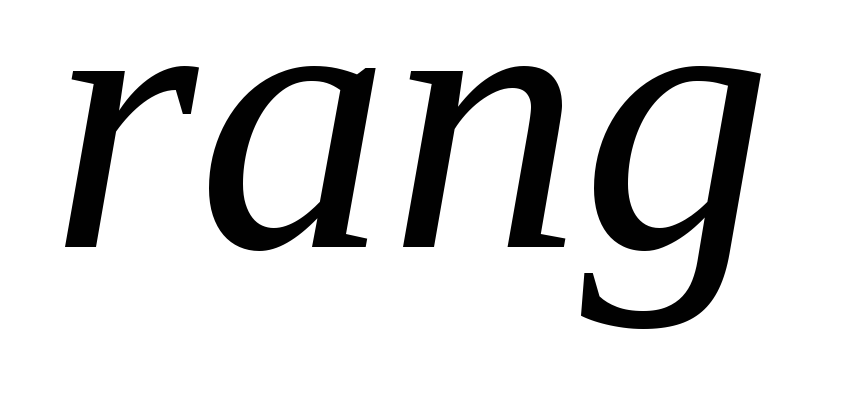
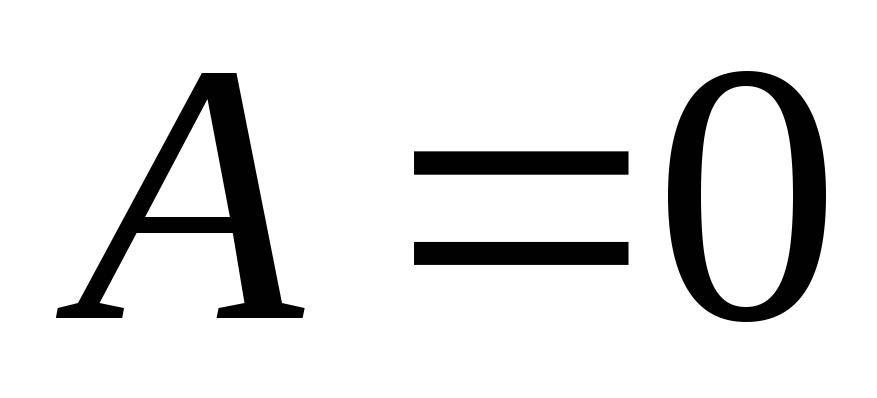2. тогда и только тогда, когда – нулевая матрица.

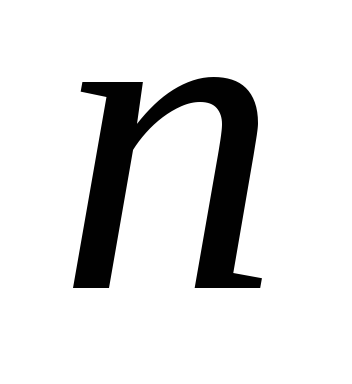3. Если – квадратная матрица-го порядка, то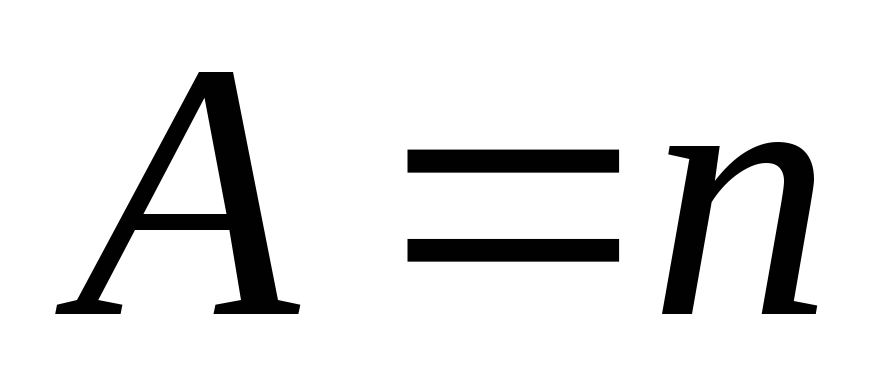тогда и только тогда, когда матрицаневырожденная.

Нахождение ранга матрицы, используя непосредственно определение, довольно громоздко и трудоемко.

Теорема 4. Ранг матрицы не изменяется при ее элементарных преобразованиях.

С помощью элементарных преобразований можно привести матрицу к верхнетреугольному виду:

,

где ,;.Ранг верхнетреугольной матрицы равен .

Пример 12. Найти ранг матрицы .

Решение. Используя технику элементарных преобразований (как в методе Гаусса), получим верхнетреугольную матрицу:

Таким образом, .n

Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк (столбцов).

Строка (столбец) называются линейно зависимыми, если хотя бы одна из строк (столбцов) линейно выражается через остальные. В противном случае, строки (столбцы) называются линейно независимыми (подробнее читайте в п. 1.6.1).

Теорема 5. Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).

1.4. Собственные векторы и собственные значения матрицы

Вектор называется собственным вектором матрицы, если найдется такое число, что

(1.6)

Число называетсясобственным значением матрицы , соответствующим вектору.

Равенство (1.6) можно записать в развернутом виде:

.

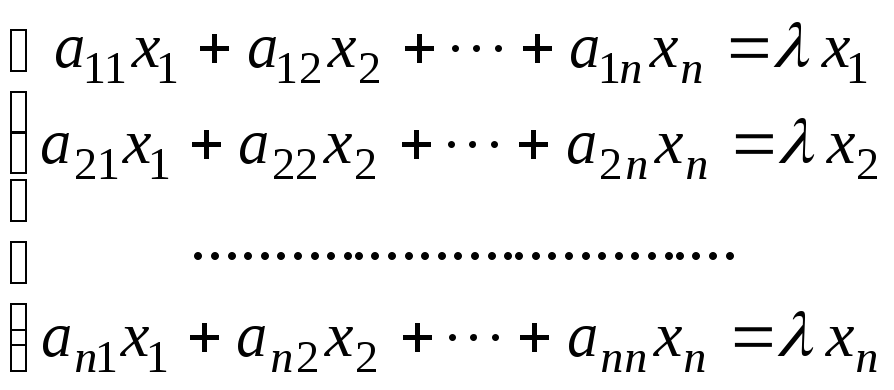Откуда получим

или в матричном виде

.

Полученная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы обращался в нуль:

(1.7)

Определитель является многочленом-ой степени. Он называетсяхарактеристическим многочленом матрицы , а уравнение (1.7)–характеристическим уравнением матрицы .

Теорема 6. Корни характеристического уравнения матрицы (если они существуют) и только они являются собственными значениями этой матрицы.

Пример 13. Найти собственные значения и собственные векторы матрицы:

.

Решение. Составим характеристическое уравнение

или ,

откуда собственные значения матрицы :,.

Находим собственный вектор , соответствующий собственному значению. Для этого решаем матричное уравнение:

или ,

откуда , т.е.. Положив, мы получим, что векторпри любомявляется собственным вектором матрицыс собственным значением. Аналогично, получим, что векторпри любомявляется собственным вектором матрицыс собственным значением.n

Пример 14. Найти собственные значения и собственные векторы матрицы:

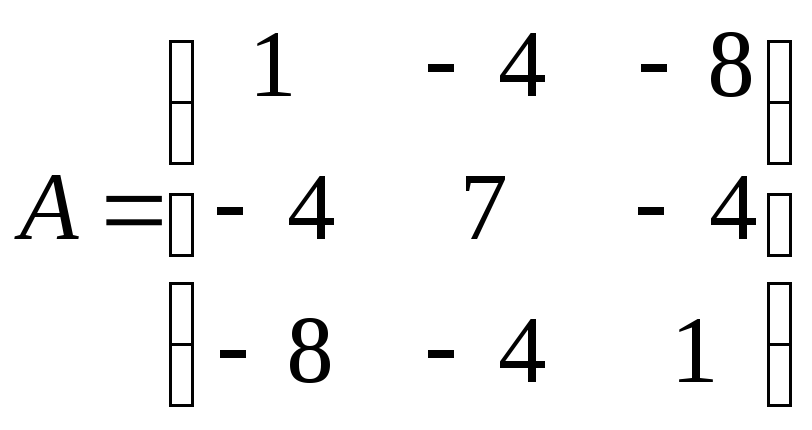
Решение. После преобразований (проделайте это самостоятельно) характеристическое уравнение примет вид:

.

Имеем далее

,

откуда ,.

Найдем собственный вектор , соответствующий собственному значению:

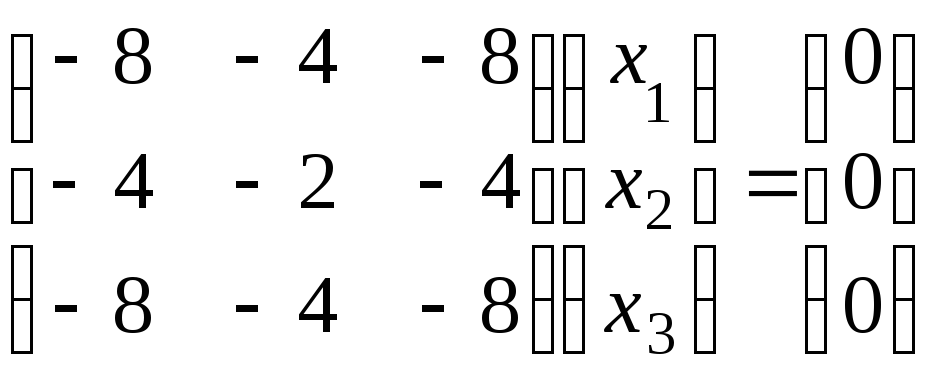
Решая полученную систему методом Гаусса, получим , гдеипроизвольные числа не равные нулю одновременно.

Аналогично находим, что при любоместь собственный вектор матрицыс собственным значением.