- •Часть 1. Линейная алгебра
- •1.1.2. Линейные операции над матрицами
- •1.1.3. Умножение матриц
- •1.1.4.Определители
- •Свойства определителей
- •1.1.5. Обратные матрицы
- •1.2. Системы линейных алгебраических уравнений
- •1.2.1. Метод Крамера
- •1.2.2. Матричный метод
- •1.2.3. Метод Гаусса
- •1.3. Ранг матрицы
- •Свойства ранга матрицы
- •1.4. Собственные векторы и собственные значения матрицы
- •Задачи для самостоятельной работы
- •1.5. Примеры использования алгебраического аппарата для классических экономических моделей.
- •Задачи для самостоятельной работы
Свойства определителей
Определитель не меняется при транспонировании.
Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен 0.
Если две строки (два столбца) поменять местами, то определитель меняет знак.
Если элементы какой-либо строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен 0.
Справедливо равенство
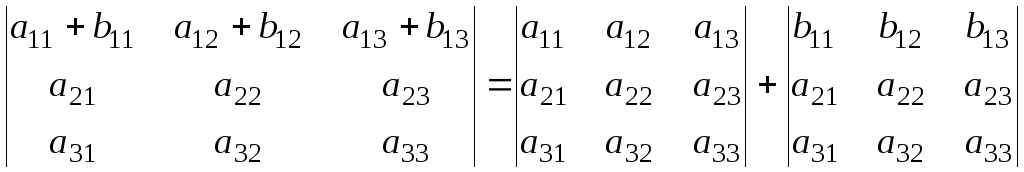 .
.
Определитель не изменится, если к элементам какой-либо его строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.
Сумма произведений элементов любой строки (столбца) на свои алгебраические дополнения равна самому определителю.
Сумма произведений элементов любой строки (столбца) определителя на алгебраические дополнения другой строки (столбца) равна 0.
Теорема
1. Если
![]() и
и![]() – квадратные матрицы
– квадратные матрицы![]() -го
порядка, то
-го
порядка, то
![]() .
.
Следствие.
![]() .
.
Пример
5. (Образец
решения задачи 2 из контрольной работы).
Даны матрицы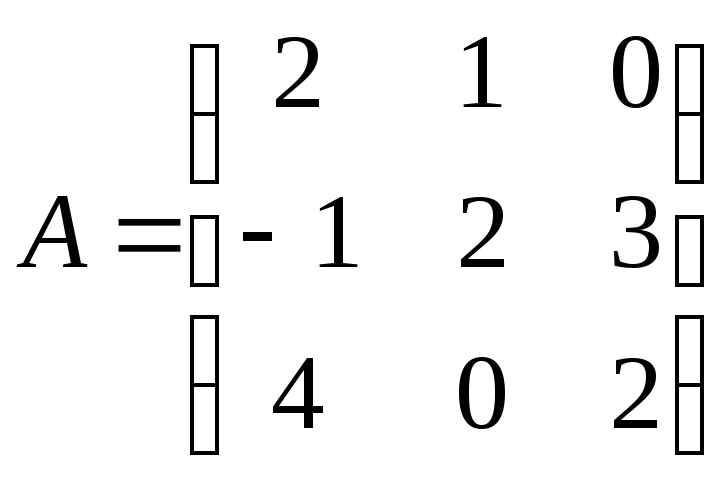 и
и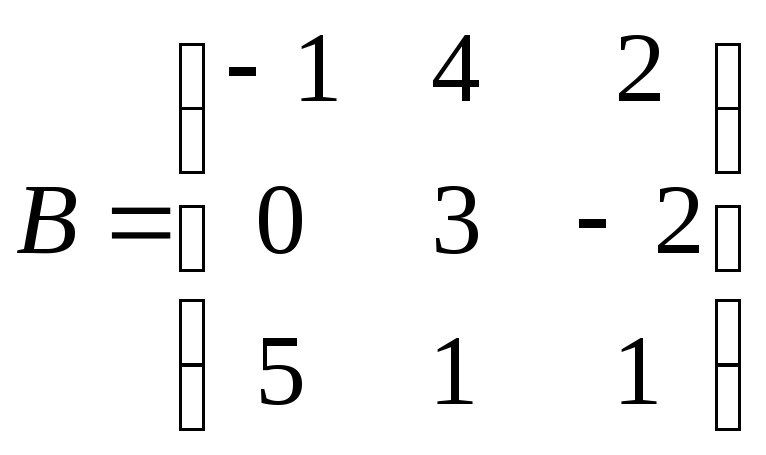 .
Проверить справедливость равенства
.
Проверить справедливость равенства
![]()
![]() .
.
Решение.
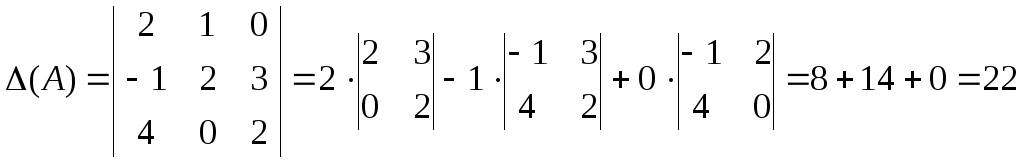
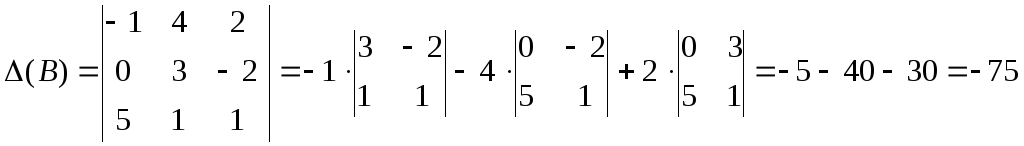
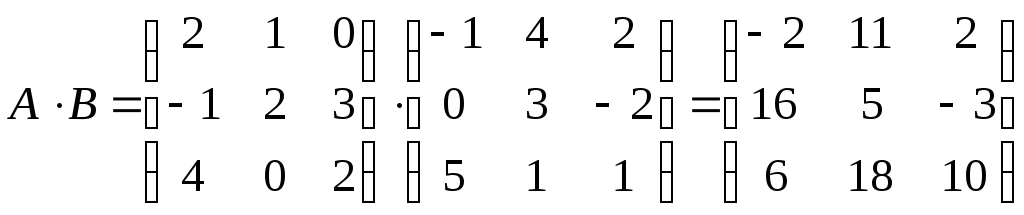
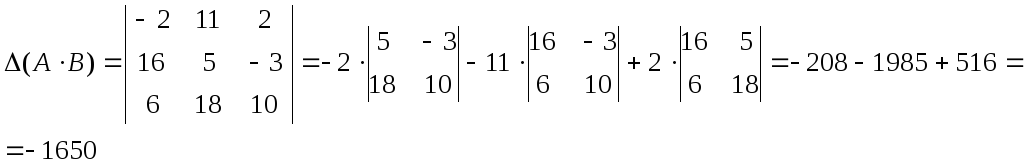
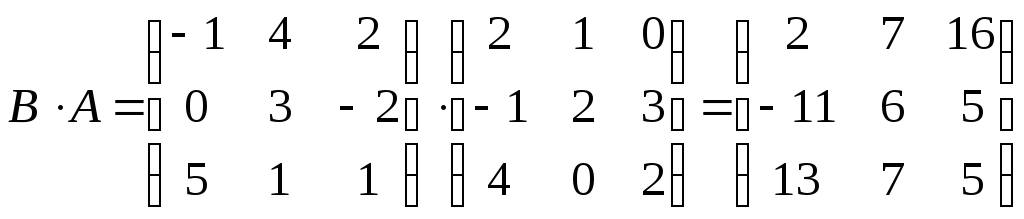
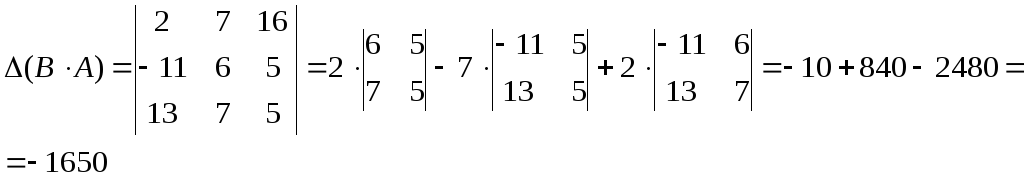
Таким образом,
![]()
![]() =–1650.
n
=–1650.
n
1.1.5. Обратные матрицы
Матрица
![]() называется обратной к квадратной матрице
называется обратной к квадратной матрице![]() ,
если
,
если
![]() .
.
Матрица
![]() называетсявырожденной,
если
называетсявырожденной,
если
![]() ;
в противном случае
;
в противном случае
![]() –невырожденная
матрица.
–невырожденная
матрица.
Для
того, чтобы матрица
![]() имела обратную, необходимо и достаточно,
чтобы она была невырожденной, т.е.
имела обратную, необходимо и достаточно,
чтобы она была невырожденной, т.е.![]() .
.
В таком случае,
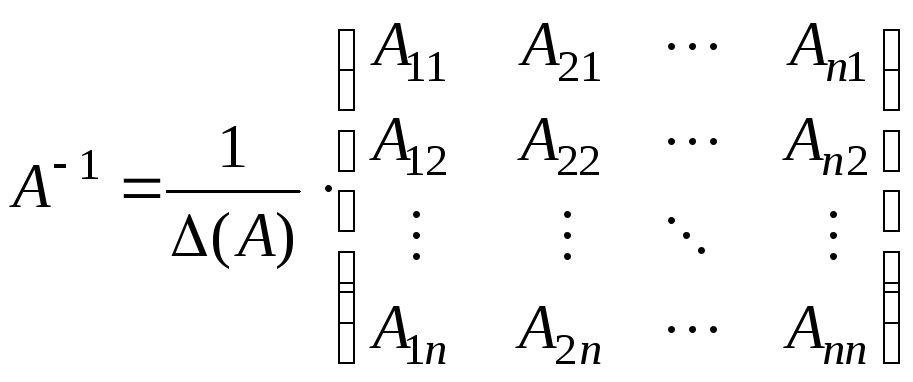 ,
,
т.е.
обратная матрица есть разделенная на
![]() транспонированная матрица алгебраических
дополнений элементов матрицы
транспонированная матрица алгебраических
дополнений элементов матрицы![]() .
.
Пример
6. Дана
матрица
![]()
 .
Найти
.
Найти![]() .
.
Решение.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
и
тогда,
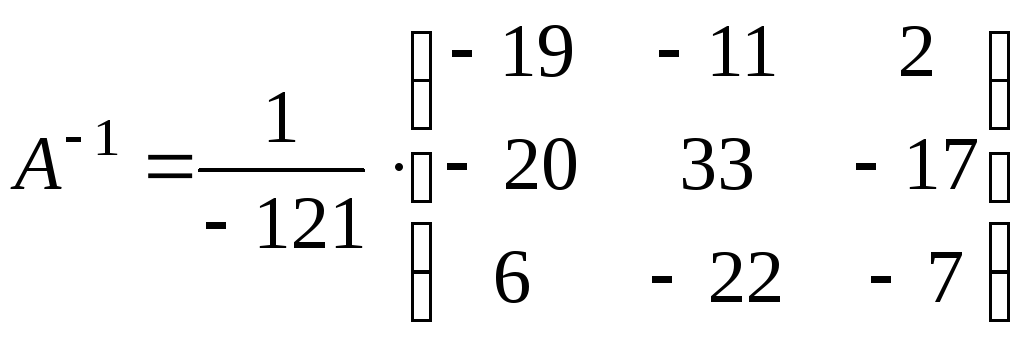 .
.
Проверка.
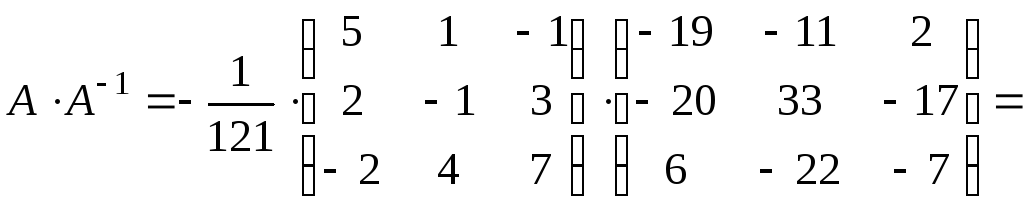
 .
.
Аналогично
убеждаемся, что
![]() .
Значит, матрица
.
Значит, матрица![]() найдена верно.n
найдена верно.n
Справедлива следующая теорема:
Теорема
2. Если
![]() и
и![]() невырожденные квадратные матрицы
одинакового порядка, то
невырожденные квадратные матрицы
одинакового порядка, то
![]() .
.
1.2. Системы линейных алгебраических уравнений
Рассмотрим систему из 3-х алгебраических уравнений с 3-мя неизвестными:
|
|
(1.1) |
1.2.1. Метод Крамера
Теорема 3. Если определитель матрицы системы (1.1)
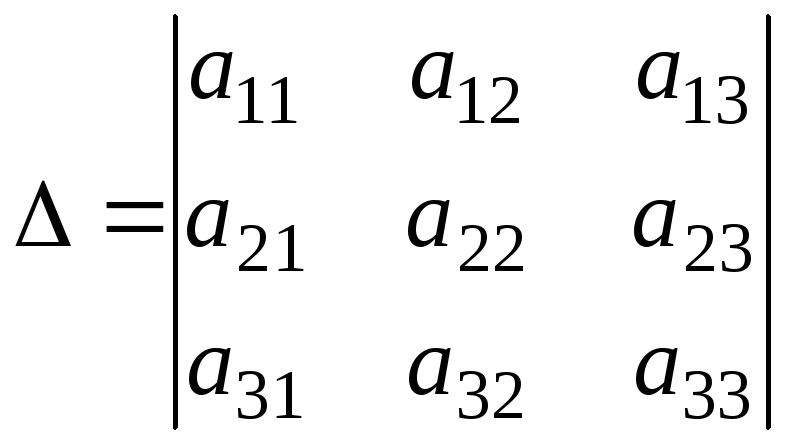
отличен
от нуля (![]() ),
то система имеет единственное решение,
определяемое формулами Крамера:
),
то система имеет единственное решение,
определяемое формулами Крамера:
![]()
где
 ,
,
 ,
,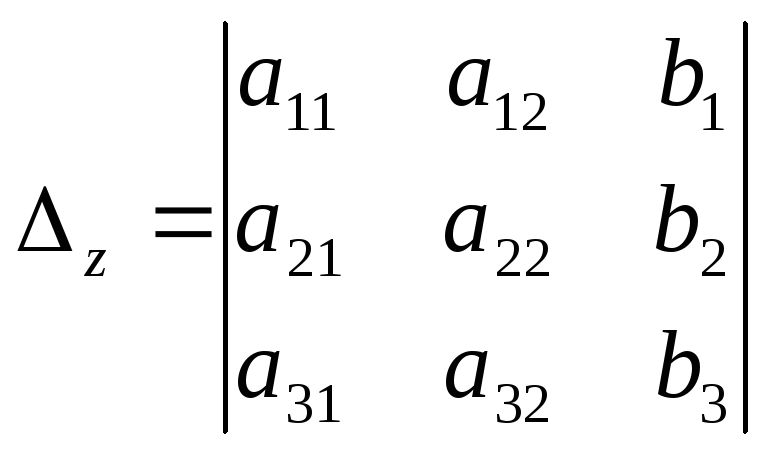 .
.
1.2.2. Матричный метод
Обозначим
через
![]() матрицу системы (1.1), т.е. матрицу,
составленную из коэффициентов при
неизвестных:
матрицу системы (1.1), т.е. матрицу,
составленную из коэффициентов при
неизвестных:
 ,
,
через
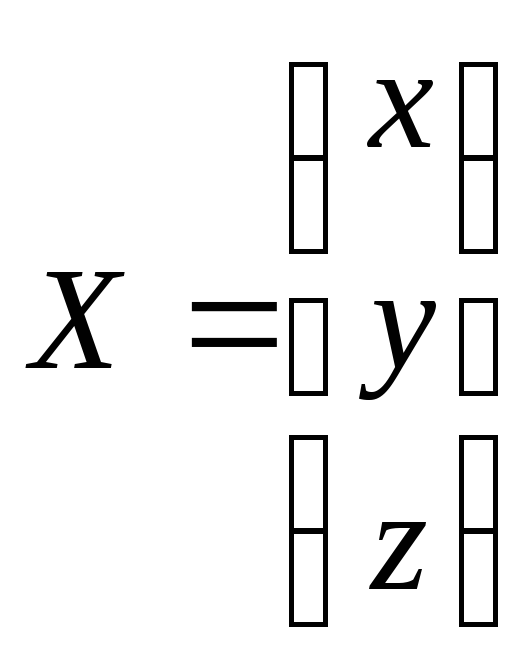 – матрицу-столбец из неизвестных и
через
– матрицу-столбец из неизвестных и
через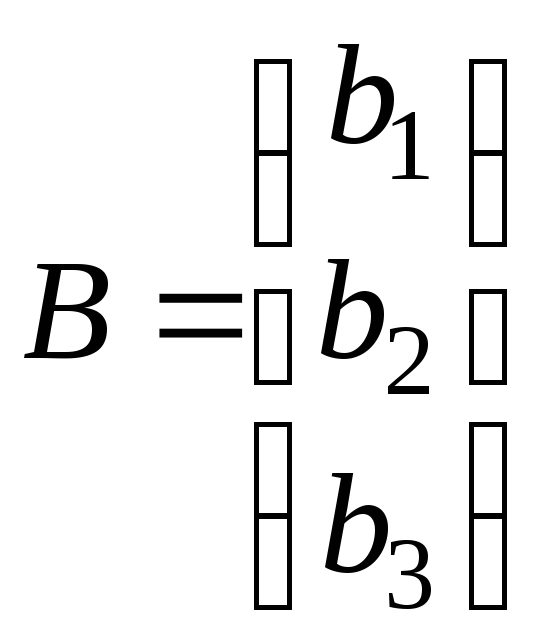 –
матрицу-столбец правых частей.
–
матрицу-столбец правых частей.
Принимая во внимание правило умножения матриц, можно систему линейных уравнений (1.1) записать в виде матричного уравнения:
![]() ,
,
решение которого имеет вид
![]() .
.
Пример 7. (Образец выполнения задачи 1 из контрольной работы) Решить систему уравнений двумя способами:
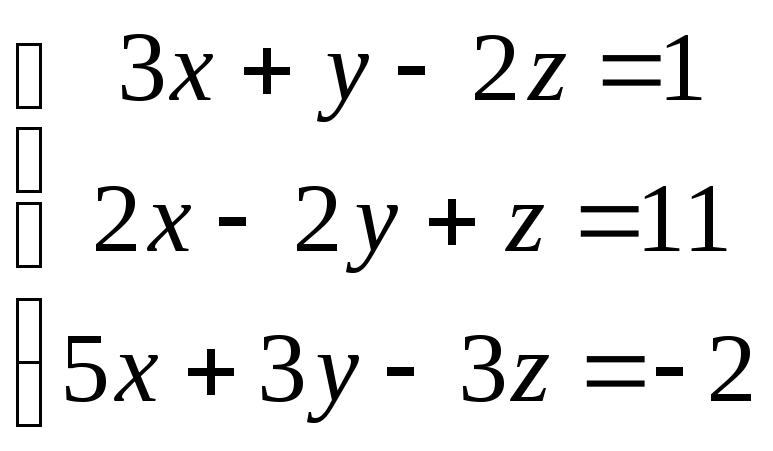 .
.
Решение. Используем метод Крамера:
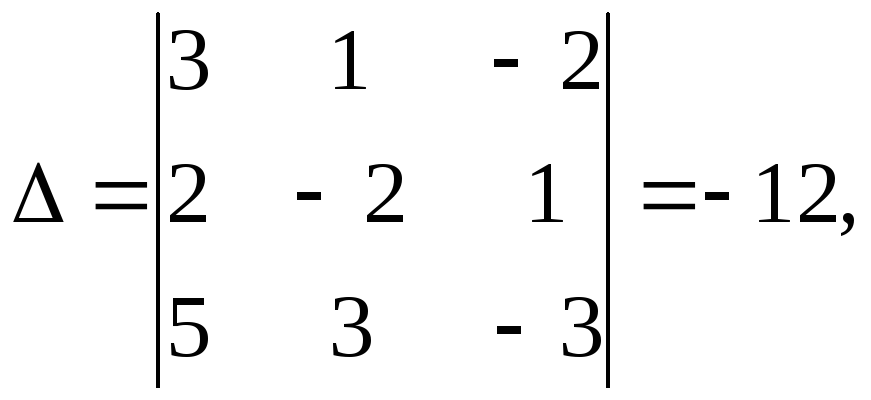
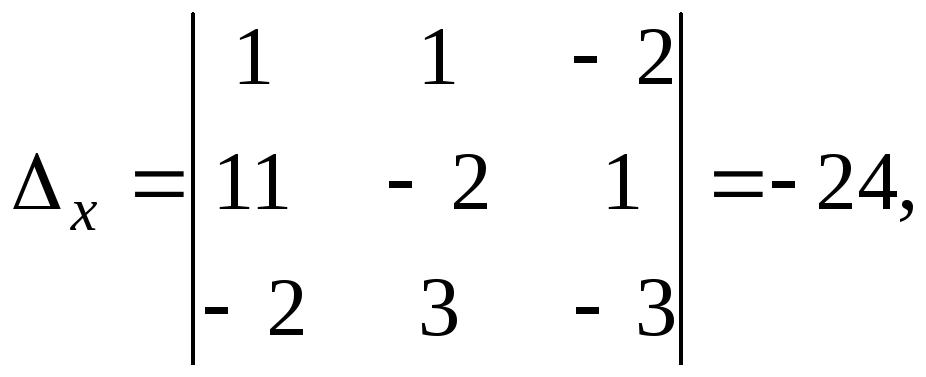
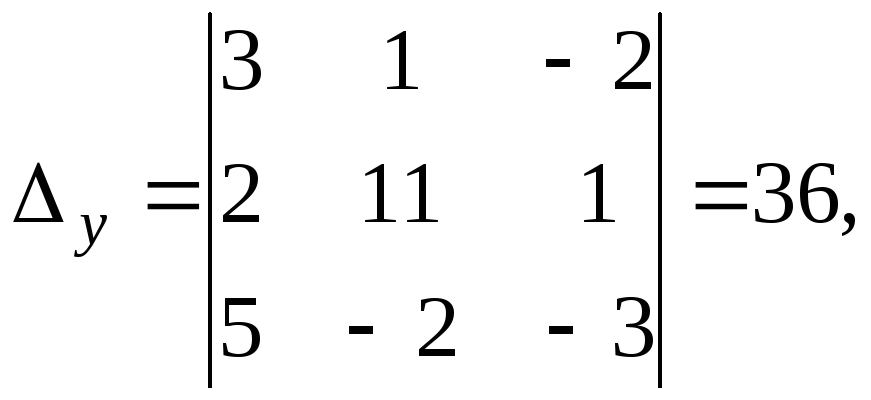
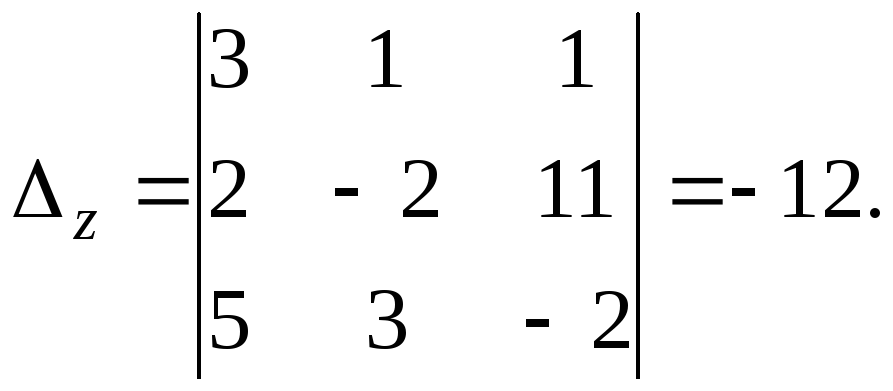
Тогда
![]()
Проверим правильность полученных решений, для чего подставим их в условие:
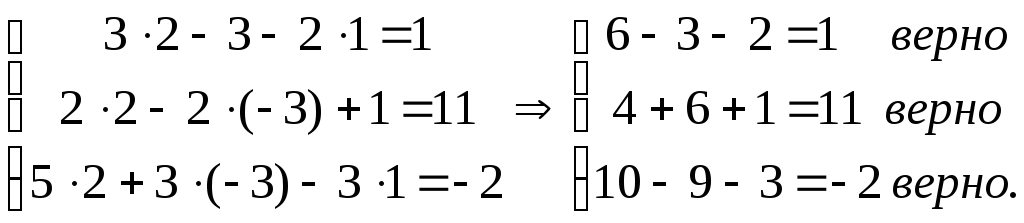
Теперь решим ту же
систему матричным методом. Найдем
обратную матрицу
![]() к матрице системы
к матрице системы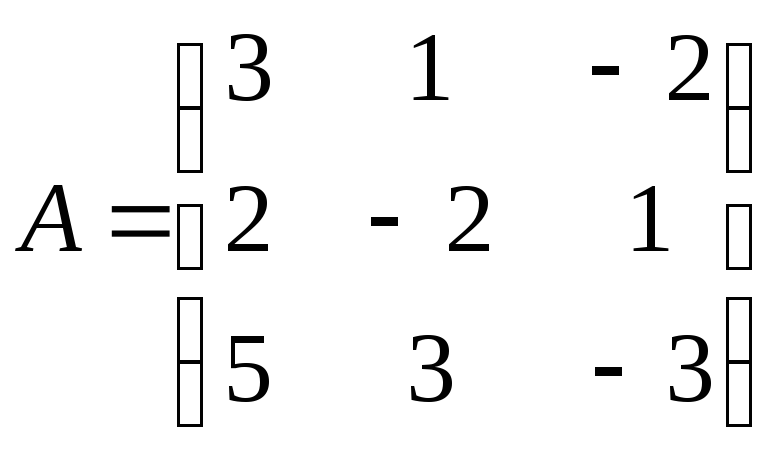 .
Вычислим все алгебраические дополнения:
.
Вычислим все алгебраические дополнения:
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Определитель
матрицы найден выше (фактически это
![]() )
и равен -12.
)
и равен -12.
Следовательно,
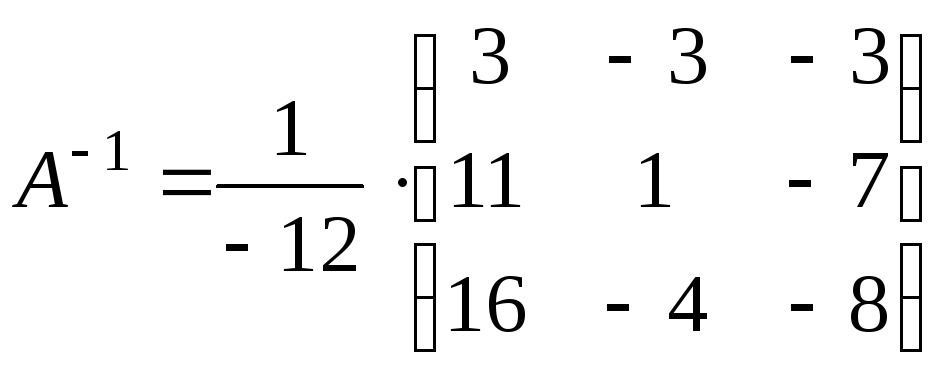 .
Тогда
.
Тогда
 .
.
Ответ:
![]() .n
.n
Замечание 1.Метод Крамера и матричный метод применимы для систем любого конечного порядка при двух условиях: количество уравнений совпадает с количеством неизвестных и определитель системы отличен от нуля.
Замечание 2.Если определитель системы равен нулю, то система либо не имеет решений вообще, либо имеет бесконечное множество решений.