Свойства пределов функции.

1. Если

и на некоторой окрестности ,,, то.

2. Если

и на некоторой окрестности ,,, то.

3. Пусть , гдеи- конечные числа. Тогда

5. Признаки существования пределов

Теорема 1. Если , где- конечное число, то на некоторой окрестностифункцияограничена, т.е. существует положительное числотакое, что

Теорема 3. (критерий Коши существования предела). Для того чтобы существовал предел (конечный) , необходимо и достаточно, чтобы функциябыла определена в окрестности, за исключением, быть может, самой точки, и для всякогосуществовала такая окрестность, что, каковы бы не были точки

Односторонние пределы

По определению число называется пределом функциив точкесправа (слева), если она определена на некотором полуинтервале() и для нее существует

для любой указанной последовательности .

Предел справа (слева) функции в точкепринято обозначать так:

Если определена на интервале, то в точкеможет иметь смысл только число, а в точке- только число.

Равенства эквивалентны существованию предела.

6. Бесконечно большие и бесконечно малые функции

Функцию, для которой называется бесконечно большой при.

Функцию, для которой называется бесконечно малой при.

Свойства бесконечно малых величин.

1. Сумма бесконечно малых величин есть бесконечно малая величина.

2. Произведение двух бесконечно малых величин есть бесконечно малая величина.

3. Произведение бесконечно малой величины на константу есть бесконечно малая величина.

Свойство отражает тот факт, что функциюможно записать в виде, гдепри.

Если функции исами бесконечно малые, то символ(по старинной терминологии) означает бесконечно малую, более высокого порядка .

Если функции исуть бесконечно большие, то символ(по старинной терминологии), означает бесконечно большую более высокого порядка .

Кроме того, пишут

и называют функции иэквивалентными (асимптотически равными) при, если выполняется свойство:

Например.

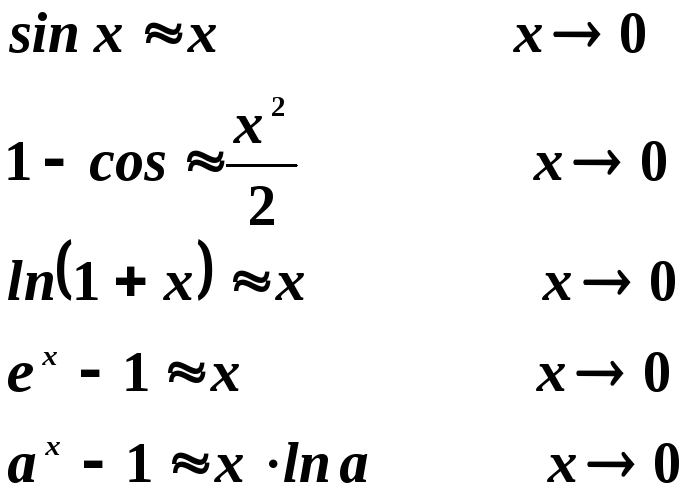
7. Замечательные пределы

1.

Так как функция является непрерывной, топри. Поэтому выражениепредставляет собой неопределенность типа. Предел раскрывает эту неопределенность.

2.

Пример. . Получается из второго замечательного предела заменой.

Пример.

Если , тои

Пример. ,.

Доказательство.

Пример. ,.

Доказательство. Положим . Тогда

8. Непрерывные функции. Определение непрерывности с помощью приращений.

На рисунке изображен график функции. Зададим точку. Близкая ей точка, где- приращение. Разность

называется приращением функции в точке, соответствующим приращению. На рисунке,.

Будем стремить к нулю. Тогда для рассматриваемой функции ибудет стремиться к нулю

Рассмотрим теперь график другой функции . Придадим теперьприращениеи определим соответствующее приращение функции

Если мы будем стремить к нулю, то теперь уже нельзя сказать, чтостремится к нулю.

Теперь можно дать определение.

Функцию , заданную на отрезке, называютнепрерывной в точке этого отрезка, если приращение ее в этой точке, соответствующее приращению, стремится к нулю при любом способе стремленияк нулю.

Это свойство непрерывности в точкезаписывают в виде

В противном случае функция называется разрывной.

Функция непрерывная в любой точке отрезка (интервала), называется непрерывной на этом отрезке (интервале).

Функция называется непрерывной в точке, если она определена в некоторой окрестности этой точки, в том числе и в самой точке, и если ее приращение в этой точке, соответствующее приращению аргумента, стремится к нулю при

Либо ;;

.

Пример. Функция непрерывна для любого. В самом деле.

Но для любого имеет место неравенство. Если, то это следует из рисунка (длина дуги больше стягивающей ее хорды). Отсюда следует

Но тогда, очевидно, . Что и требовалось доказать.

Т. Если функции инепрерывны в точке, то непрерывны также в этой точке их сумма, разность, произведение и частное (при).

Пример. Функция непрерывна. Она является композицией двух непрерывных функций:, и.