1. Параметры уравнения регрессии.

Выборочные средние. Выборочные дисперсии:

Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно:

Коэффициент корреляции

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < r_xy < 0.3: слабая; 0.3 < r_xy < 0.5: умеренная; 0.5 < r_xy < 0.7: заметная; 0.7 < r_xy < 0.9: высокая; 0.9 < r_xy < 1: весьма высокая; В нашем примере связь между признаком Y фактором X высокая и прямая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: Уравнение регрессии (оценка уравнения регрессии). Линейное уравнение регрессии имеет вид y = 0.54 x + 75.82 Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент регрессии b = 0.54 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.54. Коэффициент a = 75.82 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая. Коэффициент эластичности. Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х. Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты. Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения. Коэффициент эластичности находится по формуле: Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно. Ошибка аппроксимации. Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических: Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. 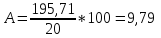Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве регрессии. Коэффициент детерминации. Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака. Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. R²= 0.841² = 0.7072 т.е. в 70.72 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 29.28 % изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации). Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)

x	y	y(x)	(yi-ycp)2	(y-y(x))2	(xi-xcp)2	|y - yx|:y
913	596	566.54	22425.06	868.11	50086.44	0.0494
1095	417	664.36	855.56	61185.18	164673.64	0.59
606	354	401.53	8510.06	2259.32	6922.24	0.13
876	526	546.65	6360.06	426.42	34894.24	0.0393
1314	934	782.06	237900.06	23084.89	390375.04	0.16
593	412	394.55	1173.06	304.67	9254.44	0.0424
754	525	481.08	6201.56	1929.12	4199.04	0.0837
528	367	359.61	6280.56	54.62	25985.44	0.0201
520	364	355.31	6765.06	75.52	28628.64	0.0239
539	336	365.52	12155.06	871.53	22560.04	0.0879
540	409	366.06	1387.56	1843.92	22260.64	0.1
682	452	442.38	33.06	92.54	51.84	0.0213
537	367	364.45	6280.56	6.52	23164.84	0.00696
589	328	392.4	13983.06	4146.75	10040.04	0.2
626	460	412.28	189.06	2277.03	3994.24	0.1
521	380	355.85	4389.06	583.36	28291.24	0.0636
626	439	412.28	52.56	713.87	3994.24	0.0609
521	344	355.85	10455.06	140.35	28291.24	0.0344
658	401	429.48	2047.56	811.16	973.44	0.071
746	514	476.78	4590.06	1385.44	3226.24	0.0724
13784	8925	8925	352033.75	103060.32	861867.2	1.97

2. Оценка параметров уравнения регрессии. Значимость коэффициента корреляции. Выдвигаем гипотезы: H₀: r_xy = 0, нет линейной взаимосвязи между переменными; H₁: r_xy ≠ 0, есть линейная взаимосвязь между переменными; Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H₁ ≠ 0, надо вычислить наблюдаемое значение критерия (величина случайной ошибки) и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы k = n - 2 найти критическую точку t_крит двусторонней критической области. Если t_набл < t_крит оснований отвергнуть нулевую гипотезу. Если |t_набл| > t_крит — нулевую гипотезу отвергают. 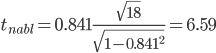По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=18 находим t_крит: t_крит (n-m-1;α/2) = (18;0.025) = 2.101 где m = 1 - количество объясняющих переменных. Если |t_набл| > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). Поскольку |t_набл| > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически значим

В парной линейной регрессии t²_r = t²_b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии. 2.2. Интервальная оценка для коэффициента корреляции (доверительный интервал). Доверительный интервал для коэффициента корреляции.

r(0.573;1)

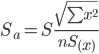
2.3. Анализ точности определения оценок коэффициентов регрессии. Несмещенной оценкой дисперсии возмущений является величина: S² = 5725.573 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). S = 75.67 - стандартная ошибка оценки (стандартная ошибка регрессии). S_a - стандартное отклонение случайной величины a. S_b - стандартное отклонение случайной величины b. 2.4. Доверительные интервалы для зависимой переменной. Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения. Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов. Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bx_p ± ε) где t_крит (n-m-1;α/2) = (18;0.025) = 2.101 Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X_p = 104 Вычислим ошибку прогноза для уравнения y = bx + a y(104) = 0.537*104 + 75.824 = 131.721 131.721 ± 106.33 (25.39;238.05) С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов. Вычислим ошибку прогноза для уравнения y = bx + a + ε (-59.54;322.98)

Доверительный интервал для коэффициентов уравнения регрессии. Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими: (b - t_крит S_b; b + t_крит S_b) (0.54 - 2.101 • 0.0815; 0.54 + 2.101 • 0.0815) (0.366;0.709) С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале. (a - t_крит S_a; a + t_крит S_a) (75.824 - 2.101 • 58.67; 75.824 + 2.101 • 58.67) (-47.435;199.083) С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале. Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента a статистически незначима. 2) F-статистика. Критерий Фишера. Коэффициент детерминации R² используется для проверки существенности уравнения линейной регрессии в целом. Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение с k₁=(m) и k₂=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. где m – число факторов в модели. Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R²=0 на уровне значимости α. 2. Далее определяют фактическое значение F-критерия: где m=1 для парной регрессии. 3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2. F_табл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01. 4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом. Табличное значение критерия со степенями свободы k₁=1 и k₂=18, F_табл = 4.41 Поскольку фактическое значение F > F_табл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством: Дисперсионный анализ. При анализе качества модели регрессии используется теорема о разложении дисперсии, согласно которой общая дисперсия результативного признака может быть разложена на две составляющие – объясненную и необъясненную уравнением регрессии дисперсии. Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной: ∑(y_i - y_cp)² = ∑(y(x) - y_cp)² + ∑(y - y(x))² где ∑(y_i - y_cp)² - общая сумма квадратов отклонений; ∑(y(x) - y_cp)² - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»); ∑(y - y(x))² - остаточная сумма квадратов отклонений.

Источник вариации	Сумма квадратов	Число степеней свободы	Дисперсия на 1 степень свободы	F-критерий
Модель (объясненная)	0	1	0	43.48
Остаточная	103060.32	18	5725.57	1
Общая	352033.75	20-1

Показатели качества уравнения регрессии.

Показатель	Значение
Коэффициент детерминации	0.71
Средний коэффициент эластичности	0.83
Средняя ошибка аппроксимации	9.86