
- •Содержание
- •Глава 1. Кинематика……………………………………………
- •Глава 2. Динамика материальной точки……………….
- •Глава 3. Момент импульса. Динамика твердого тела………
- •Глава 4. Неинерциальные системы отсчета и гравитационное поле……………………………………………………………….
- •Глава 5. Колебания и волны…………………………………..
- •Введение
- •Рекомендации
- •Используемые обозначения
- •Изучаемый материал. Механика.
- •Глава 1. Кинематика
- •Глава 2. Динамика материальной точки.
- •Консервативные и неконсервативные силы. Закон сохранения энергии
- •Глава 3. Момент импульса. Динамика твердого тела
- •Глава 4. Неинерциальные системы отсчета и гравитационное поле.
- •Глава 5:Колебания и волны.
- •1. Система отсчета – это:
- •3. Радиус-вектор – это:
- •3. Момент импульса. Динамика твёрдого тела.
- •1. Момент импульса это:
- •2. Вектор момента импульса :
- •4. Момент импульса равен:
- •6. Единицы измерения момента импульса в системе си:
- •18. Если на маховик, момент инерции которого действует момент сил , то маховик вращается с угловым ускорением:
- •19. К ободу маховика диаметром приложена касательная сила . Если маховик вращается с угловым ускорением , то его момент инерции равен:
- •22. Если масса цилиндра , а радиус , то его момент инерции относительно оси равен:
- •26. Проекция момента импульса на неподвижную ось твёрдого тела, вращающегося с угловой скоростью равна:
- •4. Неинерционные системы отсчёта и гравитационное поле.
- •1.Согласно закону Всемирного тяготения сила гравитационного притяжения f зависит от расстояния по формуле:
- •5. На высоте (- радиус Земли) напряжённость гравитационного поля Земли равна ( - ускорение свободного падения у поверхности Земли):
- •6. Модуль напряжённости гравитационного поля планеты массы на расстоянии от её центра равняется ( - гравитационная постоянная):
- •7.Какое утверждение выполняется с большей степенью точности? Ускорение свободного падения :
- •9. Если в поднимающемся вверх с ускорением лифте находится тело массой , то вес этого тела будет:
- •5. Колебания и волны.
- •12. Период малых колебаний математического маятника равен . Если его поместить в лифт, опускающийся с ускорением (направленным вниз) , то колебания будут происходить с частотой:
- •25. Если -собственная частота колебаний, -частота изменения вынуждающей силы, -затухание, то вынужденные колебания происходят с частотой:
- •34. Если волна распространяется по закону (здесь и в метрах, а в секундах), то длина волны равна:
- •2. Динамика материальной точки.
- •3. Момент импульса. Динамика твердого тела.
- •4. Неинерциальные системы отсчета и
- •5. Колебания и волны.
Изучаемый материал. Механика.
Глава 1. Кинематика
Материальной точкой мы можем считать любое тело, размеры которого не влияют на характер его движения.
Абсолютно твердое тело это тело, у которого в процессе движения расстояние между двумя любыми точками не изменяется.
Движение – изменение положения тела в пространстве.
Положение тела в пространстве и его движение может быть задано только относительно других тел
Система отсчета – система координат, связанная с взаимно неподвижными телами, дополненная способом отсчета времени.
Радиус-вектор. Путь. Перемещение.
|
Рис 1
|
Положение
тела в пространстве
задается радиус-вектором в выбранной
нами системе
отсчета. Например:
Траектория – совокупность точек в пространстве, которые последовательно занимает движущееся тело. Путь (s) –расстояние, пройденное телом по траектории.
|
Скорость. Мгновенная скорость. Средняя скорость
![]() -
мгновенная скорость
-
мгновенная скорость
![]() ,
,
![]() .
.
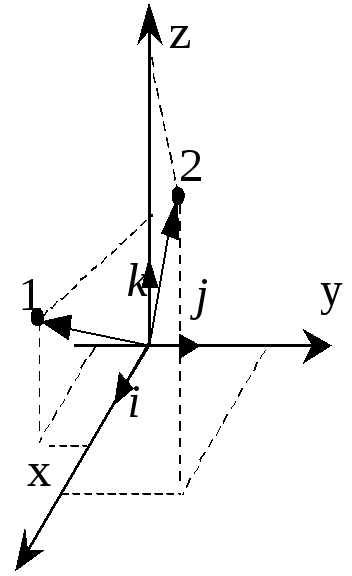
нахождение
модуля скорости по известным проекциям:
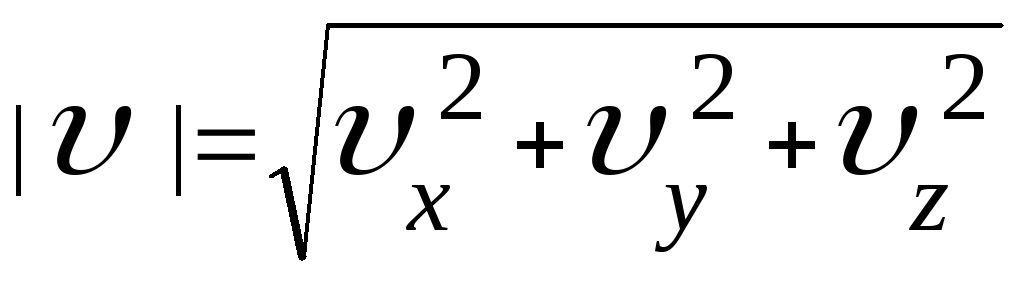
|
Модуль вектора мгновенной скорости можно найти также по зависимости пути от времени, так как при
|
Рис 2
|
Если
за время
![]() перемещение материальной точки будет
равно
перемещение материальной точки будет
равно![]() ,
а пройденный при этом путь равен
Δs,
то
,
а пройденный при этом путь равен
Δs,
то
![]() -средний
вектор скорости,
а
-средний
вектор скорости,
а
![]() -средняя
скорость
за время
-средняя
скорость
за время
![]() .
.
Нахождение пути, перемещения и радиус-вектора по скорости.
Решение
обратной задачи, а именно, нахождение
перемещения
![]() ,
путиs12
и
радиус-вектора
,
путиs12
и
радиус-вектора
![]() по известной скорости требует
применения математической задачи,
обратной взятию производной, то есть
интегрирования:
по известной скорости требует
применения математической задачи,
обратной взятию производной, то есть
интегрирования:
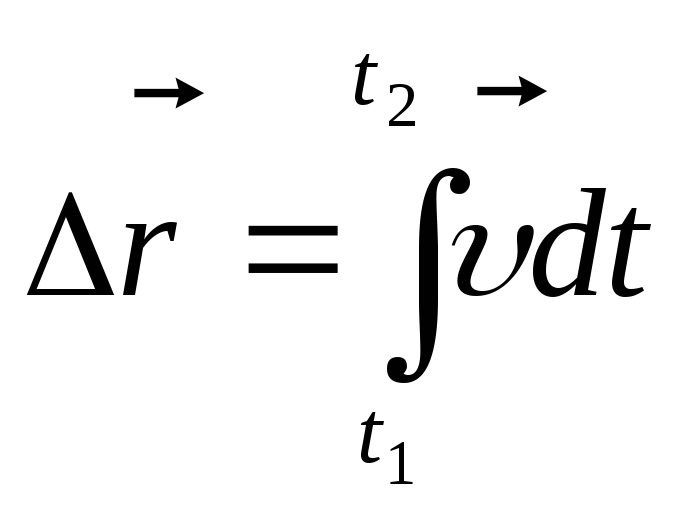
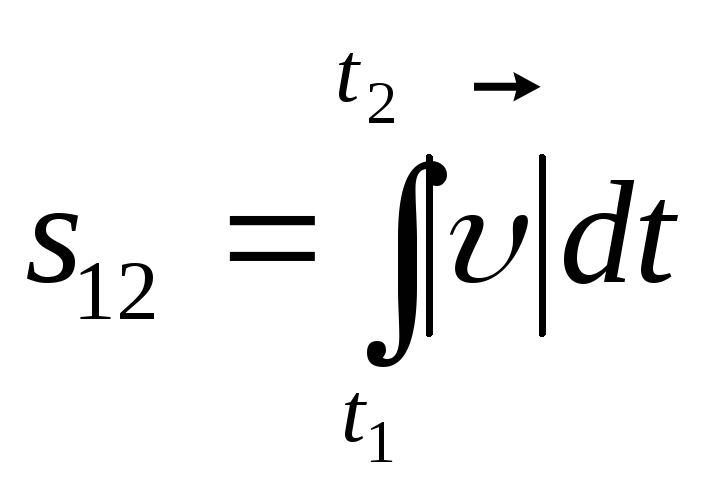 .
.
![]() .
.
Постоянная С находится из начальных условий.
Ускорение.
Ускорение
говорит о том, как быстро меняется
скорость. Мгновенное
(полное) ускорение:
![]()
Скорость
величина векторная, направленная по
касательной к траектории. У нее может
меняться как модуль, так и направление.
Если представим вектор скорости в
виде произведения модуля
![]() и единичного вектора
и единичного вектора![]() (направленного по касательной к
траектории):
(направленного по касательной к
траектории):![]() ,
то при взятии производной получим
два слагаемых:
,
то при взятии производной получим
два слагаемых:
 ,
,
каждое из которых имеет свой физический смысл.
Тангенциальное ускорение
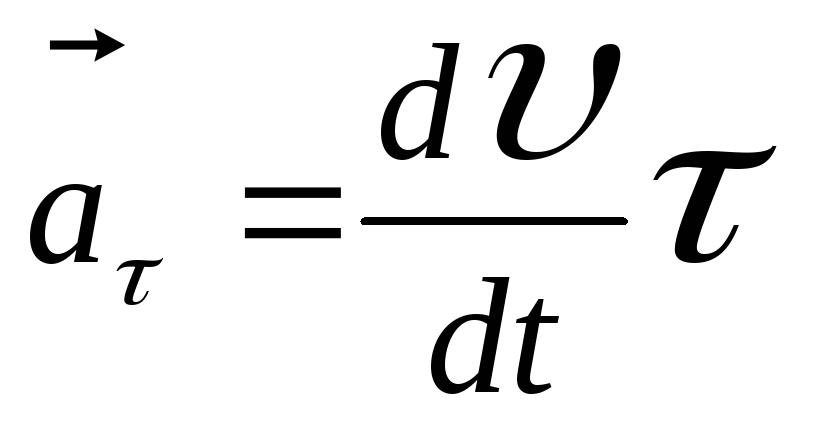
показывает, как быстро меняется модуль скорости. Модуль тангенциального ускорения:
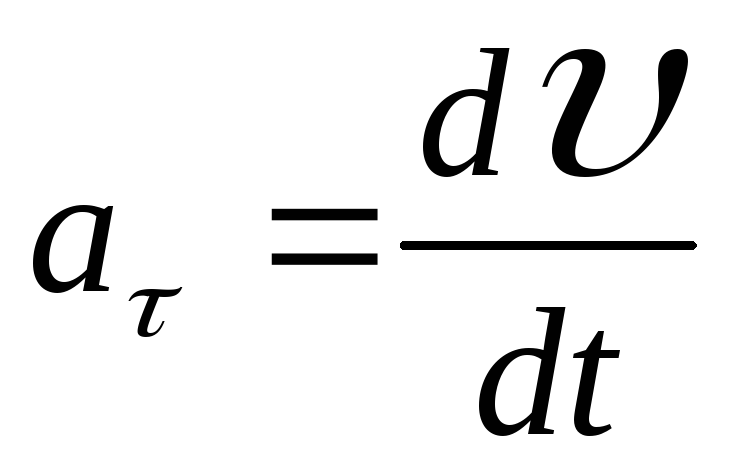 .
.
Нормальное ускорение

показывает, как быстро меняется направление скорости. Модуль нормального ускорения может быть сосчитан по формуле
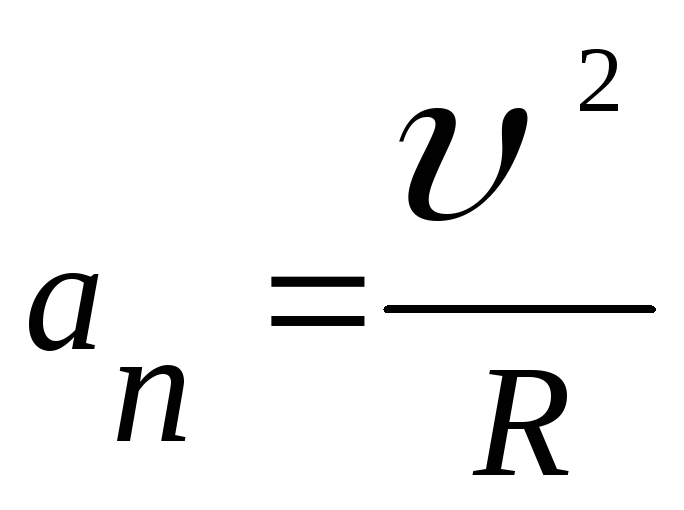 ,
,
где R - радиус кривизны траектории. Направлено нормальное ускорение по нормали (то есть перпендикулярно) к траектории:
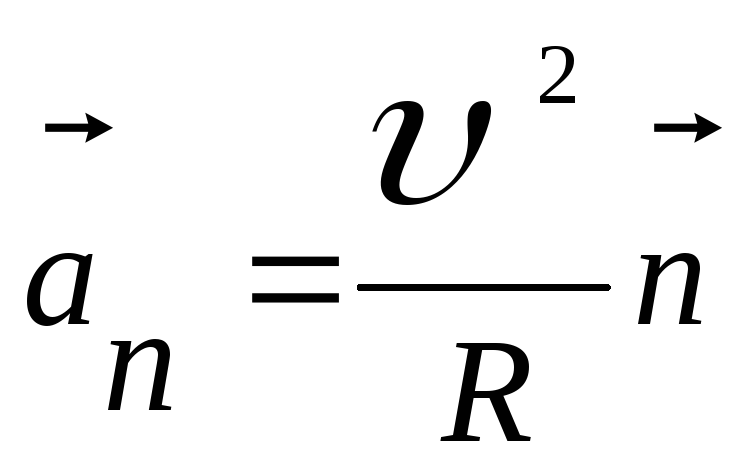 ,
,
здесь
![]() - единичный вектор нормали.
- единичный вектор нормали.
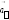 Полное
ускорение
Полное
ускорение
![]() представляет
собой сумму двух ускорений. Тангенциальное
и нормальное ускорения взаимно
перпендикулярны и поэтому модуль
полного ускорения a
связан с
их модулями формулой:
представляет
собой сумму двух ускорений. Тангенциальное
и нормальное ускорения взаимно
перпендикулярны и поэтому модуль
полного ускорения a
связан с
их модулями формулой:
|
Итак,
зная
|
Рис.3. Полное нормальное и тангенциальное ускорения. |
Вращательное движение
|
Рис.5. Вращение. Вектора
|
При
вращении твердого тела две разные
точки его (на расстоянии Rа
и Rв
от центра) за время
Таким образом угол поворота будет являться характеристикой вращательного движения для всего тела в целом. Скорость
вращения (угловая скорость) может
быть найдена с помощью операции
взятия производной.
|
Угловое
ускорение
![]() и угол поворота связаны с угловой
скоростью соотношениями аналогичным
тем, что используются при описании
поступательного движения:
и угол поворота связаны с угловой
скоростью соотношениями аналогичным
тем, что используются при описании
поступательного движения:![]() ,
,![]() .
.
Аналогия записи поступательного и вращательного движения и взаимосвязь между ними
|
Поступательное
s |
Вращательное
|
Взаимосвязь
|
|
|
|
|
|
|
|
|
|
|
|
|

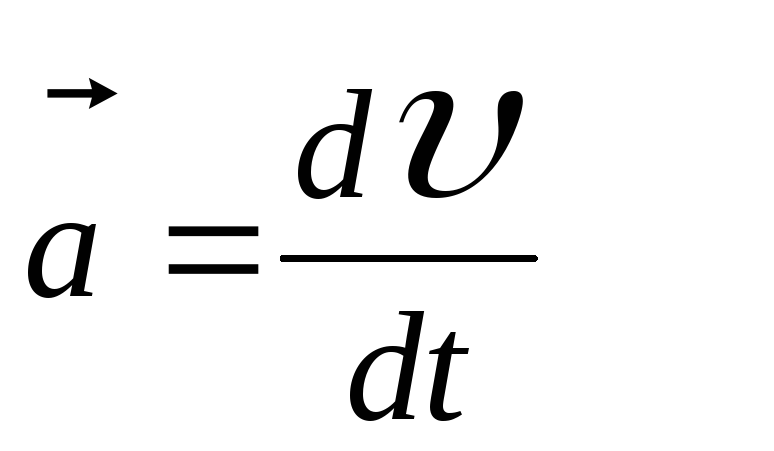 Зная
Зная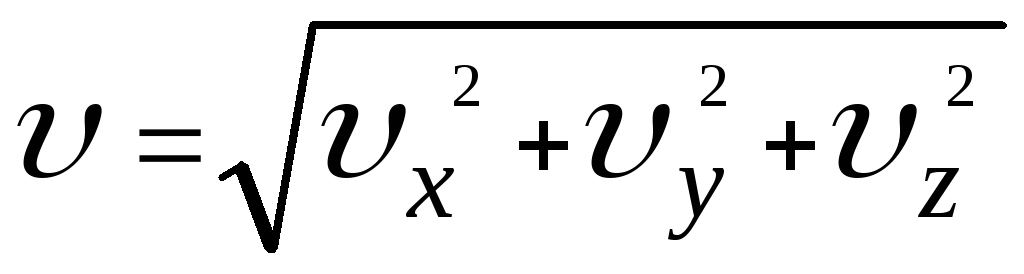 можно найти
можно найти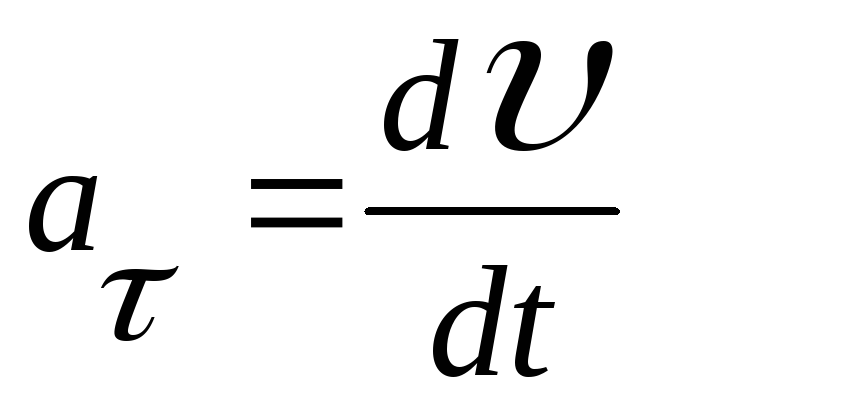 и
и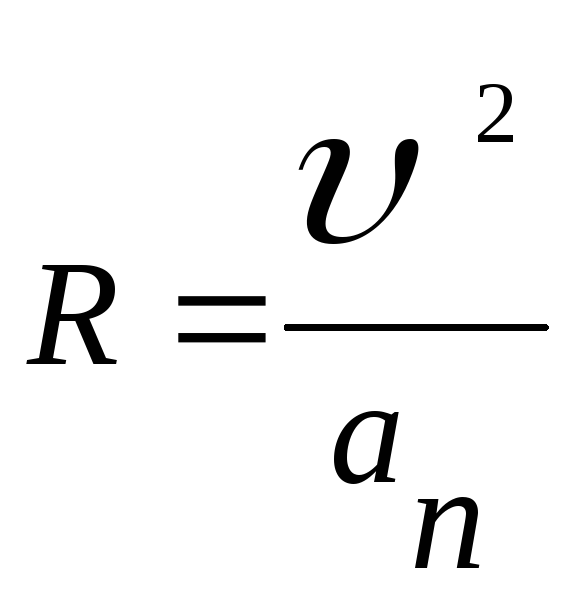

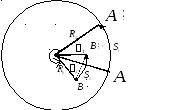
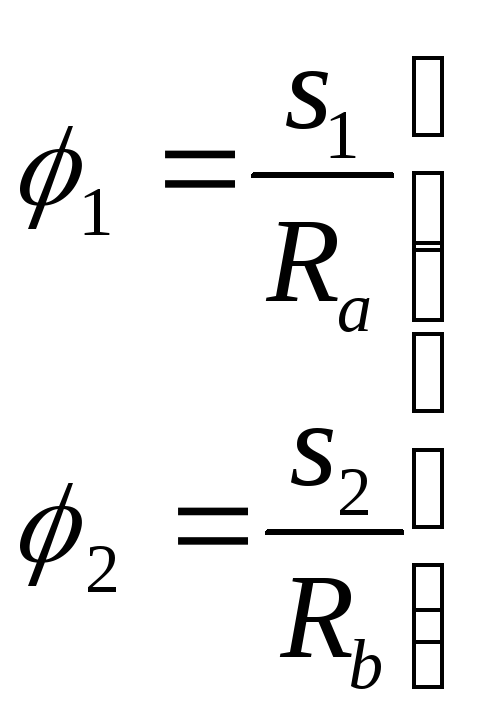 за
время
за
время