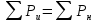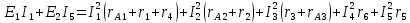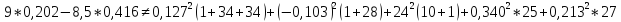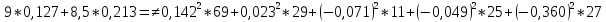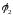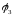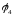Отчёт по расчётно-экспериментальной работе №1
.docxФедеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
Кафедра: Теоретические основы электротехники
ИССЛЕДОВАНИЕ И РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Расчетно-экспериментальная работа №1
Студент группы 41Е:
_________ Г. В. Макаров
Руководитель:
_________А. Г. Зверев
Омск 2012
Цель работы:
1) Освоение методики измерения токов, напряжений, потенциалов.
2) Опытная проверка законов Кирхгофа и принципа наложения.
3) Расчет токов в ветвях заданной электрической цели методами контурных токов, узловых потенциалов, эквивалентного генератора.
4) Построение потенциальной диаграммы.
5) Составление баланса мощностей.
6) Сравнение результатов опыта и расчета.
Исходные данные:
1.
Таблица 1 - Параметры исследуемой цепи
|
Значение ЭДС, В |
Сопротивление резисторов, Ом |
Сопротивление амперметров, Ом |
||||||||||
|
Е1 |
Е2 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
RA1 |
RA2 |
RA3 |
||
|
9 |
8.5 |
34 |
28 |
10 |
34 |
27 |
25 |
1 |
1 |
1 |
||
2.
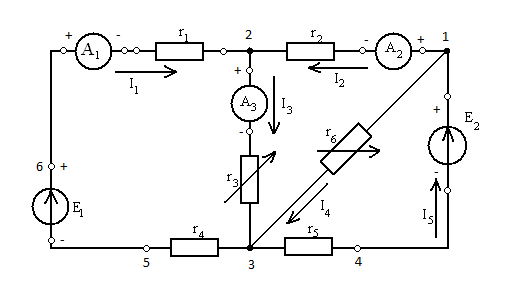
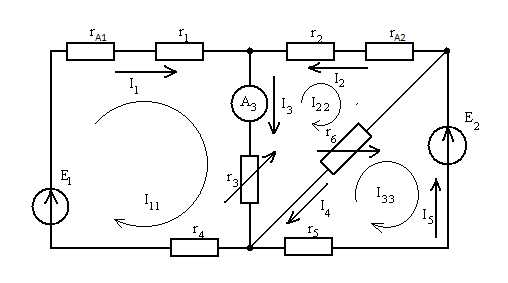
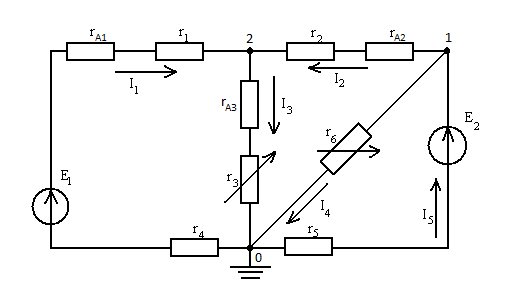
Рисунок 1 – Схема исследуемой цепи.
Описание лабораторной установки
Лабораторная установка содержит:
I)
панель, на которой установлены приборы
магнитоэлектрической системы: три
миллиамперметра и вольтметр, сопротивления
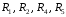 ;
;
2) два источника постоянной регулируемой ЭДС;
3)
два магазина сопротивлений -
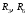 ;
;
4) ключ S, соединительные провода.
Схема
исследуемой цепи, величины
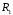 ,
,
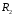 ,
,
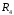 ,
,
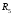 ,
,
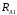 ,
,
 ,
,
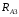 приведены на панели. Величины
приведены на панели. Величины
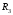 ,
,
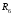 ,
,
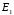 ,
,
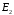 задаются
преподавателем. Сопротивления источников
питания в расчетах принимают равным
нулю, поскольку их величины на несколько
порядков меньше, чем сопротивления
задаются
преподавателем. Сопротивления источников
питания в расчетах принимают равным
нулю, поскольку их величины на несколько
порядков меньше, чем сопротивления
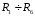 которые
равны десяткам Ом. Вольтметр можно
считать идеальным (
которые
равны десяткам Ом. Вольтметр можно
считать идеальным (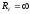 ),
так как его сопротивление на несколько
порядков больше, чем
),
так как его сопротивление на несколько
порядков больше, чем
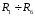 .
.
Таблица 2 - Сравнение значений токов, полученных в расчёте и в опыте
|
Токи в ветвях, мА |
Способ определения значения тока |
||||||
|
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
|
|
|
100 |
60 |
160 |
|
|
|
Опытным путём |
|
|
105 |
-55 |
50 |
-85 |
190 |
|
Методом контурных токов |
|
|
142 |
23 |
-71 |
-49 |
-360 |
|
Методом узловых потенциалов |
|
|
|
|
|
|
|
|
Методом эквивалентного источника |
|
Таблица 3 - Сравнение значений потенциалов, полученных расчетом и в опыте
|
Потенциалы точек цепи, В |
Способ определения |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опытным путем |
|
|
|
|
|
|
|
|
Методом узловых потенциалов |
|
Таблица 4 – проверка принципа наложения.
|
Включены ЭДС, В |
Токи, мА |
|||||
|
Опыт |
Расчёт |
|||||
|
E1 |
I1' |
I2' |
I3' |
Преобразованием цепи |
||
|
I1' |
I2' |
I3' |
||||
|
120 |
20 |
110 |
|
|
|
|
|
E2 |
I1'' |
I2'' |
I3'' |
Преобразованием цепи |
||
|
I1'' |
I2'' |
I3'' |
||||
|
10 |
90 |
75 |
|
|
|
|
|
E1, E2 |
I1 |
I2 |
I3 |
Методом наложения |
||
|
I1 |
I2 |
I3 |
||||
|
100 |
50 |
150 |
|
|
|
|
Расчетная часть.
1.
Составить уравнения по первому и второму
законам Кирхгофа. Убедиться, что при
подстановке в них значений измеренных
токов получаются тождества (проверить
уравнения с токами
 ,
,
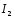 ,
,
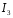 )
)
Первый закон Кирхгофа формулируется для узла электрической цепи:
алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю. При этом подходящие к узлу токи записываются с одним знаком, отходящие — с другим.
Согласно этому закону можно записать систему
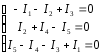
Подставим
измеренные токи
 в первое уравнение:
в первое уравнение:
-I1 - I2+I3= - 0.1 - 0.06+0.16=0
Второй закон Кирхгофа формулируется для контура электрической цепи:
алгебраическая сумма падений напряжений на участках контура равна алгебраической сумме ЭДС того же контура. При этом, если направление ЭДС совпадает с направлением. обхода контура, то она берется со знаком плюс, а если не совпадает — со знаком минус. Падение напряжения на элементе берется со знаком плюс, если направление тока в элементе совпадает с направлением обхода, если не совпадает — со знаком минус.
В данной схеме три контура, следовательно согласно второму закону Кирхгофа получится три уравнения:
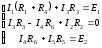
Подставим
измеренные токи
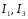 в первое уравнение:
в первое уравнение:
0,1(34+34)+0,16*(10)
=8,66≈Е1.
Учитывая погрешности при измерении
токов
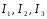 видно, что тождество выполняется.
видно, что тождество выполняется.
Введем некоторые упрощения в схему:
R1=R1+RA1=35 Ом
R2=R2+RA2=29 Ом
R3=R3+RA3=11 Ом
2) Построить потенциальную диаграмму для внешнего контура (по данным опыта).
Распределение
потенциалов вдоль неразветвленной цепи
можно представить в виде графика. Мы
будем проводить исследования внешнего
контура заданной схемы. Будем двигаться
по контуру по часовой стрелке начиная
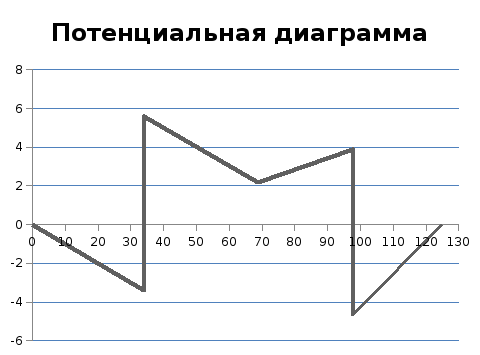
с потенциала
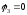 B
B
𝜑5 = 𝜑3 – I1R4 = -3.4 B
𝜑6 = 𝜑5 + E1 = 5.6 B
𝜑2 = 𝜑6 – I1R1 = 2.2 B
𝜑1 = 𝜑2 + I2R2 = 3.88 B
𝜑4 = 𝜑1 – E2 = - 4.62 B
𝜑3 = 𝜑4 + I5R5 = 0
|
Координаты |
Точки контура |
||||||
|
3 |
5 |
6 |
2 |
1 |
4 |
3 |
|
|
x, Ом |
0 |
34 |
34 |
69 |
98 |
98 |
125 |
|
у, В |
0 |
-3.4 |
5.6 |
2.2 |
3.88 |
-4.62 |
0 |
3) Рассчитать и занести в таблицу 4 токи от действия каждой ЭДС в отдельности, используя преобразование схемы.
I.
Отключив ЭДС
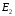 найдем токи в цепи:
найдем токи в цепи:
1. Находим общее сопротивление:
R56
=
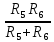 = 12.98 Ом
= 12.98 Ом
R256 = R56 + R2 = 41.98 Ом
R2356
=
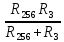 = 8.71 Ом
= 8.71 Ом
R = R1 + R4 + R2356 = 78.71Ом
2. Найдём общий ток в цепи:
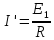 =
0.114 А
=
0.114 А
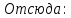
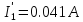
U23 = I1'
Расчёт методом контурных токов
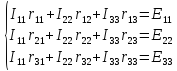
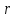 11=rA1+r1+rA3+r3+r4=1+34+1+10+34=80
11=rA1+r1+rA3+r3+r4=1+34+1+10+34=80
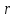 22=rA2+r2+rA3+r3+r6=1+28+1+10+25=65
22=rA2+r2+rA3+r3+r6=1+28+1+10+25=65
r33=r6+r5=27+25=52
r12=r21=-(rA3+r3)=-1-10=-11
r13=r31=0
r23=r32=r6=-25
E11=E1=9
E22=0
E33=-E2=-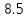
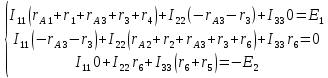
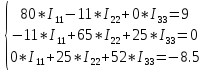
Δ=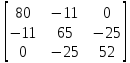 =214108
=214108
Δ1=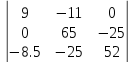 =22457,5
=22457,5
Δ2=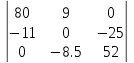 =-11852
=-11852
Δ3=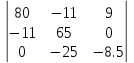 =-40696,5
=-40696,5
I11=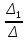 =
= =0.105
=0.105
I22=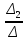 =
=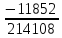 =-0.055
=-0.055
I33=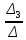 =
=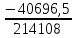 =-0.190
=-0.190
I1=I11=0.105 А = 105 мА
I2=-I22=-0.055 A = -55 мА
I3=I11-I22=0.105-0.055=0.050 A = 50 мА
I4=I22-I33=0.105-0.190=0.085 A = -85 мА
I5=-I33=0.190 A=190 мА
Расчёт методом узловых потенциалов
Узел 1: I5+I4-I2=0
Узел 2: I1+I2-I3=0
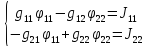
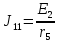 =
=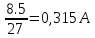
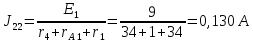
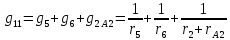 =
=
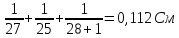
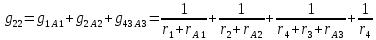 =
=
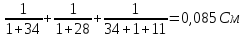
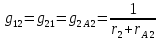 =
=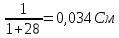
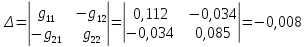
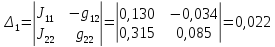

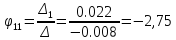 В
В
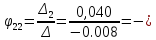 5
В
5
В
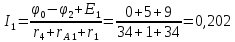 А=202мА
А=202мА
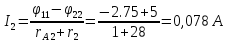
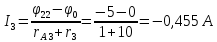
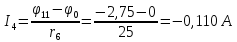
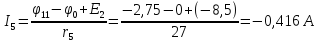
Баланс мощностей