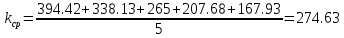Перечень безопасных расстояний при работе с шариковыми разрядниками
Таблица 1:
|
D, cм |
Amin |
Amax |
R |
|
До 6.25 |
7D |
9D |
14S |
|
10 - 15 |
6D |
8D |
12S |
|
25 |
5D |
7D |
10S |
|
50 |
4D |
6D |
8S |
Зависимость значений расстояния между шарами разрядника от напряжения пробоя.
Таблица 2 - Результаты измерений расстояния между шарами от напряжения
|
Расстояние между шарами, см |
Напря-жение на об-мотке авто-транс-форма-тора U1, В |
Коэффи-циент нерав-номер-ности электрического поля, f |
Пробив-ной гра-диент воздуха gпр, кВ/см |
Макси-маль-ное про-бивоне напря-жение Uпр.max, кВ |
Эффек-тивное напря-жение пробоя Uэф.пр.,кВ |
Коэффи-циент транс-форма-ции, k | |||||||||
|
X1 |
X2 |
X3 |
xср |
|
|
|
|
|
| ||||||
|
1 |
1,1 |
1,1 |
1,07 |
50 |
1.06 |
- |
- |
- |
- | ||||||
|
1,3 |
1,3 |
1,3 |
1,3 |
70 |
1,07 |
32,17 |
39,05 |
27,61 |
394,42 | ||||||
|
1,7 |
1,7 |
1,7 |
1,7 |
80 |
1,09 |
32,17 |
38,25 |
27,05 |
338,13 | ||||||
|
2,1 |
2,1 |
2,1 |
2,1 |
100 |
1,12 |
32,17 |
37,47 |
26,50 |
265,00 | ||||||
|
2,5 |
2,5 |
2,5 |
2,5 |
125 |
1,14 |
32,17 |
36,72 |
25,96 |
207,68 | ||||||
|
3,1 |
3,1 |
3,1 |
3,1 |
150 |
1,17 |
32,17 |
35,63 |
25,19 |
167,93 | ||||||
Таблица 3 – Результаты измерений напряжений от расстояния между шарами
|
Расстояние между шарами x, см |
Напряжение на обмотке автотранс-форматора, U2, В |
Коэффи-циент нерав-номер-ности эл. поля, f |
Пробив-ной гра-диент воздуха gпр, кВ/см |
Макси-маль-ное про-бивоне напря-жение Uпр.max, кВ |
Эффек-тивное напря-жение пробоя Uэф.пр.,кВ |
Коэффи-циент транс-форма-ции, k | |||||||
|
измерение | |||||||||||||
|
1 |
2 |
3 |
ср. | ||||||||||
|
4 |
180 |
194 |
192 |
188,67 |
1.23 |
32,17 |
109,98 |
77,77 |
412,2 | ||||
Расчёты
Так как радиус шаров Rш=6,25 см, то диаметр шаров D=2Rш=2*6.25=12.5см.
В лаборатории была температура t=18 0C и барометрическое давление Р=730 мм рт. ст.
Согласно формуле (2) относительная плотность воздуха δ
=
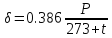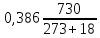=0,97
Формула
(1) выполняется при 0,5
<X<2R
Xmin=0.5
=1.25
см;Xmax=2*6.25=12.5
Xср=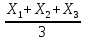
При
U2=50
В, Xср
=
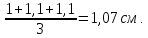НоXср<
Xmin,
то есть Xср<0.5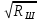
,
что противоречит формуле (3), следовательно
формула (1) не справедлива при заданных
условиях, то есть определить пробивной
градиент gпр
по формуле (1) нельзя.
Соответственно нельзя вычислить амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max по формуле (4), так как для этого надо знать пробивной градиент gпр
Коэффициент неравномерности электрического поля f вычисляется по формуле (5):
f=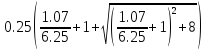
=1.06
Эффективное напряжение пробоя Uэф.пр по формуле (6) и коэффициент трансформации k по формуле (7) вычислить нельзя, так как надо знать амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max.
При
U2=70
В, Xср
=
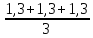=1,3
см. Xmin
< Xcp
< Xmax,
то есть формулу (1) уже можно применить
для расчёта пробивного градиента gпр.
gпр=
= 32.17
Коэффициент неравномерности вычисляется по формуле (5):
f=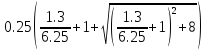
=1,07
Соответственно можно вычислить амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max по формуле (4)
Uпр.max=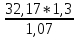
= 39,05 кВ
Эффективное напряжение пробоя Uэф.пр можно вычислить по формуле (6):
Uэф.пр
=
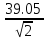= 27.61кВ
Коэффициент трансформации повышающего высоковольтного трансформатора вычисляется по формуле (7):
k
=
=394,42
При U2=80
В, Xср
=
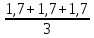=1,7
см. Xmin
< Xcp
< Xmax,
то есть формулу (1) можно применить для
расчёта пробивного градиента gпр.
gпр=
= 32.17
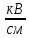
Коэффициент неравномерности вычисляется по формуле (5):
f=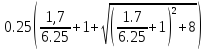
=1,09
Соответственно можно вычислить амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max по формуле (4)
Uпр.max
=
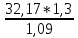= 38,25 кВ
Эффективное напряжение пробоя Uэф.пр можно вычислить по формуле (6):
Uэф.пр
=
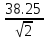= 27.05кВ
Коэффициент трансформации повышающего высоковольтного трансформатора вычисляется по формуле (7):
k
=
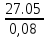=338,13
При
U2=100
В, Xср
=
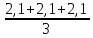=2,1
см. Xmin
< Xcp
< Xmax,
то есть формулу (1) можно применить для
расчёта пробивного градиента gпр.
gпр=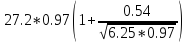
= 32.17
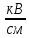
Коэффициент неравномерности вычисляется по формуле (5):
f=
=1,12
Соответственно можно вычислить амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max по формуле (4)
Uпр.max=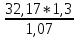
= 37,47 кВ
Эффективное напряжение пробоя Uэф.пр можно вычислить по формуле (6):
Uэф.пр
=
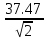= 26,50кВ
Коэффициент трансформации повышающего высоковольтного трансформатора вычисляется по формуле (7):
k
=
=265
При U2=125
В, Xср
=
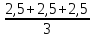=2,5
см. Xmin
< Xcp
< Xmax,
то есть формулу (1) можно применять для
расчёта пробивного градиента gпр.
gпр=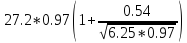
= 32.17
Коэффициент неравномерности вычисляется по формуле (5):
f=
=1,14
Соответственно можно вычислить амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max по формуле (4)
Uпр.max=
= 36,72 кВ
Эффективное напряжение пробоя Uэф.пр можно вычислить по формуле (6):
Uэф.пр
=
= 25.96кВ
Коэффициент трансформации повышающего высоковольтного трансформатора вычисляется по формуле (7):
k
=
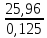=207,68
При U2
=
=188,67
см. Xmin
< Xcp
< Xmax,
то есть формулу (1) уже можно применять
для расчёта пробивного градиента gпр.
gпр=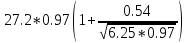
= 32.17
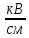
Коэффициент неравномерности вычисляется по формуле (5):
f=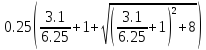
=1,17
Соответственно можно вычислить амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max по формуле (4)
Uпр.max=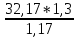
= 35,63 кВ
Эффективное напряжение пробоя Uэф.пр можно вычислить по формуле (6):
Uэф.пр
=
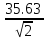= 25,19кВ
Коэффициент трансформации повышающего высоковольтного трансформатора вычисляется по формуле (7):
k
=
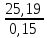=167,93
Теперь
рассчитаем зависимость напряжения
пробоя от расстояния между шарами при
Х=4см и U2=150
В, Xср
=
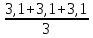=3,1
см и занесём данные в таблицу 3.
gпр=
= 32.17
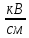
Коэффициент неравномерности вычисляется по формуле (5):
f=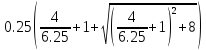
=1,23
Амплитудное (пробивное) напряжение разрядника в момент разряда Uпр.max:
Uпр.max=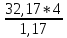
= 109,98 кВ
Эффективное напряжение пробоя Uэф.пр можно вычислить по формуле (6):
Uэф.пр
=
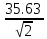= 77,77кВ
Коэффициент трансформации повышающего высоковольтного трансформатора вычисляется по формуле (7):
k
=
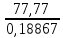=412,2
Определим среднее значение коэффициента трансформации:
