3. Расчет сжатых стержней на Устойчивость

   1. Основные теоретические сведения

Устойчивостью называется способность тела при действии на него внешних нагрузок сохранять первоначальное положение равновесия.

Сила, при превышении которой стержень теряет устойчивость, называется критической силой, обозначается она Р_кр.

Понятие устойчивости связано с характеристикой стержня, получившей название гибкости. Гибкими называют стержни, у которых размеры поперечного сечения значительно меньше длины стержня.

Гибкость стержня определяется по формуле:

(3.1)

где L– длина стержня;

–минимальный размер инерции сечения;

– минимальный момент инерции сечения;

F – площадь сечения.

В реальных условиях существуют несколько вариантов закрепления концов стержней, наиболее распространенные из них представлены на рис. 3.1, где для каждого варианта показана форма потери устойчивости и приведено значение коэффициента закрепления концов стержня .

По значению гибкости принято разделять стержни на три класса. Для каждого класса значение критической силы Р_крвычисляется по определенной формуле.

1) Стержни большой гибкости, > 100.

Критическая сила вычисляется по формуле Эйлера:

(3.2)

где Е – модуль упругости материала.

а б в г

Рис. 3.1. Варианты закрепления стержней

2) Стержни средней гибкости, .

Критическая сила рассчитывается по формуле Ясинского:

(3.3)

где а, b – постоянные, определяемые опытным путем для заданного материала; для стали .

3) Стержни малой гибкости, < 40.

В этом случае стержень не теряет устойчивости и работает в условиях простого сжатия, а критическая сила

, (3.4)

где– предел текучести материалов, для стали

Допускаемая сила в задачах на определение устойчивости должна быть меньше Р_кр:

, (3.5)

где n – коэффициент запаса устойчивости, n > 1.

Допускаемую силу можно вычислять на основании условия устой-чивости:

, (3.6)

где – допускаемое напряжение материала на сжатие;

– коэффициент снижения допускаемого напряжения (), определяется он по справочной таблице.

Зависимость значения коэффициента от гибкости стержня

Гибкость стержня	0	10	20	30	40	50	60	70	80	90	100
Значение для стали Ст3	1	0,99	0,96	0,94	0,92	0,89	0,86	0,81	0,75	0,69	0,60
Гибкость стержня	110	120	130	140	150	160	170	180	190	200
Значение для стали Ст3	0,52	0,45	0,40	0,36	0,32	0,29	0,26	0,23	0,21	0,19

2. Решение типовой задачи

Стальной стержень, длина Lкоторого равна 1 м, сжимается силой Р_кр. Условия закрепления концов стержня показаны на рис. 3.2 (= 2). Определить коэффициент запаса устойчивости n.

Поперечное сечение стержня состоит из четырех неравнобоких уголков 45 × 28 × 3 и прямоугольника с высотой h, равной 12 см, и ширинойb, равной 1,2 см (рис. 3.3).

Решение.

Поскольку сечение дважды симметричное, то оси симметрии z и y являются главными осями составного сечения. Проведем для каждого сечения собственные оси. Для прямоугольного сечения собственные оси z₁, y₁совпадают с главными осями – z, y.

Оси для неравнобокого уголка проходят через его центр тяжести и обозначаются z₂, y₂.

Общее сечение состоит из различных фигур. Определим их геометрические характеристики.

Рассмотрим прямоугольное сечение (рис. 3.4).

Площадь сечения Моменты инерции рассчитаем по формулам:

; (3.7). (3.8)

Рис. 3.3. Поперечное сечение стержня Рис. 3.4. Прямоугольное сечение

После подстановки исходных данных в формулы (3.7), (3.8) получим:

Рассмотрим неравнобокий уголок.

Для неравнобокого уголка геометрические характеристики выбираются из сортамента [3].

Для уголка (рис. 3.5,a)

аб

Рис. 3.5. Неравнобокий уголок

В рассматриваемом случае в составном сечении неравнобокий уголок развернут на 90° по отношению к его положению в сортаменте, поэтому необходимо в соответствии с его положением изменить обозначения (рис. 3.5,б):

Вычислим моменты инерции составного сечения [2, подразд. 3.1]:

; (3.9)

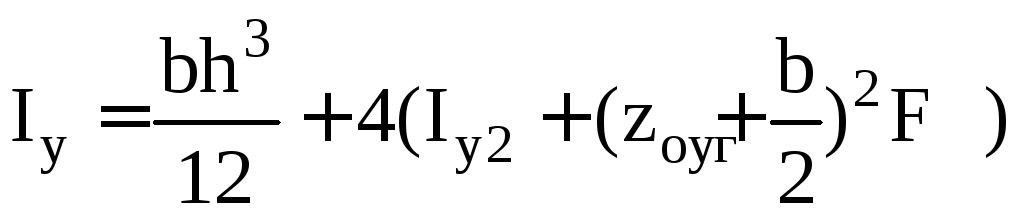. (3.10)

После подстановки исходных данных в уравнения (3.9), (3.10) получим:

Учитывая, что вычислим минимальный радиус инерции и гибкость стержня (3.1):

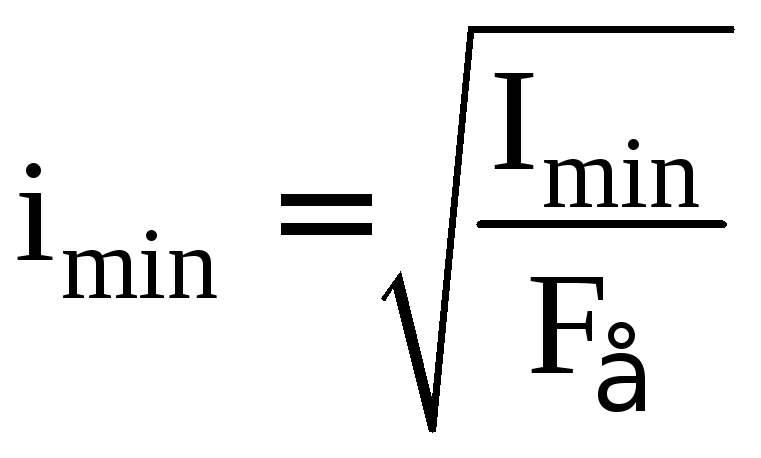; (3.11). (3.12)

После подстановки исходных данных в формулы (3.11), (3.12) получим:

Из справочной таблицы выписываем: при λ = 120 φ = 0,45; при λ = 130 φ = 0,40.

Для того чтобы найти значение φ для λ = 128,2, интерполируем внутри отрезка изменения гибкости от 130 до 120 единиц: 130 – 120 = 10; 0,45 – 0,4 = = 0,05, тогда на единицу гибкости приходится 0,005 единиц φ, а на 8,2 единиц гибкости поправка составит 0,041.

С учетом поправки для λ = 128,2 φ = 0,45 – 0,041 = 0,409.

Допускаемую нагрузку определяем исходя из условия устойчивости (3.6):

Поскольку λ = 128,2 > 100, критическая нагрузка рассчитывается по формуле Эйлера (3.2):

Коэффициент запаса устойчивости определим из выражения (3.5):

(3.13)

После подстановки исходных данных в формулу (3.13) получим: