
2473
.pdf
распределительной таблице соответствует разность потенциалов vj ui, равная тарифу этой клетки, т. е.
vj ui=cij (для xij |
). |
|
|
|
|
|
|
|
|
|
Таблица 14 |
|
|
|
|
|
|
|
|
v1 |
v2 |
v3 |
v4 |
u1 |
|
8010 |
3 |
506 |
8 |
u2 |
|
7 |
801 |
102 |
5 |
u3 |
|
304 |
8 |
4 |
701 |
Для занятых клеток составляем систему равенств:
Полагая один из потенциалов равным нулю, например 

 = 0, получим:
= 0, получим:
.
2)После нахождения потенциалов для каждой свободной клетки (xij 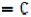 ) находим оценки
) находим оценки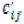 = cij
= cij .
.
3)Если все 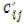
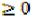 (неотрицательные), то проверяемое опорное решение является оптимальным. Если хотя бы одна оценка
(неотрицательные), то проверяемое опорное решение является оптимальным. Если хотя бы одна оценка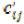
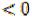 , то найденный план перевозок
, то найденный план перевозок
неоптимален, но его можно улучшить за счет загрузки этой свободной клетки и остальных занятых клеток, создав с ними цикл, перераспределив объемы перевозимых грузов. Если таких клеток несколько, загружают клетку с минимальным значением 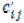 среди остальных.
среди остальных.
Для свободных клеток (табл. 11) получим:
Оценка 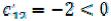 , следовательно допустимый план перевозок Х2, полученный методом минимальной стоимости (минимального тарифа) табл. 14, не является оптимальным.
, следовательно допустимый план перевозок Х2, полученный методом минимальной стоимости (минимального тарифа) табл. 14, не является оптимальным.
21

Для клетки (12) строим цикл с загруженными клетками (13), (22) и (23). Вершинам этого цикла условно приписываем знаки: свободной клетке +, следующей по часовой или против часовой занятой клетке – (минус), следующей снова +, затем –. Из поставок в клетках с отрицательными вершинами выбираем наименьшее количество груза 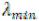 , которое прибавляем к поставкам с положительными вершинами и вычитаем из поставок в клетках с отрицательными вершинами. Баланс цикла при этом не нарушается (см. приведенную схему).
, которое прибавляем к поставкам с положительными вершинами и вычитаем из поставок в клетках с отрицательными вершинами. Баланс цикла при этом не нарушается (см. приведенную схему).
|
(12) |
|
|
(13) |
|
(12) |
(13) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
- |
50 |
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ min |
|
|
|
|
|
|
|
- |
80 |
|
|
+ |
10 |
|
30 |
|
|
60 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(22) |
(23) |
(22) |
(23) |
λmin = min{50;80}= 50
Свободной незагруженной клеткой становится клетка (13). Полученный новый план Х3 вновь проверяем на оптимальность (табл. 15).
|
|
|
|
Таблица 15 |
|
|
|
|
|
|
|
|
v1 |
v2 |
v3 |
v4 |
|
u1 |
8010 |
3 |
6 |
8 |
|
u2 |
7 |
301 |
602 |
5 |
|
u3 |
304 |
8 |
4 |
701 |
|
Для занятых клеток имеем:
.
Примем 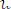

 =0, тогда получим следующие значения потенциалов:
=0, тогда получим следующие значения потенциалов:
Для свободных клеток таблицы находим оценки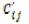
22

Полученный план перевозок Х3 вновь оказался неоптимальным, т. к. оценка клетки (21) оказалась отрицательной.
По этому плану Z(X3)=10·80+3·50+1·30+2·60+4·30+1·70=1290 у.ед.
Загружаем эту клетку, создав цикл с занятыми клетками (11), (12) и (22). Клетка
(22) становится свободной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(11) |
|
|
|
(12) |
|
|
(11) |
|
|
|
(12) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
50 |
|
|
50 |
|
|
|
|
80 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
- |
30 |
|
|
30 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(21) |
|
|
|
(22) |
|
|
(21) |
|
|
|
(22) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 16 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
|
|
|
v2 |
|
|
|
v3 |
|
v4 |
|||||
|
|
u1 |
5010 |
|
3 |
|
6 |
|
|
8 |
|
||||||||||
|
|
u2 |
7 |
|
|
1 |
|
602 |
|
|
5 |
|
|||||||||
|
|
u3 |
304 |
|
|
8 |
|
4 |
|
|
701 |
|
|||||||||
Проверяем полученный план Х4 на оптимальность. Для занятых клеток (табл. 16) получим:
Полагая получим:
получим:
При найденных значениях потенциалов все оценки свободных клеток оказываются положительными, в чем нетрудно убедиться, т.е. по затратам на перевозки полученный план является оптимальным.
Матрица перевозок этого плана имеет вид:
23

Х4=
Выводы: Путём улучшения опорного плана, полученного методом минимальной стоимости, найден оптимальный план Х4 , стоимость затрат на перевозки при котором является наименьшей и составит Z(X4)=10·50+3·80+7·30+2·60+4·30+1·70=1260 у.ед.
Контрольная работа № 8
Задание 5
Планируется деятельность двух предприятий одной отрасли в течение трёх лет. Для них выделены средства (начальные ресурсы) в размере а0 ден. ед. Средства х, вложенные в начале года в первое предприятие приносят к концу года доход f1(x) и возвращаются в размере 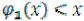 ; аналогично, средства х, вложенные во второе предприятие, дают доход f2(x) и возвращаются в размере
; аналогично, средства х, вложенные во второе предприятие, дают доход f2(x) и возвращаются в размере 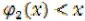 . По истечении года все возвращенные средства заново перераспределяются между предприятиями. Новых средств не поступает, доход в производство не вкладывается, а накапливается отдельно.
. По истечении года все возвращенные средства заново перераспределяются между предприятиями. Новых средств не поступает, доход в производство не вкладывается, а накапливается отдельно.
Требуется найти оптимальный способ распределения выделяемых средств между предприятиями, при котором суммарный доход обоих предприятий за три года будет максимальным. Значения параметров по каждому из вариантов приведены в табл. 17.
|
|
|
|
|
Таблица 17 |
|
|
|
|
|
|
Варианты |
Начальные |
Доходы к концу года |
Возврат средств в конце года |
||
|
средства а0 |
f1 (x) |
f2 (x) |
ϕ1 (x) |
ϕ 2 (x) |
|
(ед.) |
|
|
|
|
|
|
|
|
0,3x |
|
5.1 |
800 |
2x |
4x |
0,2x |
|
|
|
|
|
0,4x |
|
5.2 |
1000 |
3x |
2x |
0,3x |
|
|
|
|
|
0,2x |
|
5.3 |
1200 |
4x |
3x |
0,3x |
|
|
|
|
|
0,1x |
|
5.4 |
1300 |
3x |
2x |
0,2x |
|
|
|
|
|
0,2x |
|
5.5 |
900 |
2x |
3x |
0,3x |
|
|
|
|
|
0,3x |
|
5.6 |
1050 |
2x |
1,5x |
0,4x |
|
|
|
|
|
0,2x |
|
5.7 |
1400 |
x |
2x |
0,3x |
|
|
|
|
|
0,5x |
|
5.8 |
1500 |
2x |
3x |
0,6x |
|
|
|
|
|
0,2x |
|
5.9 |
900 |
2x |
3x |
0,1x |
|
|
|
|
|
0,1x |
|
5.10 |
1500 |
4x |
3x |
0,2x |
|
|
|
|
|
0,2x |
|
5.11 |
700 |
3x |
2x |
0,4x |
|
|
|
|
|
0,4x |
|
5.12 |
850 |
2x |
3x |
0,3x |
|
|
|
|
|
0,3x |
|
5.13 |
1600 |
x |
2x |
0,2x |
|
|
|
|
|
0,4x |
|
5.14 |
1100 |
2x |
4x |
0,2x |
|
|
|
|
|
0,1x |
|
5.15 |
1200 |
5x |
2x |
0,5x |
|
24
5.16 |
1300 |
x |
3x |
0,4x |
0,1x |
5.17 |
1400 |
3x |
2x |
0,3x |
0,4x |
|
|
|
|
0,4x |
|
5.18 |
1500 |
2x |
3x |
0,2x |
|
|
|
|
|
0,1x |
|
5.19 |
1700 |
5x |
x |
0,5x |
|
|
|
|
|
0,3x |
|
5.20 |
1800 |
3x |
x |
0,7x |
|
|
|
|
|
0,4x |
|
5.21 |
1900 |
2x |
3x |
0,2x |
|
|
|
|
|
0,3x |
|
5.22 |
2000 |
3x |
x |
0,5x |
|
|
|
|
|
0,5x |
|
5.23 |
2100 |
2x |
4x |
0,2x |
|
|
|
|
|
0,2x |
|
5.24 |
2000 |
4x |
2x |
0,5x |
|
|
|
|
|
0,1x |
|
5.25 |
1300 |
3x |
2x |
0,2x |
|
|
|
|
|
0,3x |
|
5.26 |
1200 |
2x |
3x |
0,1x |
|
|
|
|
|
0,3x |
|
5.27 |
1100 |
4x |
5x |
0,2x |
|
|
|
|
|
0,2x |
|
5.28 |
1000 |
2x |
3x |
0,1x |
|
|
|
|
|
0,3x |
|
5.29 |
900 |
2x |
3x |
0,2x |
|
|
|
|
|
0,1x |
|
5.30 |
1400 |
3x |
2x |
0,2x |
Задание 6
Определить оптимальные стратегии и цену игры, заданную платёжной матрицей.
6.1. |
6.2. |
6.3. |
6.4. |
6.5. |
6.6. |
6.7. |
6.8. |
6.9. |
|
6.10. |
|
|
231 |
|
32 7 |
||
|
|
|
6.11 |
|
6.12 |
|
|||
|
|
|
|
|
452 |
|
81 5 |
||
|
1 34 |
|
1 7 2 |
|
2 43 |
|
1 25 |
||
6.13 |
|
6.14 |
6 5 3 |
|
6.15 |
1 7 5 |
|
6.16 |
|
|
29 5 |
|
|
|
|
|
97 9 |
||
|
21 4 |
|
634 |
|
3 21 |
2 7 3 |
|||
6.17 |
|
6.18 |
219 |
|
6.19 |
4 7 9 |
|
6.20 |
|
|
35 2 |
|
|
|
|
9 5 4 |
|||
|
5 2 3 |
|
6 45 |
|
539 |
|
657 |
||
6.21 |
|
6.22 |
3 28 |
|
6.23 |
|
6.24 |
|
|
|
41 6 |
|
|
|
917 |
|
432 |
||
|
5 48 |
|
6 78 |
|
5 7 1 |
|
6 9 1 |
||
6.25 |
|
6.26 |
5 41 |
|
6.27 |
6 8 2 |
|
6.28 |
|
|
323 |
|
|
|
|
|
8 4 2 |
||
|
59 4 |
|
6 1 3 |
|
|
|
|
|
|
6.29 |
|
6.30 |
9 2 7 |
|
|
|
|
|
|
|
861 |
|
|
|
|
|
|
|
|
25
Задание 7
Акционерное общество распространяет акции своего предприятия, снабжая покупателей информаций о их реальной стоимости с целью получения максимальной прибыли. Покупатели акций, в соответствии с рыночной конъюнктурой, применяют свои стратегии покупки.
Определить оптимальные стратегии продавца и покупателей и цену игры, заданную платёжными матрицами (см табл. 18).
Таблица 18
Вариант |
a |
a |
a |
a |
21 |
a |
22 |
a |
23 |
Вариант |
a |
a |
a |
a |
21 |
a |
22 |
a |
23 |
|
11 |
12 |
13 |
|
|
|
|
11 |
12 |
13 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.1 |
0,3 |
0,6 |
0,3 |
0,5 |
0,4 |
0,6 |
7.16 |
0,1 |
0,5 |
0,6 |
0,4 |
0,3 |
0,7 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.2 |
0,5 |
0,6 |
0,4 |
0,3 |
0,2 |
0,6 |
7.17 |
0,2 |
0,5 |
0,3 |
0,6 |
0,1 |
0,8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.3 |
0,5 |
0,3 |
0,3 |
0,25 |
1 |
|
0,5 |
7.18 |
0,4 |
0,1 |
0,4 |
0,2 |
0,3 |
0,9 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.4 |
0,5 |
0,5 |
0,3 |
1 |
|
0,3 |
0,5 |
7.19 |
0,6 |
0,2 |
0,3 |
0,1 |
0,5 |
0,8 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.5 |
0,5 |
0,3 |
0,25 |
0,3 |
1 |
|
0,5 |
7.20 |
0,1 |
0,6 |
0,3 |
0,5 |
0,2 |
0,4 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.6 |
0,5 |
0,9 |
1 |
0,7 |
0,3 |
0,5 |
7.21 |
0,2 |
0,8 |
0,4 |
0,7 |
0,3 |
0,1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.7 |
0,5 |
0,3 |
0,25 |
0,6 |
0,2 |
0,4 |
7.22 |
0,4 |
0,5 |
0,2 |
0,3 |
0,9 |
0,6 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.8 |
0,4 |
0,25 |
0,2 |
0,3 |
1 |
|
0,4 |
7.23 |
0,6 |
0,8 |
0,9 |
0,7 |
0,2 |
0,3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
79 |
0,4 |
0,5 |
0,6 |
0,3 |
1 |
|
0,5 |
7.24 |
0,1 |
0,8 |
0,3 |
0,7 |
0,4 |
0,6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
710 |
0,5 |
0,4 |
0,25 |
0,3 |
0,2 |
0,4 |
7.25 |
0,2 |
0,9 |
0,5 |
0,8 |
0,4 |
0,3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
711 |
0,4 |
0,9 |
0,1 |
0,6 |
0,2 |
0,5 |
7.26 |
0,4 |
0,3 |
0,5 |
0,9 |
0,7 |
0,2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
712 |
0,5 |
0,1 |
0,2 |
0,7 |
0,3 |
0,1 |
7.27 |
0,1 |
0,9 |
0,2 |
0,8 |
0,6 |
0,8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.13 |
0,1 |
0,4 |
0,5 |
0,3 |
0,8 |
0,2 |
7.28 |
0,4 |
0,6 |
0,9 |
0,5 |
0,1 |
0,4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.14 |
0,2 |
0,6 |
0,1 |
0,5 |
0,4 |
0,9 |
7.29 |
0,7 |
0,4 |
0,1 |
0,4 |
0,5 |
0,8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.15 |
0,4 |
0,2 |
0,3 |
0,1 |
0,5 |
0,7 |
7.30 |
0,8 |
0,6 |
0,3 |
0,4 |
0,7 |
0,6 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 8
Даны коэффициенты прямых затрат аij (i, j= 1, 2, 3) и объём конечного потребления Yi (i = 1, 2, 3) в трёх отраслях производства. Требуется:
1.Проверить продуктивность матрицы коэффициентов прямых затрат А;
2.Определить объём валового выпуска каждого вида продукции (ден. ед.).
26
Таблица 19
Вариант |
a11 |
a12 |
a13 |
a21 |
a22 |
a23 |
a31 |
a32 |
a33 |
y |
y2 |
y3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.1 |
0,3 |
0,4 |
0,1 |
0,2 |
0,2 |
0,1 |
0,3 |
0,2 |
0,1 |
100 |
150 |
190 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2 |
0,1 |
0,2 |
0,2 |
0,1 |
0,4 |
0,2 |
0,1 |
0,0 |
0,3 |
200 |
140 |
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3 |
0,0 |
0,4 |
0,1 |
0,4 |
0,4 |
0,1 |
0,3 |
0,0 |
0,2 |
150 |
130 |
170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4 |
0,4 |
0,2 |
0,1 |
0,2 |
0,1 |
0,1 |
0,2 |
0,0 |
0,1 |
130 |
120 |
160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5 |
0,3 |
0,1 |
0,0 |
0,1 |
0,2 |
0,2 |
0,4 |
0,0 |
0,1 |
120 |
110 |
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.6 |
0,1 |
0,1 |
0,3 |
0,0 |
0,3 |
0,3 |
0,3 |
0,3 |
0,1 |
110 |
100 |
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.7 |
0,4 |
0,0 |
0,2 |
0,2 |
0,4 |
0,4 |
0,2 |
0,2 |
0,0 |
180 |
110 |
130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.8 |
0,0 |
0,3 |
0,1 |
0,3 |
0,1 |
0,1 |
0,0 |
0,0 |
0,3 |
160 |
170 |
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.9 |
0,2 |
0,4 |
0,0 |
0,4 |
0,0 |
0,0 |
0,1 |
0,1 |
0,1 |
100 |
200 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.10 |
0,0 |
0,1 |
0,3 |
0,4 |
0,1 |
0,1 |
0,2 |
0,2 |
0,2 |
100 |
80 |
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.11 |
0,2 |
0,0 |
0,2 |
0,3 |
0,2 |
0,1 |
0,2 |
0,0 |
0,1 |
110 |
90 |
190 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.12 |
0,1 |
0,3 |
0,1 |
0,2 |
0,1 |
0,3 |
0,2 |
0,1 |
0,3 |
120 |
100 |
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.13 |
0,2 |
0,4 |
0,0 |
0,1 |
0,2 |
0,0 |
0,2 |
0,2 |
0,2 |
130 |
110 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.14 |
0,3 |
0,2 |
0,2 |
0,1 |
0,1 |
0,4 |
0,1 |
0,2 |
0,0 |
140 |
120 |
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.15 |
0,1 |
0,4 |
0,1 |
0,1 |
0,4 |
0,3 |
0,1 |
0,1 |
0,2 |
150 |
130 |
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.16 |
0,4 |
0,1 |
0,2 |
0,3 |
0,2 |
0,1 |
0,1 |
0,4 |
0,0 |
130 |
200 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.17 |
0,4 |
0,3 |
0,1 |
0,2 |
0,4 |
0,3 |
0,1 |
0,2 |
0,5 |
140 |
120 |
160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.18 |
0,1 |
0,3 |
0,3 |
0,1 |
0,1 |
0,4 |
0,2 |
0,1 |
0,2 |
170 |
160 |
130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.19 |
0,1 |
0,2 |
0,0 |
0,1 |
0,1 |
0,2 |
0,0 |
0,1 |
0,4 |
120 |
100 |
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.20 |
0,2 |
0,4 |
0,0 |
0,1 |
0,2 |
0,0 |
0,2 |
0,2 |
0,2 |
130 |
110 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.21 |
0,3 |
0,2 |
0,2 |
0,1 |
0,1 |
0,4 |
0,1 |
0,2 |
0,0 |
140 |
120 |
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.22 |
0,5 |
0,3 |
0,3 |
0,2 |
0,3 |
0,2 |
0,1 |
0,2 |
0,1 |
200 |
170 |
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.23 |
0,3 |
0,1 |
0,2 |
0,2 |
0,5 |
0,1 |
0,2 |
0,3 |
0,1 |
110 |
100 |
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.24 |
0,1 |
0,4 |
0,1 |
0,1 |
0,4 |
0,3 |
0,1 |
0,1 |
0,2 |
150 |
130 |
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
27

4.25 |
0,2 |
0,4 |
0,0 |
0,1 |
0,2 |
0,0 |
0,2 |
0,2 |
0,2 |
130 |
110 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.26 |
0,4 |
0,1 |
0,1 |
0,3 |
0,1 |
0,2 |
0,1 |
0,4 |
0,1 |
170 |
150 |
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.27 |
0,1 |
0,2 |
0,2 |
0,3 |
0,2 |
0,4 |
0,1 |
0,0 |
0,3 |
180 |
160 |
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.28 |
0,1 |
0,4 |
0,2 |
0,3 |
0,3 |
0,3 |
0,1 |
0,3 |
0,4 |
190 |
170 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.29 |
0,1 |
0,4 |
0,2 |
0,3 |
0,3 |
0,3 |
0,1 |
0,3 |
0,4 |
190 |
170 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.30 |
0,2 |
0,2 |
0,0 |
0,2 |
0,3 |
0,3 |
0,3 |
0,0 |
0,0 |
200 |
180 |
170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
РЕШЕНЕ ТИПОВОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ № 8
Задание 5. Имеются два предприятия одной отрасли. При выделении каждому из них на один год х ден. ед. средств, первое предприятие обеспечивает доход в размере 3х ед. и остаток этих средств (используемый в следующем году) в количестве 0,5х ед. Второе предприятие обеспечивает доход в размере 4х ед. и остаток средств в 0,2х ед. Обоим предприятиям на три года выделено 900 ед. средств. Как их нужно распределить между предприятиями по годам, чтобы общий доход за три года был максимальным?
Задачу решим методом динамического программирования. Операцию управления производственным процессом разобьём на этапы. На каждом из них управление выберем так, чтобы оно приводило к выигрышу как на данном этапе, так и на всех последующих до конца операции. В этом состоит принцип оптимальности, сформулированный американским математиком А. Беллманом.
Разобьём весьпериоднатриэтапапогодамибудемнумероватьихначинаяспервого. Обозначим через xk и yk количество средств выделяемых каждому предприятию на k-ом этапе, а через xk + yk = аk – общее количество средств на этом этапе. Тогда первое предприятие приносит на этом этапе 3 xk , а второе 4 yk единиц дохода. Общий доход на
k-ом этапе 3xk + 4yk .
Обозначим через fk (аk) – максимальный доход, который получает отрасль от обоих предприятий на k-ом этапе и всех последующих. Тогда функциональное уравнение, отражающее принцип оптимальности Беллмана, принимает вид:
fk (аk)=max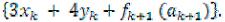
Так как xk + yk = аk , то yk = аk xk и 3xk + 4yk=3xk + 4(аk xk)= xk + 4аk . Поэтому fk (аk)=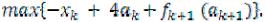

0
Кроме того, 

 – это средства выделяемые обоим предприятиям на k-ом этапе, и они определяются остатком средств, полученных на предыдущем (k–1)-ом этапе. Поэтому по условию задачи оптимальное управление на каждом этапе
– это средства выделяемые обоим предприятиям на k-ом этапе, и они определяются остатком средств, полученных на предыдущем (k–1)-ом этапе. Поэтому по условию задачи оптимальное управление на каждом этапе
28
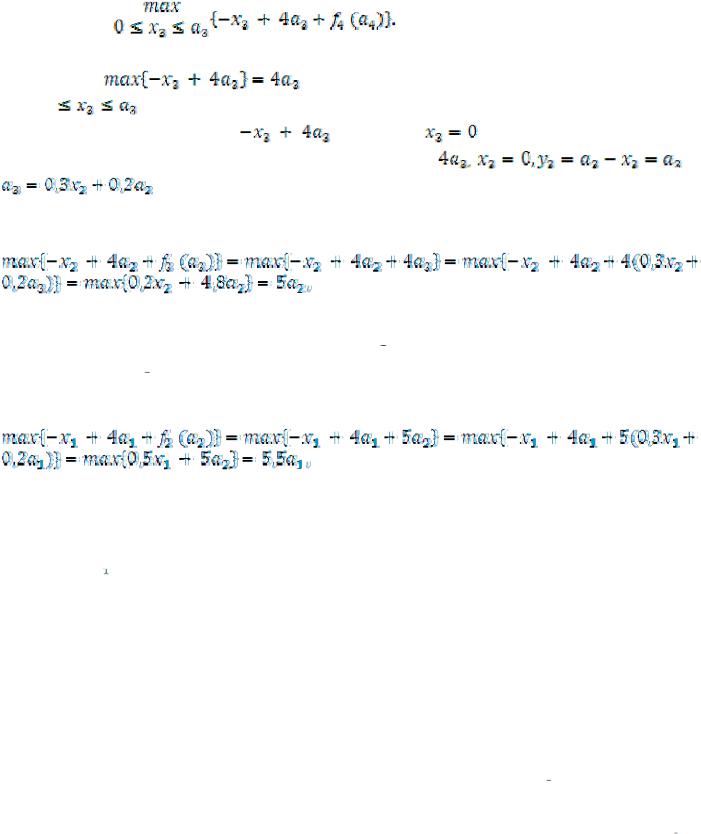
I.Условная оптимизация
Планирование начинаем с последнего третьего этапа
1.При k = 3 получаем из (2)
f3 |
(а3) = |
|
|
Так как четвёртого этапа нет, то f4(а4)=0 и |
|
||
f3 |
(а3)= |
, |
|
0 |
|
|
|
(максимум выражения ( |
) будет при |
)). |
|
Для третьего последнего этапа имеем: f3 (а3) = |
где |
||
|
, что следует из формулы (3). |
|
|
2. |
При k = 2 из (2) и (3) получаем: |
|
|
f(а2)= |
|
|
|
т.к. максимум выражения (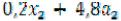 ) будет при
) будет при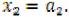
Для второго этапа имеем: f 2 (а2)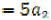 ,
, 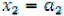 ,
, 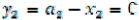 , при этом
, при этом 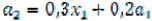 с учётом (3).
с учётом (3).
1.При k = 1 с учётом (2) и (3) получаем:
f1 (a1 ) =
при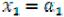 .
.
Итак, для первого этапа f 1 (а1)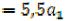 ,
, 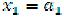 ,
, 
Процесс закончен. На первом этапе общее количество распределяемых средств известно – 
 = 900 ед. Тогда максимальный доход, получаемый обоими предприятиями за три года составит f 1 (а1)=5,5·900 = 4950 ден. ед.
= 900 ед. Тогда максимальный доход, получаемый обоими предприятиями за три года составит f 1 (а1)=5,5·900 = 4950 ден. ед.
II.Безусловная оптимизация
Выясним, каким должно быть оптимальное управление процессом выделения средств между первым и вторым предприятиями для получения максимального дохода в количестве 4950 ден. ед.
1-й год. Так как 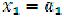 и
и 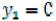 , то все средства в количестве 900 ден. ед. отдаются первому предприятию.
, то все средства в количестве 900 ден. ед. отдаются первому предприятию.
2-й год. Выделяются средства 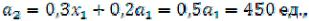
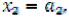
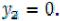 Все они передаются первому предприятию.
Все они передаются первому предприятию.
3-й год. Выделяются средства 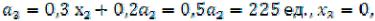
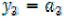 . Все они передаются второму предприятию.
. Все они передаются второму предприятию.
Результаты решения представим в виде табл. 20.
29
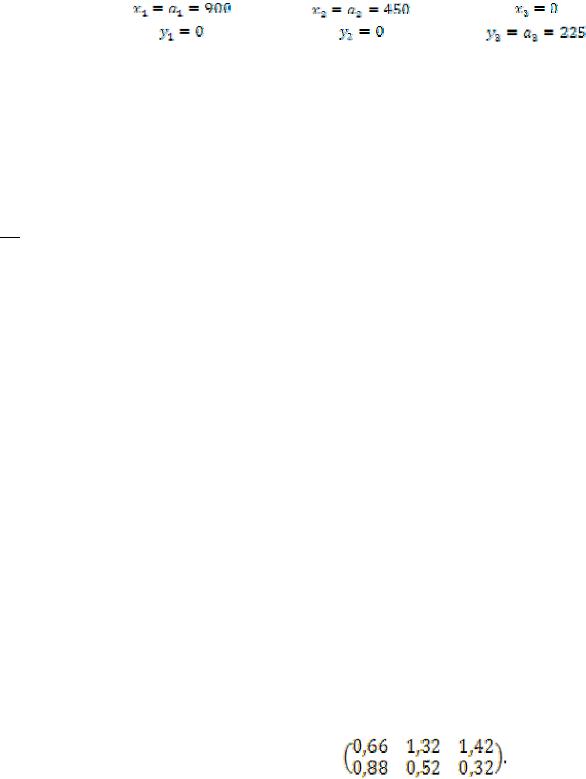
|
|
|
Таблица 20 |
|
Предприятие |
1 год |
2 год |
3 год |
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|
Начальные средства 900 |
Все начальные средства |
Все остаточные |
Все остаточные |
|
средства отдаются II- |
||||
ден. ед. |
отдаются I предпр. |
средства отдаются I-му |
||
|
|
|
му |
Задание 6. Определить оптимальные стратегии и цену игры, заданную платёжной матрицей
А=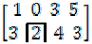 .
.
Первый игрок имеет две стратегии, определяемые строками матрицы А. Второй игрок имеет четыре стратеги, записанными в столбцах этой матрицы.
Рассмотрим стратегии первого игрока. В первой строке (стратегии) наименьший (наихудший) выигрыш равен 0, во второй строке наименьший (наихудший) выигрыш равен 2. Максимальное значение из всех наихудших выигрышей равно 2, т. е. оптимальной стратегией для первого игрока является вторая. Это значит, что как бы не играл второй игрок, первый получит гарантированно выигрыш 2, если он выберет вторую стратегию. Это так называемая нижняя цена игры, которую обозначим через α. Итак, α = 2.
Для второго игрока максимальные проигрыши равны 3, 2, 4, 5 по 1, 2, 3, 4 столбцам соответственно. Минимальный из них равен 2, что соответствует второму столбцу (второй стратегии). Это значит, что при любой стратегии первого игрока, второй игрок не проиграет больше 2, если он выберет вторую стратегию. Этот наименьший проигрыш называется верхней ценой игры и обозначается β. Итак, β = 2. Так как в нашем случае α = β = 2, то это общее значение 2 называется ценой игры и обозначается буквой υ, а соответствующий элемент а22 = 2 называется седловой точкой. Так как она есть, то соответствующие стратегии являются оптимальными, υ = 2, игра называется игрой в
чистых стратегиях и она закончена.
Выводы. Оптимальными стратегиями для первого и второго игроков являются вторые стратегии, матрица имеет седловую точку, цена игры υ = 2.
Задание 7. В качестве примера возьмём матрицу
Строки этой матрицы определяют стратегии акционерного общества (АО), столбцы – покупателей акций. Легко проверить, что седловой точки эта матрица не имеет и в чистых стратегиях задача не имеет решения. В этом случае каждый игрок будет применять свои чистые стратегии с какими – то вероятностями. Пусть это будут p1 и p2 (p1 +p2 =1) для АО и q1 , q2 , q3 (q1 + q2 + q3 = 1) для покупателей акций. Такая игра называется игрой в смешанных стратегиях.
30
