2473

градиента до тех пор, пока она не будет иметь с областью Ω единственную общую точку или не совпадет с прямой, содержащей одну из сторон многоугольника ABCDEF. В данном случае такой точкой является вершина D. Найдём координаты точки D из системы линейных уравнений как точки пересечения прямых I и II.

Максимальное значение целевой функции при этом равно:

5. Для отыскания точки, соответствующей минимальному значению целевой функции, перемещаем линию уровня Zc в направлении, противоположном направлению вектора-градиента. Наиболее удалённой точкой в этом направлении, принадлежащей области Ω, является точка А, координаты которой определяют минимальное значение Z.

Найдём координаты точки А из системы линейных уравнений как точки пересечения прямых IV и V (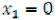): A(0; 2).

Выводы.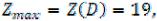

Задание 2. Симплексным методом, используя данные таблицы 6, найти план выпуска продукции по видам с учётом имеющихся ресурсов, обеспечивающий максимальный доход. Провести анализ полученного решения.

1.Составим математическую модель задачи.

Обозначим x1 и x2 – количество единиц продукции П1 и П2 , запланированных к производству (x1,2 ≥ 0).

Система ограничений по запасам сырья будет

11

Целевая функция (прибыль): Z (X ) = 3x1 + 4x2 → max .

2. Симплексный табличный метод применим только к канонической (основной) форме задачи линейного программирования, поэтому от системы ограничений – неравенств, перейдем к системе ограничений – равенств, введя дополнительные переменные x3 , x4 , x5 :

израсходованного сырья каждого вида. Перенесем все переменные в левую часть системы ограничений. В целевую функцию Z дополнительные переменные вводим с нулевыми коэффициентами.

Каноническая форма задачи принимает вид:

2x1 + 4x2 + x3 = 127x1 + 2x2 + x4 = 18 ,5x1 + 8x2 + x5 = 48

Z (X ) = 3x1 + 4x2 + 0x3 + 0x4 + 0x5 → max .

Найдем начальный опорный план (допустимое базисное решение). Система ограничений уже приведена к единичному базису, т. к. положительные дополнительные переменные входят с коэффициентом +1 каждая только в одно ограничение – равенство системы. Базисными переменными являются x3 , x4 , x5 , свободными – x1 , x2 .Пологая

Продукция не продается, ресурсы не используются, прибыль равна нулю. Необходим переход к другому опорному решению, который будем осуществлять с помощью симплексных таблиц.

3. Составим первую симплексную таблицу (табл. 7), внеся в первые три строки коэффициенты перед переменными и свободные члены системы ограничений. Элементами последней (четвертой) строки будут коэффициенты перед переменными целевой функции Z , представленной в виде равенства Z − 3x1 + 4x2 + 0x3 + 0x4 + 0x5 = 0 .

12

Z (X1 ) = 12 . Оно также не является оптимальным, так как в нижней оценочной строке есть отрицательный элемент в первом столбце. Поэтому этот столбец и будет разрешающим.

Разделим разрешающую строку на 6, а затем элементы новой второй строки умножим

Опорное (базисное) решение соответствующее этой симплексной таблице будет оптимальным, т. к. в последней оценочной строке нет отрицательных элементов. Оптимальное решение X * будет иметь вид X * = (x1*, x2 *, x3 *, x4 *, x5 *) = (2,2,0,0,22), при этом

Zmax = Z (X *) = 3 x1 * +4 x2 * +0 x3 * +0 x4 * +0 x5 * = 3 2 + 4 2 + 0 = 14 ед.

Выводы:

1.Так как в последний оценочной строке оценки свободных переменных x3 и x4 положительные, то полученное оптимальное решение единственно.

14

2.Ресурсы вида S3 будут использованны не полностью, и остаток x5 составит 22 ед.

3.Доход предприятия при реализации полученного решения составит 14 ед.

Задание 3. По исходным данным рассмотренной ранее задачи (задание 2) и ее оптимальному решению сформулировать двойственную ей задачу, используя основные теоремы двойственности. Найти оптимальное решение двойственной задачи.

1. В задании 2 сформулирована и решена задача на получение максимальной прибыли для предприятия, изготавливающего некоторую продукцию. Будем называть эту задачу исходной. Ее математическая модель имеет вид:

Z (X ) = 3x1 + 4x2 → max

2x1 + 4x2 ≤ 12

7x1 + 2x2 ≤ 18 , x1 , x2 , x3 ≥ 0

5x1 + 8x2 ≤ 48

X * = (2,2,0,0,22) , Z (X *) = 14 .

Предположим теперь, что в сложившихся экономических условиях, предприятию целесообразно продать имеющиеся запасы сырья. Возникает вопрос – по каким ценам

4 y1+2 y2 + 8y3 . В интересах предприятия, продающего сырье, стоимость сырья не должна быть меньше приносимой прибыли, т.е. должны выполняться условия:

Стоимость всего запаса сырья будет определяться функцией F (Y ) = 12y1 + 18y2 + 48y3 , где Y = Y ( y1 , y2 ) - вектор оценок. В интересах покупателя функция F(Y ) должна быть как можно меньше, т.е. F (Y ) → min .

Эта новая задача называется двойственной по отношению к исходной и ее математическая модель имеет вид:

2. Используя оптимальное решение исходной задачи, найдем оптимальное решение двойственной.

15

По первой теореме двойственности, если одна из двойственных задач имеет оптимальное решение, то и вторая также имеет оптимальное решение, причем

F (Y*) = F min = Z (X *) = Z max = 14 .

Убедимся в этом, найдя оптимальный вектор оценки ресурсов Y *.

Запишем в канонической форме математические модели обеих задач, введя для двойственной задачи дополнительные переменные y4 ≥ 0

задачи x3 , x4 , x5 соответствуют основные переменные двойственной задачи y1 , y2 , y3 . Из второй теоремы двойственности следует, что положительным компонентам

оптимального решения одной из двойственных задач соответствуют нулевые компоненты другой двойственной задачи. Учитывая это, составим соответствующую таблицу для оптимальных решений обеих задач, учитывая что X * = (2,2,0,0,22) .

Учитывая данные таблицы 10 для оптимального решения двойственной задачи, систему (2) запишем в виде:

16

Таким образом, вектор оценки ресурсов Y* = (1211 , 16 ,0,0,0) .

Оптимальное решение двойственной задачи :

F (Y*) = 12 y1 * +18 y2 + 48 y3 * = 12 1211 + 18 16 + 48 0 = 14 .

Убеждаемся, что F (Y*) = Z (X *) = 14 условных единиц.

3. Используя полученные двойственные оценки, проведем экономический анализ рассмотренной задачи.

Установим, как меняется функция оценки ресурсов F (Y ) = 12y1 * +18y2 * +48y3 * при увеличении расхода сырья на единицу. Если сырья вида S1 взять не 12, а 13=12+1, то F (Y ) = (12 + 1) y1 * +18y2 * +48y3 * = F(Y*) + y1* = F(Y*) + 1211 , т. е. оценка ресурсов увеличивается на величину двойственной оценки этого ресурса. Аналогично, увеличение на единицу

количества сырья вида S2 приведет к увеличению F (Y ) на 16 . Увеличение же на единицу

количества сырья S3 не отразиться на значении этой функции, т. к. согласно полученного решения y3 * = 0 .

По самому смыслу двойственных оценок, они определяют дефицитность сырья, т. е. чем выше двойственная оценка, тем сырье дефицитнее. В нашем примере наиболее дефицитным является сырье S1 . Сырье S2 совсем не дефицитно, т.е. избыточно, т.к. его оценка равна нулю.

Двойственные оценки позволяют определить своеобразные «нормы» взаимозаменяемости ресурсов. Так как оценки ресурсов S1 и S2 составляют 1211 и 16

соответственно, то одну единицу ресурсов S1 можно заменить 1211 : 16 = 112 = 5,5 единицами

ресурса S2 . При этом оптимальный план продукции изменится, но сумма прибыли Zmax останется на том же уровне.

Двойственные оценки тесно связаны с понятием рентабельности плана производства, в котором результат производства равен затратам, подсчитанным по двойственным оценкам. В нашем случае, производство продукции Π1 и Π 2 рентабельно, т. к. стоимость сырья на единицу продукции Π1 равна 2 1211 + 7 16 + 5 0 = 3 , а на 1 единицу

17

методических указаниях №2343.

Задание 4. Исходные данные транспортной задачи в матричной постановке представлены в табл. 11. В ней приведены станции отправления Аi (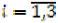) и имеющиеся на них однородные запасы груза аi, потребности в грузе bj на станциях назначения Bj, а также стоимость перевозки единицы груза cij (тариф). Необходимо спланировать матрицу перевозок Х так, чтобы общая сумма транспортных расходов Z(X) была минимальной.

Таблица 11

1. Построение допустимого плана перевозок диагональным методом

Составить план перевозок (построить опорное решение) означает найти количество груза xij , отправляемого со станции отправления Аi к потребителю на станцию назначения Bj .

Предварительно убеждаемся в том, что имеем задачу закрытого типа:

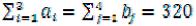– количество запасов имеющегося груза равно потребностям в нём. Следовательно, необходимое и достаточное условие совместности транспортной задачи выполняется.

1)Распределительную таблицу (табл. 12) начинаем заполнять с левой верхней

клетки (11). 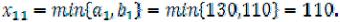Потребности В1 удовлетворены полностью, поэтому оставшиеся клетки первого столбца (21) и (31) больше не заполняются, т.е. остаются свободными. Эти клетки можно прочеркнуть (проставить в них черточки).

2)Заполняем клетку (12), т. к. у А2 имеется остаток груза в количестве 20 ед.

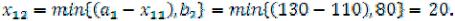запас продукта у А2 исчерпан, прочёркиваем оставшиеся клетки (13) и (14) первой строки.

3) Заполняем клетку (22). . Потребности в грузе В2 удовлетворены полностью, прочёркиваем клетку (32). Переходим к заполнению соседней клетки.

18

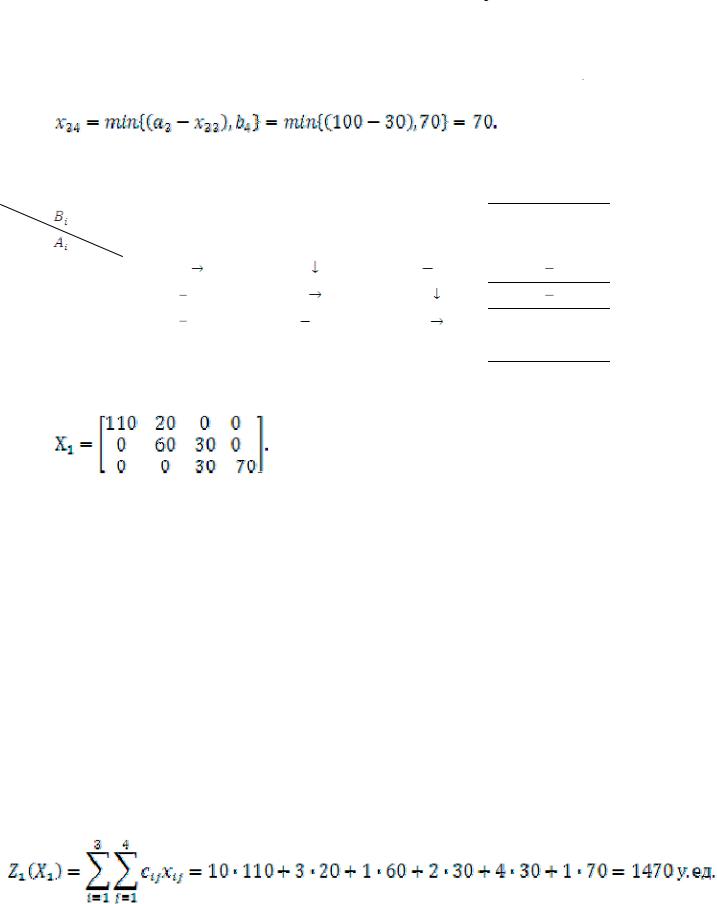
4)Клетка (23), 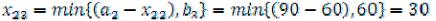Возможности отправителя А2 использованы полностью, прочёркиваем оставшуюся свободную клетку этой строки (24).

5)Клетка (33), .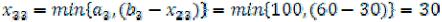

6)Последней заполняется клетка (34).

Последовательность ходов в табл. 12 показана стрелками.

Матрица перевозок (опорный план) имеет вид:

Проверим полученный опорный план перевозок (допустимое базисное решение задачи линейного программирования, каким является транспортная задача в матричной постановке) на невырожденность.

Невырожденный опорный план рассматриваемой задачи должен содержать (m + n – 1) положительных компонент xij (базисных переменных), а остальные равны нулю.

Имеем m + n – 1 = 3 + 4 – 1 = 6. Число занятых клеток (элементов, отличных от нуля, матрицы перевозок) равно 6. Следовательно, полученный план перевозок является невырожденным.

Может оказаться, что в опорном плане число занятых клеток в распределительной таблице будет меньше, чем (m+n-1). Такая задача называется вырожденной. Тогда в свободную клетку (которой обычно соответствует наименьший тариф) заносится базисный нуль и клетка считается занятой нулевой нагрузкой. Однако, занятые клетки не должны между собой образовывать циклы.

Общая стоимость по этому плану

2.Построение допустимого плана перевозок методом минимальной стоимости

Вотличие от диагонального метода здесь учитывается величина тарифов .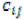

Сущность метода заключается в том, что на каждом шаге заполнять распределительную таблицу начинают с клеток, где тариф 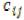наименьший. Затем остаток по столбцу или

19

строке помещается в клетку того же столбца или строки, которой соответствует следующее по величине значение 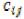и т. д. Таким образом, последовательность заполняемых клеток определяется по величине тарифа 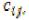а помещаемые в этих клетках величины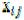определяется как в диагональном методе.

1) Заполним клетки (22) и (34), имеющие наименьший тариф, равный единице: 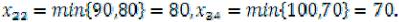Потребности в грузе потребителей В2 и В4 удовлетворены полностью, прочеркиваем оставшиеся свободные клетки второго и

четвёртого столбцов распределительной таблицы (табл. 13).

2)Клетка (23), С23=2. 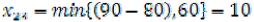. Возможности отправителя А2 исчерпаны, прочёркиваем свободные клетки второй строки.

3)Клетка (31), С31=4. 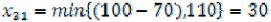. Возможности поставщика А3 исчерпаны, прочёркиваем клетку (33).

4)Заполняем клетку (13). 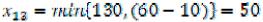. Потребности В3 полностью удовлетворены.

5) Последней заполняем клетку (11) с наибольшим тарифом С11=10.

Матрица перевозок этого опорного плана:

Полученный план перевозок является невырожденным, т. к. число занятых клеток совпадает с числом m + n – 1 = 6.

Общая стоимость перевозок

Сопоставляя полученные опорные планы перевозок видим, что общая стоимость перевозок по методу «минимальной стоимости» значительно ниже (1390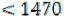), чем по диагональному методу. Проведём оценку этого плана на оптимальность и при необходимости улучшим его.

3.Проверка опорного плана на оптимальность методом потенциалов

1) Каждому поставщику Аi (i=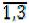) ставим в соответствие потенциал ui , а каждому получателю Вj(j=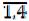) – потенциал vj (табл. 14). Каждой занятой клетке в

20