Проигрыши покупателей определяются равенствами

(*)

По теореме двойственности минимальный проигрыш покупателей равен максимальному выигрышу АО. Это значит, что стратегии покупателей должны определяться условием . Кроме того, т.к. оптимальный выигрыш АО определялся прямыми (1) и(3), т.е. при первой и третьей стратегиях покупателей, тои определить нужнои. Таким образом из (*) получаем:

.

Итак, максимальный выигрыш АО(минимальный проигрыш покупателей), равный 0,786 ед., будет тогда, когда АО свои две стратегии будет применять с вероятностями и, а покупатели свои три стратегии будут применять с вероятностями

Задание 8. Для трехотраслевой экономической системы задана матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

;

Проверить продуктивность матрицы А и определить вектор валового выпуска продукции.

Решение

1. Проверим продуктивность матрицы, вычислив обратную матрицу :

а) Находим матрицу

б) Вычисляем определитель матрицы

.

Определитель не равен нулю, матрица невырожденная и имеет обратную.

в) Транспонируем матрицу и находим присоединенную к ней матрицу , образованную алгебраическими дополнениями транспонированной матрицы.

Находим алгебраические дополнения для элементов этой матрицы:

; ;;

; ;;

; ;.

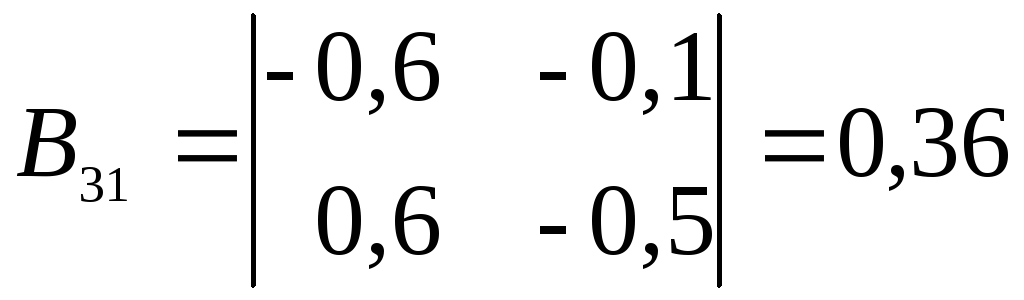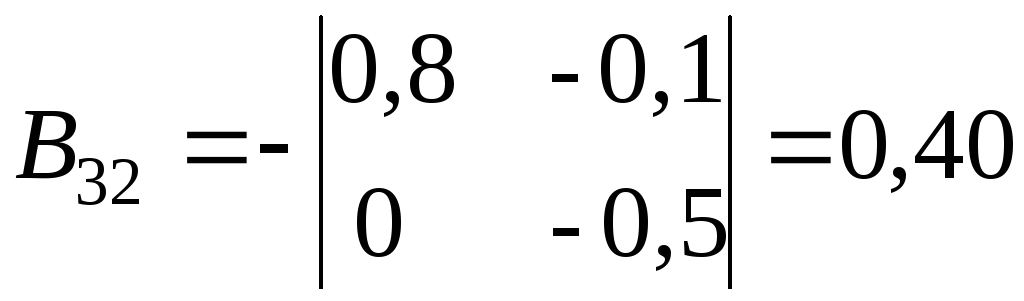Таким образом, присоединенная матрица имеет вид:

г) Находим обратную матрицу :

Сделаем проверку, чтобы убедиться в том, что при нахождении обратной матрицы не допущена ошибка в вычислениях:

Проверка проходит, найденная обратная матрица не содержит отрицательных элементов, следовательно, исходная матрица прямых затратА продуктивна.

2. Определяем вектор валового выпуска продукции:

;

Ответ: для 1, 2 и 3-й отраслей валовый выпуск составляет следующее количество единиц продукции: ;,.

40