
- •Методические указания
- •Введение
- •Работа с пакетом ms Office
- •Теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Применение числовых методов для решения задач проектирования
- •Теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Моделирование процессов системы тягового электроснабжения
- •Теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Библиографический список
Порядок выполнения работы
1. По таблице 3.1 выбрать способ решения СЛАУ.
2. Создать книгу в приложении Excel.
3. В созданной книге написать макрос, позволяющий производить расчет системы уравнений размерностью 55.
4. Оформить рабочий лист и создать на нем кнопку запуска расчета.
5. Проверить результат расчета.
Таблица 3.1
Исходные данные
|
№ п/п |
Метод решения системы уравнений |
|
0 |
Метод Гаусса |
|
1 |
Метод простых итераций с точностью е<=0.001 |
|
2 |
Метод Зейделя с точностью е<=0.001 |
|
3 |
Метод Ньютона с точностью е<=0.05 |
|
4 |
Метод Гаусса |
|
5 |
Метод прогонки |
|
6 |
Метод простых итераций с точностью е<=0.03 |
|
7 |
Метод Ньютона с точностью е<=0.002 |
|
8 |
Метод Зейделя с точностью е<=0.005 |
|
9 |
Метод прогонки |
Контрольные вопросы
1. Какие методы используются для решения СЛАУ?
2. Что такое итерация?
3. Как задается предел итераций?
4. Какой из методов наиболее удобен для решения линейных уравнений ленточного вида?
Лабораторная работа №4
«Автоматизация поиска оптимальных проектных решений»
Цель работы: на практике освоить и проверить методы выбора оптимального решения при проектировании системы тягового электроснабжения.
Теоретические сведения
Векторный показатель
эффективности работы системы
![]() позволяет
найти компромисс между требованием
удовлетворить противоречивым критериямWi,i=1,2,…,m.
Следует сразу оговориться, что найденное
таким образом решение не является
оптимальным в математическом смысле.
Это – компромисс, «одинаково неудобный
для всех».
позволяет
найти компромисс между требованием
удовлетворить противоречивым критериямWi,i=1,2,…,m.
Следует сразу оговориться, что найденное
таким образом решение не является
оптимальным в математическом смысле.
Это – компромисс, «одинаково неудобный
для всех».
1. Метод выделения главного показателя.
Производится переоценка показателей эффективности, один из них (W1) объявляется наиболее существенным, а остальные критерии (W2,W3,…,Wm) переводятся в разряд ограничений:
![]() - выбранный главный
показатель должен точно соответствовать
условию выбора.
- выбранный главный
показатель должен точно соответствовать
условию выбора.
![]() - остальные критерии
находится в допустимом интервале.
- остальные критерии
находится в допустимом интервале.
2. Свертывание показателей эффективности (линейная свертка).
Вектор показателей (Wi,W2,…,Wm) заменяется одним осредненным. Для каждого компонента вектора показателей эффективности можно найти весовой коэффициент αi , позволяющий его нормировать:
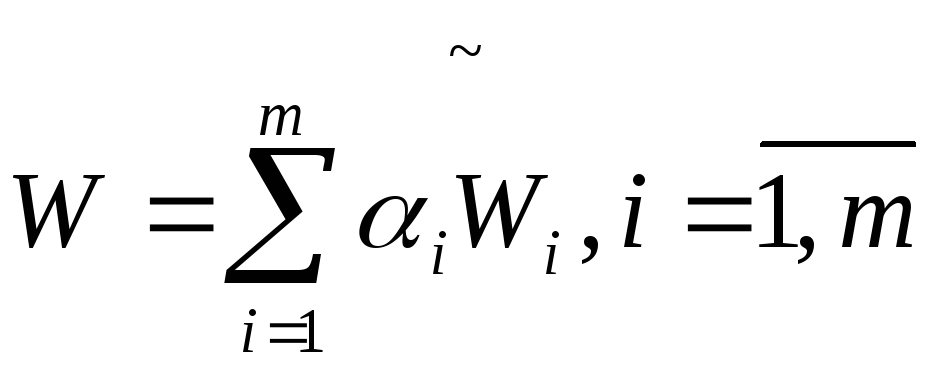 ,
,
где αi=1/(Wimax)
Таким образом, свертка будет изменяться в пределах 0≤W≤1.
Существуют и более сложные способы получения сверток: среднеквадратическое свертывание, минимаксное и т.д.
3. Последовательная оптимизация показателей с уступками.
а) сначала устанавливаются предпочтения между всеми критериями:
W1├ W2├ …├Wm;
б) ищем
![]() .
.
При
![]() заданные
экспертами оценки;
заданные
экспертами оценки;
в) ищем
![]() .
.
При
![]() заданные
экспертами оценки
заданные
экспертами оценки
W1=W1opt+ΔW1, ΔW1 -величина уступки по показателю W1;
г) ищем
![]() .
.
При
![]() заданные
экспертами оценки
заданные
экспертами оценки
Wm-1=Wm-1opt+ΔWm-1, ΔWm-1 - величина уступки по показателю Wm-1;
4. Построение множеств Парето (множеств несравнимых элементов).
Наиболее наглядно множества Парето используют для случая двух критериев (W1-W2.). Из множества различных методов, используемых для построения множеств Парето, воспользуемся методом прямоугольников:
В дальнейшем считаем, что показатели эффективности (W1,W2)→min.
а) находим в пространстве критериев W1-W2 точки со значениями координат W1min-минимальный по критерию W1 вариант построения системы, и W2min-минимальный по критерию W2 вариант построения системы;
б) проведем в указанных точках горизонтальные и вертикальные линии. Оставим для дальнейшего рассмотрения только точки, попавшие внутрь образовавшегося прямоугольника.
в) две найденные точки принадлежат множеству Парето, удаляем их из рассмотрения и повторяем процедуру построения заново.
Каждый шаг процедуры позволяет находить 2 точки множества Парето.
Замечание: то, что на каждом шаге находятся две точки множества Парето, связано с решением данной задачи на плоскости. Увеличение размерности задачи приводит к увеличению количества определяемых точек.
Окончательное решение о выборе оптимальной по многим критериям точки принимает эксперт.
