Контрольные вопросы

1. Для чего применяются таблицы Excel?

2. Как влияет количество обрабатываемых данных при автоматизации процесса расчёта токовой кривой?

3. Какие виды графиков можно построить с помощью Excel?

4. Каким образом можно произвести расчет расхода электроэнергии от движения поезда по участку?

Лабораторная работа №2

«Применение программных процедур для проведения типовых операций проектирования»

Цель работы: отработать навыки применения программирования на примере использования макросов в приложениях Microsoft Office для ускорения работы с типовыми операциями.

Теоретические сведения

Для решения типовых часто повторяющихся операций при обработке однотипных данных целесообразно использовать программные процедуры, которые позволят значительно сократить расчётное время. Операционные системы, распространенные в настоящее время, имеют удобный визуальный интерфейс, соответственно современные средства программирования позволяют создавать программы, использующие все преимущества открытого доступа к типовым процедурам по работе с информацией и созданию визуального «дружественного» интерфейса.

Программой Visual Basic реализован визуальный стиль программирования. При этом не столько программируется, сколько проектируете приложение. Первая задача при этом — создать рабочую среду, прежде чем начать набирать первую строку кода. Упрощенная версия Visual Basic встроена в пакет программ MS Office. В приложениях пакета можно составлять небольшие программы – макросы, которые позволяют автоматизировать работу с приложением.

Порядок выполнения работы

1. Открыть книгу Excel, созданную в лабораторной работе №1.

2. Написать код программы, вычисляющей средние токи правого и левого плеч расчётной ТП2:

, (1)

где n₀ - количество отрезков на кривой поездного тока (межпоездной интервал 10 минут);

- среднее значение тока поезда за рассматриваемый промежуток времени t_i;

t - время хода поезда по фидерной зоне (скорость движения принять постоянной, равной 50 км/ч).

3. Написать код программы, вычисляющей среднеквадратичные токи правого и левого плеч расчётной ТП2:

. (2)

4. Составить объединенный код программы, которая рассчитывает производит автоматическое разложение токовой кривой для ТП1 и ТП3. Данные поместить в следующие столбцы.

5. На рабочем листе создать кнопку, запускающую эту программу.

Контрольные вопросы

1. Что такое макрос?

2. Что такое объектно-ориентированное программирование?

3. Какие преимущества даёт использование процедур в программе?

Применение числовых методов для решения задач проектирования

Лабораторная работа №3

«Решение систем линейных алгебраических уравнений»

Цель работы: на практике освоить и проверить методы расчета систем линейных алгебраических уравнений.

Теоретические сведения

Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ — многими пакетами прикладных программ, позволяющих решать различные возникающие на практике линейные системы. Чтобы ориентироваться среди методов и программ и в нужный момент сделать оптимальный выбор, нужно разбираться в основах построений методов и алгоритмов, учитывающих специфику постановок задач, знать их сильные и слабые стороны и границы применимости.

Все методы решения линейных алгебраических задач (наряду с задачей решения СЛАУ, это и вычисление определителей, и обращение матриц, и задачи на собственные значения) можно разбить на два класса: прямые и итерационные. Прямые методы – это такие методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (в связи с чем к классу прямых методов применяют еще название точные методы). Итерационными методами называют методы, в которых точное решение может быть получено лишь в результате бесконечного повторения единообразных (как правило, простых) действий.

Другое ограничение будет касаться рассматриваемых систем. Условимся говорить о численном решении таких СЛАУ, у которых число уравнений совпадает с числом вещественных неизвестных, причем будем предполагать наличие единственного решения, если существование и единственность не следует из каких-либо условий.

Такое ограничение здесь довольно естественно, так как решение и недоопределенных, и переопределенных систем, а также систем с комплексными коэффициентами и переменными, в конечном счете, сводится к решению однозначно определенных вещественных систем.

Итак, изучается вопрос о численном решении систем вида

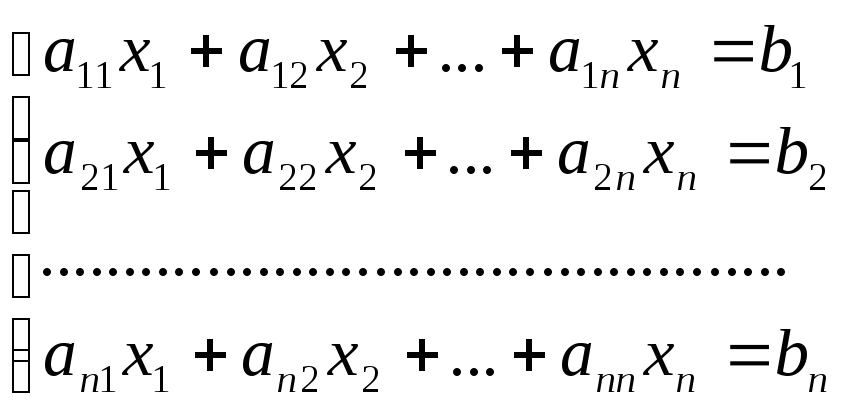(3)

или иначе, векторно-матричных уравнений

Ах = b,

где b = (b₁, b₂, …, b_n)^T — вектор свободных членов и x = (x₁, x₂,…, x_n)^Т — вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а А = — вещественнаяnn-матрица коэффициентов данной системы. Эффективность способов решения системы во многом зависит от структуры и свойств матрицы А: размера, обусловленности, симметричности, заполненности (т.е. соотношения между числом ненулевых и нулевых элементов), специфики расположения ненулевых элементов в матрице и др.