
математика Раздел1 практика
.pdf
I Элементы линейной и векторной алгебры и аналитической геометрии
Тема 1.1 Вычисление определителей 2-го, 3-го и 4-го порядков.
Определитель 2 – го порядка |
|
|
|
|||||
|
|
Произведение |
Определитель 3 – го порядка, |
|||||
|
элементов по главной |
по правилу треугольника |
||||||
|
|
диагонали |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведение элементов по побочной диагонали
Образцы решения задач:
ПРИМЕР Вычислить определитель 2-го порядка
2 3
1 4
РЕШЕНИЕ: Вычисление определителя 2-го порядка проводится по схеме, представленной в таблице 1:
a |
b |
a d b c , поэтому для нашей задачи имеем: |
|||||
c |
d |
||||||
|
|
|
|
|
|||
|
|
|
3 |
|
2 4 3 ( 1) 8 3 11. |
||
|
|
|
2 |
|
|||
|
|
|
1 |
4 |
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
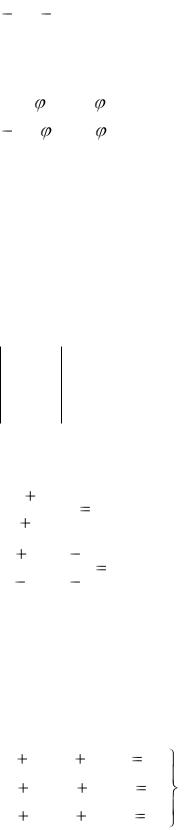
ПРИМЕР Вычислить определитель 3-го порядка, пользуясь правилом треугольника
2 3 1
0 2 1
3 1 0
РЕШЕНИЕ: Вычисление определителя 3-го порядка по правилу треугольника проводится по схеме, приведенной в таблице выше.
В нашем случае, имеем:
2 |
3 |
1 |
|
|
|
|
0 |
2 |
1 |
2 2 0 0 1 ( 1) 3 1 3 (3 2 ( 1) 1 1 2 0 3 0) |
|||
3 |
1 |
0 |
|
|
|
|
0 |
0 |
9 |
6 |
2 |
0 |
13 |
|
|
|
|
|
|
1 |
Задания для решения:
1. Вычислить определители второго порядка:
а) |
1 |
2 |
|
|
|
|
||||
|
|
3 |
4 |
|
|
|
|
|||
|
|
|
|
, |
|
|
||||
|
|
|
|
|
|
|
||||
|
|
x |
xy |
|
|
|
|
|||
б) |
|
|
|
|
|
|||||
|
|
1 |
y |
|
, |
|
|
|||
|
|
|
|
|
|
|||||
в) |
|
cos |
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
||||
|
|
sin |
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
2. Вычислить определители третьего порядка:
|
|
3 |
2 |
1 |
|
а) |
|
2 |
5 |
3 |
|
|
|
3 |
4 |
2 |
, |
|
|
2 |
3 |
|
|
|
|
1 |
|
||
б) |
|
4 |
5 |
6 |
|
|
|
7 |
8 |
9 |
, |
|
1 |
1 |
1 |
|
|
в) |
1 |
2 |
3 |
|
|
13 6 .
3.Решить уравнения, воспользовавшись правилом нахождения определителя 2-го порядка:
а) |
|
2x |
3 |
3 |
|
|
0 |
|
|
x |
5 |
2 |
|
|
, |
б) |
|
x |
3 |
x |
1 |
|
|
|
|
0 |
|||||
|
|
||||||
|
|
7 |
x |
x |
1 |
|
. |
|
|
|
|
|
|
|
Тема 1.2 Решение систем линейных уравнений по правилу Крамера и методом Гаусса.
Правило Крамера:
Пусть дана система трех линейных уравнений с тремя неизвестными:
a11x1 |
a12x2 |
a13x3 |
b1 |
|
a 21x1 |
a 22x2 |
a 23x3 |
b2 |
(1.2.1) |
a31x1 |
a32x2 |
a33x3 |
b3 |
|
2

|
a11 |
a12 |
a13 |
Обозначим через |
a 21 |
a 22 |
a 23 – главный определитель системы. |
a31 a32 a33
Если 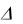 0 , то система (1.2.1) имеет единственное решение, которое находится по формулам Крамера:
0 , то система (1.2.1) имеет единственное решение, которое находится по формулам Крамера:
|
|
|
|
|
|
x |
|
|
x1 |
, x |
|
|
x 2 |
, |
x |
|
|
x 3 |
|
(1.2.2) |
||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b1 |
a12 |
a13 |
|
|
|
a11 |
b1 |
a13 |
|
|
|
|
|
a11 |
a12 |
b1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где x |
1 |
b2 |
a22 |
a23 |
; x |
2 |
|
a21 |
b2 |
a23 |
; |
|
x |
3 |
|
a 21 |
a 22 |
b2 |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b3 |
a32 |
a33 |
|
|
|
a31 |
b3 |
a33 |
|
|
|
|
|
a31 |
a32 |
b3 |
|
|||
Образцы решения задач:
ПРИМЕР. Дана система линейных уравнений:
х1 х2 х3  4,
4,
х1 2х2 4х3 4, х1 3х2 9х3 2.
Доказать совместность системы и решить ее по формулам Крамера. РЕШЕНИЕ: Совместность данной системы докажем используя теорему Крамера, а именно: если главный определитель системы отличен от нуля, то система имеет единственное решение.
1 |
1 |
1 |
|
1 |
2 |
4 |
18+ 3 + 4 -2 -12 – 9= 2 0 . |
1 |
3 |
9 |
|
|
|
|
|
Решим систему уравнений по формулам Крамера. Вычислим определители
х1 , х 2 , |
|
х 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
1 |
|
|
|
1 |
|
4 |
1 |
|
|
|
1 |
1 |
4 |
|
|
|
||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
х1 |
4 2 4 |
4 ; |
х 2 |
1 4 |
4 |
6 ; |
х 3 |
1 2 4 |
-2 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
3 |
9 |
|
|
|
1 |
|
2 |
9 |
|
|
|
1 |
3 |
2 |
|
|
|
||||
По формулам Крамера получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
х1 |
х1 |
4 |
|
2; |
х2 |
х 2 |
6 |
|
3; |
х3 |
|
х 3 |
|
|
2 |
|
|
1. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, тройка чисел 2; 3; |
1 |
является решением системы. |
|
|||||||||||||||||||||
ПРИМЕР. Дана система линейных уравнений
3

|
х1 |
х2 х3 |
1, |
|
|
|
|
|
|
|
|
|
|
||
|
8х1 |
3х2 |
6х3 |
2, |
|
|
|
|
|
|
|
|
|
|
|
|
4х1 |
х2 |
3х3 |
3. |
|
|
|
|
|
|
|
|
|
|
|
Доказать ее совместность и решить |
тремя способами методом Гаусса. |
|
|||||||||||||
РЕШЕНИЕ: Решим систему уравнений методом Гаусса. |
|
||||||||||||||
|
|
|
|
|
|
|
|
Первое уравнение системы умножим на ( 8) и сложим |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
х1 |
х2 |
|
х3 |
1, |
|
|
со вторым уравнением, результат сложения запишем |
|
|||||||
|
|
|
вторым |
уравнением в новой системе. Затем первое |
|
||||||||||
8х1 |
3х2 |
6х3 |
2, |
|
|
|
|||||||||
|
|
уравнение системы умножим на 4 и сложим с третьим |
|
||||||||||||
4х1 |
х2 |
3х3 |
3, |
|
|
||||||||||
|
уравнением системы, результат запишем третьим |
|
|||||||||||||
|
|
|
|
|
|
|
уравнением . |
|
|
|
|||||
|
х1 |
х2 |
х3 |
1, |
|
|
|
|
|
|
|
||||
|
|
|
Умножим второе уравнение системы на 3, а третье |
|
|
||||||||||
|
|
|
уравнение на ( 5) и сложим, результат запишем |
|
|
||||||||||
|
|
5х2 |
2х3 |
6, |
|
|
|
|
|||||||
|
|
|
|
третьим уравнением эквивалентно преобразованной |
|
|
|||||||||
|
3х2 |
х3 |
1, |
|
|
|
|
|
|||||||
|
|
|
|
системы. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
х1 |
х2 |
х3 |
1, |
|
|
х1 |
1 |
|
|
х2 |
х3 , |
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
5х2 |
2х3 |
6, |
|
|
х2 |
|
( 6 2х3 ) , |
|
|||||
|
|
|
|
5 |
|
|
|||||||||
|
х3 |
13, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
х3 |
13. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
х1 |
8, |
х2 |
4, |
х3 |
13. |
|
|
|
|
|
||||
Задания для решения:
1. Доказать соместность систем и решить их по правилу Крамера:
а) |
x1 |
x2 |
4, |
2x1 |
x2 |
5. |
x1 2x2 3x3 3, б) 2x1 6x2 4x3 6,
3x1 10x2 8x3 21.
2. Найти решения линейной системы уравнений, используя метод Гаусса:
x 2y 3z 5, а) 4x 5y 6z 8,
7x |
8y |
2. |
x1 2x2 3x3 0, б) 4x1 5x2 6x3 0,
7x1 8x2 9x3 0.
4
Тема 1.3 Действие над матрицами. Нахождение обратной матрицы. Решение систем линейных уравнений матричным методом.
Матрицы. Действия над матрицами.
Матрицей называется прямоугольная таблица, содержащая m n чисел, расположенных в m строк и n столбцов
a11 a12 a13 a1n |
|
|
|
|
|
|
|
|
|
||
a21 |
a22 a23 a2n |
или сокращенно A (aij ) , где i |
1, m – номер строки, |
||||||||
A |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
am1 am2 am3 am n |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
j 1, n – номер столбца. |
|
|
|
|
|||
Сложение матриц |
|
Умножение |
Умножение матриц |
||||||||
Операция |
|
сложения |
матрицы на число |
Операция |
умножения |
двух |
|||||
матриц |
|
вводится |
Чтобы |
умножить |
матриц вводится только для |
||||||
только |
для |
матриц |
матрицу |
на |
число |
случая, |
|
когда |
|
число |
|
одинакового размера |
|
необходимо каждый |
столбцов |
первой |
матрицы |
||||||
+ |
|
|
|
элемент |
матрицы |
равно |
числу строк второй |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
умножить на это матрицы. |
|
|
|||||
|
|
|
|
число |
|
|
|
|
|
|
|
Минором |
какого-либо |
элемента |
Алгебраическим дополнением |
|
|||||||
определителя |
|
|
называется |
элемента аi j называется его минор, |
|||||||
определитель, |
полученный |
из |
взятый со знаком (–1)i + j |
|
|
||||||
данного вычеркиванием той строки и |
|
Aij |
( |
1)i j M ij |
|
|
|||||
того столбца, которым принадлежит |
Определитель |
|
равен |
|
сумме |
||||||
данный элемент |
|
|
|
|
|
||||||
|
|
|
произведений |
элементов |
любой |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
строки |
(столбца) |
на |
их |
||
|
|
|
|
|
|
алгебраические дополнения. |
|
||||
|
|
Минор элемента определител |
|
|
|
|
|
|
|||
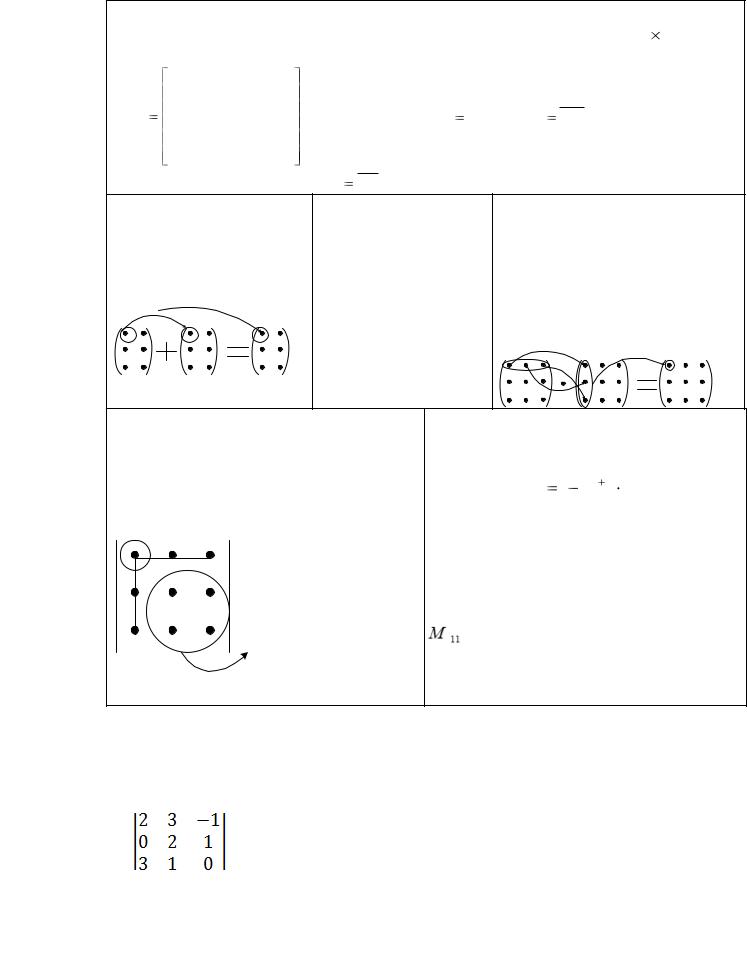
Образцы решения задач:
ПРИМЕР. Вычислить определитель 3-го порядка методом разложения по элементам второй строки
.
5

РЕШЕНИЕ: Вычисление определителя 3-го порядка методом разложения по элементам второй строки проводится по следующей формуле:
|
a11 |
a12 |
a13 |
|
|
|
a21 |
a22 |
a23 |
a21 A21 a22 |
A22 a23 A23 , |
|
a31 |
a32 |
a33 |
|
|
где |
Aij — |
алгебраические |
дополнения элементов aij в данном |
||
определителе:
A |
( 1)i j M |
ij |
, а |
M |
ij |
— миноры, соответствующие элементам |
a |
ij |
ij |
|
|
|
|
|
определителя, которые являются определителями второго порядка, получаемые из данного определителя путем вычеркивания строки i и столбца j.
Следовательно, мы имеем:
ПРИМЕР. Найти произведение двух матриц A и B, если
.
РЕШЕНИЕ: Операция умножения двух матриц вводится только для случая,
когда число столбцов первой матрицы равно числу строк второй матрицы.
Рассмотрим на примере:
В нашем случае имеем:
6

ПРИМЕР. Найти матрицу  , обратную для матрицы A, где
, обратную для матрицы A, где
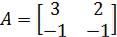 .
.
РЕШЕНИЕ: Обратная матрица находится по следующей формуле:
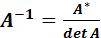 , где
, где  союзная матрица к матрице
союзная матрица к матрице  , а
, а
определитель, составленный из элементов данной матрицы. Подставляя, получаем: 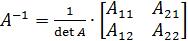 . В нашем случае:
. В нашем случае:
1. Находим определитель данной матрицы:
 , следовательно
, следовательно
обратная матрица существует.
2. Находим союзную матрицу к матрице  , т.е.
, т.е. 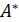 . Для этого найдем алгебраические дополнения элементов
. Для этого найдем алгебраические дополнения элементов 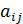 в данной матрице.
в данной матрице.
; |
; |
; |
. |
Получаем:
Подставляем полученные результаты в формулу и находим обратную матрицу  :
:  .
.
Решим систему линейных уравнений матричным методом. Обозначим:
|
|
|
|
|
1 |
1 |
1 |
|
|
|
х1 |
|
|
4 |
|
|
|
|
А = 1 2 4 |
; |
|
Х = х2 ; |
В = 4 . |
|
|||||||
|
|
|
|
|
1 |
3 |
9 |
|
|
|
х3 |
|
|
2 |
|
Тогда данную систему можно записать в виде: |
АХ |
В ,откуда |
Х А 1В , |
||||||||||||
где |
А 1– |
обратная матрица. Найдем |
А 1, |
зная, что |
|
||||||||||
|
|
|
|
|
A11 |
A21 |
|
A31 |
|
|
|
|
|
|
|
А 1 |
= |
|
1 |
|
A |
A |
|
A |
, |
где |
А |
- |
алгебраические |
дополнения |
|
|
|
|
|
||||||||||||
det A |
|
||||||||||||||
|
|
12 |
22 |
|
32 |
|
|
ij |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
A13 |
A23 |
|
A33 |
|
|
|
|
|
|
|
элементов аij матрицы А. |
|
|
|
|
|
|
|
|
|||||||
Аij |
( 1)i |
|
j Mij , |
где |
M ij - миноры элементов аij |
матрицы А. |
|||||||||
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|

|
1 |
1 |
1 |
|
det A = |
1 |
2 |
4 |
= 2 . |
|
1 |
3 |
9 |
|
|
|
|
|
|
Так как det A |
|
|
0 , то существует обратная матрица. |
|
|
|
|
|
|
|||||||||||||||||
А11 = |
(-1)1+1 |
|
|
|
4 |
|
18 |
2 |
6 ; |
|
А12 = |
|
-5 ; |
А13 |
= |
1 ; |
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|||||||||||||||||||
|
3 |
9 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
А21 |
= |
(-1)2+1 |
|
|
|
1 |
|
|
(9 |
3) |
6 ; |
А22 |
= |
8; |
А23 |
= |
-2 ; |
|
|
|
||||||
|
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
3 |
9 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
А31 |
= |
(-1)3+1 |
|
|
1 |
|
|
|
4 |
2 |
2 |
|
А32 |
= |
-3; |
А33 |
= |
1 ; |
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
4 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
6 |
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
А-1 = |
1 |
5 |
8 |
3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
6 |
6 |
2 |
|
4 |
|
1 |
|
|
24 |
24 |
4 |
|
1 |
4 |
||||||
Х А 1В = |
|
5 8 |
3 |
|
4 |
= |
|
|
20 32 |
6 |
= |
6 = |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
1 |
2 |
1 |
|
2 |
2 |
|
|
4 |
8 |
2 |
|
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом , |
х1 = 2; |
х2 = 3; |
х3 = -1. |
|
|
|
|
|
|
|
|
|||||||||||||||
Проверим правильность |
вычисления |
обратной |
матрицы, |
используя |
||||||||||||||||||||||
матричное умножение, т.е. А А-1 = А-1 А = Е .
|
1 |
|
1 |
1 |
|
|
|
|
6 |
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
4 |
|
1 |
|
5 |
8 |
|
3 |
= |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
3 |
9 |
|
|
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
6 |
5 |
|
1 |
|
|
|
6 |
8 |
2 |
|
2 |
3 |
1 |
|
|
2 |
0 |
0 |
|
= |
1 |
|
6 |
10 4 |
|
|
|
6 16 8 |
2 6 4 |
= |
1 |
0 |
2 0 |
= |
||||||||
2 |
|
|
|
|
2 |
|||||||||||||||||
|
|
6 |
15 |
9 |
2 |
6 |
24 |
|
18 |
2 |
9 |
9 |
|
0 |
0 |
2 |
||||||
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
1 |
0 |
|
= Е . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично доказывается, |
|
что |
А-1 А = Е. Значит А-1, |
найдена верно. |
||||||||||||||||||
|
|
Ответ: |
2; |
3; |
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задания для решения:
8
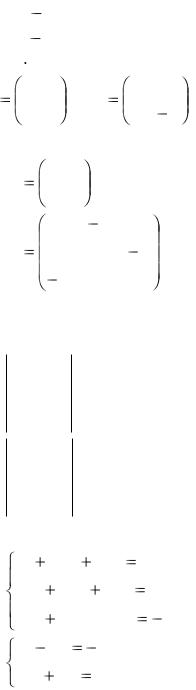
1. Найти линенйные комбинации матриц:
а) 3A 2B , б) 2B 5A ,
в)
A |
1 |
2 |
, B |
0 |
1 . |
|
3 |
4 |
|
1 |
2 |
2. Для матрицы А, найти ей обратную:
а) A |
1 |
2 |
, |
|
|
3 |
4 |
|
|
|
1 |
|
2 |
0 |
б) A |
3 |
|
5 |
7 . |
4 1 2
3. Вычислить определить 3-го порядка разложением по какойнибудь строке или столбцу:
2 0 3 а) 7 1 6 ,
6 0 5
0 a 0 б) b c d .
0 c 0
4. Решить системы уравнений матричным методом:
|
x1 |
2x2 |
3x3 |
6, |
а) |
4x1 |
5x2 |
6x3 |
9, |
|
7x1 |
8x2 |
|
6. |
б) |
x1 |
x2 |
1, |
|
2x1 |
x2 |
7. |
|
9
|
|
|
Тема 1.4 Векторы. Линейные операции над векторами. Координаты |
||||||||||||||||||||||||||||
вектора. Линейные операции над векторами в координатной форме. |
|||||||||||||||||||||||||||||||
Скалярное произведение векторов, и его приложения. |
|
|
|
|
|
|
|||||||||||||||||||||||||
Векторы. Линейные операции над векторами. Скалярное произведение |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторов. |
|
|
|
|
|
|
|
|
|
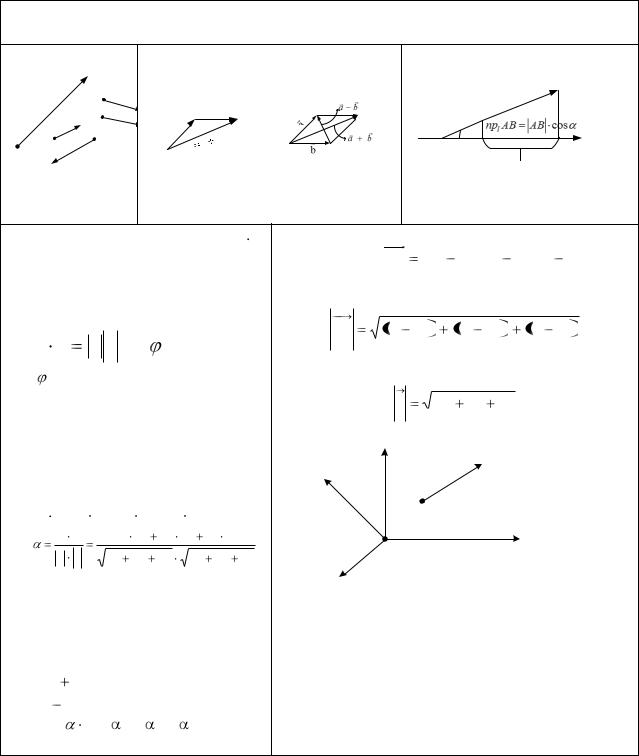
Вектор - это |
|
|
|
Сложение векторов |
|
|
Проекция вектора на ось |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
правило |
|
|
правило |
|
|
|
|
|
|
|
В |
|
||
|
|
|
|
|
|
ный |
|
|
|
|
|
треугольника |
параллелограмма |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
е |
|
ок |
|
|
|
|
|
Ра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
вл |
|
|
|
|
|
|
|
вные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
а |
трез |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
А |
|
|
|
|
|
|||||
|
пр |
|
|
|
|
|
|
векто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
На |
о |
|
|
|
|
|
|
|
|
|
|
ра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ы |
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
не |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
А |
|
|
л |
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
л |
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
||||
|
Ко |
|
|
ек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
||||||||
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекция вектора |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на ось |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координаты |
|
|
|
|
|||
Скалярным |
произведением |
a |
b |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
двух |
|
ненулевых |
векторов |
a |
и |
вектора AB |
(x 2 |
x1; y2 |
|
y1; z2 |
z1 ) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b называется |
|
|
число, |
|
равное |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
произведению длин этих векторов на |
|
Длина вектора |
|
|
|
||||||||||||||||||||||||||
косинус угла между ними |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
x2 |
x1 |
2 |
y2 |
y1 |
2 |
z2 |
z1 |
2 |
|||
|
a |
|
b |
|
|
|
|
|
a b cos |
, |
(1.4.1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где |
|
– угол между векторами |
|
и |
|
|
|
или |
|
|
|
|
|
||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 2 |
Y 2 |
Z 2 |
|
|
||
b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|||||
Скалярное |
|
произведение |
|
двух |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
векторов |
|
|
|
в |
координатной |
форме |
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||
равно |
|
|
|
|
|
|
|
|
|
|
|
сумме |
|
произведений |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(x2; y2; z2) |
||||||||||||||
соответствующих |
координат |
этих |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
векторов, т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
A(x1; y1; z1) |
|
|
|
|
||||
|
a |
|
b =x1 x2+ y1 |
y2+ z1 |
z2, тогда |
; |
|
|
|
|
|
||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x1 |
x 2 |
y1 y2 z1 z 2 |
|
z |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
a b |
|
|
|
) |
|
|
|
|
|
|
y |
|
|
||||||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x 2 y2 |
z 2 |
x 2 |
y2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a b |
|
z |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Линейные операции над векторами |
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
в координатной форме |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пусть в системе координат Оху даны |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
векторы a =(x1 ; y1 |
; z1), b =(x2; y2 ; z2) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a b = (x1+ x2; y1 + y2; z1 + z2). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
a b = (x1–x2; y1 –y2; z1 – z2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a = ( х1; у1; z1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
