Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет природообустройства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

математика Раздел1 практика

.pdf

Скачиваний:

Добавлен:

09.04.2015

Размер:

3.54 Mб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Образцы решения задач:

, образующий с осью Оu угол 1 = 1200, и вектор

ПРИМЕР. Дан вектор a

образующий с той же осью угол

2 = 600. Найти проекцию суммы

+ b +

где c

= 2 b , на ось Оu, если известно, что a

= 8, b = 6.

РЕШЕНИЕ:

1 = 8 cos 1200 = 8

прOu a =

cos

(

) = –4;

2 = 6 cos 600 = 6

прOu b =

cos

= 3.

прOu c

= прOu(2 b ) = 2 прOu b = 2 3 = 6. Значит,

прOu ( a

+ b

+ c ) = прOu a

+ прOu b + прOu c = –4 + 3 + 6 = 5.

b ,

c ,

ПРИМЕР. В некотором базисе даны векторы

(–2, 1, 3) и b (3, –1, 2).

Вычислить координаты векторов c = 2 a

+ 3 b и d

= 3 a – 4 b .

РЕШЕНИЕ:

Вычислим координаты векторов 2 a , 3 b , 3 a , и 4 b

2 a = (2 (–2), 2 1, 2 3) = (–4, 2, 6);

3 b = (3 3, 3 (–1), 3 2) = (9, –3, 6);

3 a = (3 (–2), 3 1, 3 3) = (–6, 3, 9);

4 b = (4 3, 4(–1), 4 2) = (12, –4, 8).

Вычислим теперь координаты c

и d

c= (–4 + 9, 2 + (–3), 6 + 6) = (5, –1, 12) ;

d= (–6 – 12, 3 – (–4), 9 – 8) = (–18, 7, 1).

ПРИМЕР. Найти координаты начала вектора a (1; 3; –7), если его конец

совпадает с точкой B(2, –5, 1).

РЕШЕНИЕ: Пусть начало вектора a есть точка A(x1, y1, z1). По формуле (2) получаем (1; 3; –7) = (2 –x1, –5 – y1, 1 – z1). Откуда находим координаты

точки A: 2 –x1 = 1, –5 – y1 = 3, 1 – z1 = –7, т.е. x1 = 1, y1 = –8, z1 = 8.

Итак, начало вектора есть точка A(1, –8, 8).

ПРИМЕР.

Пусть a = 5 i	+ 3 j – 2 k , b = 4 i +	j + 7 k . Вычислить a • b .

РЕШЕНИЕ:

a • b = 5 4+3 1+(–2) 7=20+3–14=9.

Из определения скалярного произведения следует, что

x1 x2

y1 y2

z1 z2

a b

cos =

Эта формула позволяет вычислить угол между двумя векторами, заданными своими координатами.

ПРИМЕР. Вычислить угол между векторами a
ПРИМЕР. Вычислить угол между векторами a										= (2; - 3; 0) и b = (4; 2; -1) .
РЕШЕНИЕ: Находим вначале

	a • b = 2 4			3 2 0 ( 1) 8 6 0 2.
Вычислим теперь

	a	22	( 3)2			02	4 9	13 и

	b	42	22	( 1)2			16 4 1	21 .
Тогда cos( a ,							2	2			2
					b )=		2	2	,	arccos	2	.


						13	21	273			273

Кроме широкого применения скалярного произведения в самой математике оно используется в физике, например, для вычисления работы. Известно, что работа А вычисляется по формуле

A F

s , где F -вектор силы, s -вектор пути.

ПРИМЕР Даны три силы: F1

(2; 5;1) ,

F2 (1;2; 6) ,

F3 ( 4; 3;3) ,

приложенные

в одной точке.

Вычислить

работу,

произведенную

равнодействующей силой по перемещению материальной точки
прямолинейно от точки М (4; 2; -8) до точки N (3; -2; -5).

РЕШЕНИЕ: Обозначим равнодействующую заданных трех сил символом F

и найдем координаты этого вектора из равенства F								F1		F2	F3	. Получаем

F 2 1 4; 5 2	3;1		6	3 или F	1;	6;	2 .
									1;	4;3) .

Путь s = MN . Аналогично, как и для F							имеем s (
			1	1	6	4	2	3	1	24	6	19 (ед.
Тогда A= F		s	1	1	6	4	2	3	1	24	6	19 (ед.

работы).

Скалярное произведение можно использовать и в экономике.

ПРИМЕР. Бизнесмен имеет в каждом из трех районов города по 20 компьютерных клубов. Стоимость одного часа работы компьютеров различна в зависимости от их марки и приведена в следующей таблице для одного клуба.

Количество	10	20	15
компьютеров a	10	20	15
компьютеров a
Стоимость
одного часа	0,5	0,6	0,4
работы (усл. ед)	0,5	0,6	0,4
работы (усл. ед)

b
	12

Какую выручку имеет бизнесмен за один час работы всех компьютерных клубов?

РЕШЕНИЕ:

Вычислим выручку от работы одного компьютерного клуба. Эта выручка численно равна скалярному произведению векторов вида

a (10;20;15) и b (0,5;0,6;0,4) , т.е.

a • b =10 0,5 20 0,6 150,4 5 12 6 23 (усл. ед.).

Т.к. клубов в каждом районе по 20, а районов три, то общая выручка составит: 3 20 23 1320(усл. ед.) за один час работы всех клубов города.

Задания для решения:

1. Вычислить модуль вектора a = (6; 3; –2).

		= 13.
2. Путь a = (4; –12; z). Вычислить z, если	a	= 13.

3.Даны точки A(3; –1; 2) и B(–1; 2; 1) . Найти координаты векторов AB

иBA .

Найти координаты точки N,

которой

совпадает

конец вектора

a = (3; –1; 4), если его начало совпадает с точкой М(1; 2; –3).

Найти координаты начала вектора

(2; –3; –1),

если его конец

совпадает с точкой (1; –1; 2).

= 450,

= 600,

= 1200.

Дан

модуль

вектора

углы

Вычислить проекции вектора a на координатные оси.

Пусть

Построить

каждый из следующих

векторов

1) a

+ b ; 2)

a – b ; 3) b

– a

; 4) – a

– b .

По

данным

векторам

построить

каждый

из

следующих

векторов 1) 3 a ; 2) –

b ; 3) 2 a +

b ; 4)

a – 3 b .

Даны два вектора a

= (3;–2;6) и b = (–2;1;0). Вычислить проекции на

;

координатные оси следующих векторов: 1) a

b ;

2) a –

3) 2 a ; 4) –

b ; 5) 2 a

+ 3 b ; 6)

– b .

10. Проверить коллинеарность векторов

= (–6;3;–9).

= (2;–1;3) и b

Установить, какой из них длиннее другого и во сколько раз, как они

направлены – в одну или в противоположные стороны.
	11.	При	каких	значениях ,	векторы
	11.	При	каких	значениях ,	векторы	a	= –2 i	– 3 j –	k и

b =	i	– –6 j	+ 2 k	коллинеарны?
					13

12. Вычислить модули суммы и разности	векторов

b = (-1;1;–4).
13. Вычислить косинус угла, образованного	векторами

a = (3;–5;8)

a =(2; -4; 4)

b =(-3; 2; 6).

14. Даны вершины треугольника А(-1; -2; 4), В(4; -2; 0) и С(3; -2; 1). Определить его внутренний угол при вершине В.

15.	Даны вершины треугольника А(3; 2; -3), В(5; 1; 1) и С(1; -2; 1).
Определить его внешний угол при вершине А.
16.
	Вычислить проекцию вектора a	(5; 2; 5) на ось вектора b (2; -1; 2) .

Тема 1.5 Векторное и смешанное произведения векторов, их вычисление и приложения.

Векторное произведение двух векторов

Определение. Векторным произведением двух векторов a и b называется вектор c , для которого:

1) c a b sin ( a , b );

2)c перпендикулярен плоскости, в которой можно расположить a и b ;

3)из конца вектора c кратчайший поворот от a к b виден как поворот против часовой стрелки.

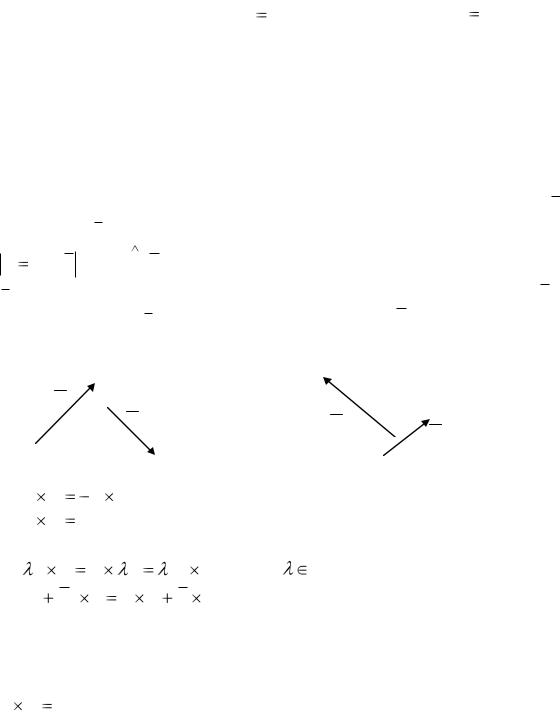
Пусть даны два вектора:

б)

Свойства векторного произведения двух векторов a и b ,

a ;

0 тогда и только тогда, когда хотя бы один из векторов a

или b равен 0 или они коллинеарны;

R ;

(a b ) , здесь

4) (a b ) c a c b c .

Если два вектора заданы своими координатами в ортонормированном

базисе, т.е. a = x1 i

+ y1 j

+ z1 k , b = x2 i

+ y2 j

+ z2 k , то

a b

В частности, из определения векторного произведения видно, что модуль a b численно равен площади параллелограмма, построенного на векторах-сомножителях, а площадь треугольника – половине этого модуля. Другими словами, справедливы следующие формулы:

			1
S	a b	и S	1	a b	.
S	a b	и S	2	a b	.
			2

Смешанное произведение трех векторов

Определение. Смешанным произведением трех векторов a , b , c называется число, которое получается при скалярном произведении векторов a b и c .

Оно обозначается a b c . Иногда используются и другие обозначения, например, a b c или ( a , b , c ).

Из приведенного определения смешанного произведения трех векторов вытекают следующие свойства:

1) a b c 0 тогда и только тогда, когда a , b , c компланарны. Отметим, что это свойство часто используется как условие компланарности трех векторов;

2) a b

c a

c ;

3) a b

= b

a =

a b = – b a

= –

b a = – a

b .

Пусть заданы три вектора:

a = x1 i

+ y1 j + z1 k , b = x2 i

+ y2 j + z2 k ,

= x3 i + y3

j + z3 k . Тогда

x1 y1 z1 a b c x2 y2 z2 .

x3 y3 z3

x1 y1 z1

Свойство 1 можно записать в виде: x2 y2 z2 0 .

x3 y3 z3

Из определения смешанного произведения трех векторов следует, что его модуль равен объему параллелепипеда, построенного на векторах-

сомножителях, т.е. V= a b c .

c b

Образцы решения задач:

ПРИМЕР.

	Вычислить площадь параллелограмма, построенного на векторах

a = -2 i + 3 j + 6 k и b = 6 i –2 j + 3 k .
РЕШЕНИЕ:
	Найдем

	i			j	k					3 6			2 6			2 3
	i			j	k


a b		2 3 6					i					j			k			21i	42 j 14k .
	6		2		3					2	3		6	3		6	2
	6		2		3												49(ед.2)


											212		422		14)2
	Тогда S					a			b		212		422	(	14)2
	В		физике					векторное					произведение				можно		использовать для

вычисления момента и установления направления равнодействующей силы, составляющими которой являются несколько сил.

ПРИМЕР. Пусть две силы F1 =(4; 1; 3) и F2 =(-2; 2; 1) приложены в точке А

(6,-6,-3). Вычислить величину и направляющие косинусы момента равнодействующей этих сил относительно точки В (5,-8,-5).

РЕШЕНИЕ: Известно, что момент М равнодействующей сил равен модулю


векторного произведения векторов т.е.													M				M	BA			F .



Найдем координаты векторов F															F1 F2			и BA . Получим F (2;3;4) ,

	BA	(1;2;2) .

					i		j	k			2	2				1	2			1	2
					i		j	k

M = BA F					1 2			2		i				j					k			2i k ,
					2	3		4			3	4				2	4			2	3
					2	3		4


				22		1 2
	M		M	22		1 2			5 .

Направляющие косинусы равнодействующей силы вычислим по формулам

(4). В нашем случае имеем


cos =	2	; cos = 0 ; cos =	1	.

	5		5

ПРИМЕР.

Пусть некоторое твердое тело вращается вокруг неподвижной оси l c

угловой скоростью

-2 i

+ 5 j

+2 k . Вычислить величину скорости

вращения

точки А этого тела, если радиус-вектор OA =3 i

+ j

-2 k , где О

принадлежит оси вращения. РЕШЕНИЕ:

Согласно формуле Эйлера


		i			j	k		5	2		2 2			2 5
		i			j	k

V	OA		2 5			2	i			j			k			12i 2 j 17k ;
V	OA		2 5			2	i			j			k			12i 2 j 17k ;
		3		1		2		1	2		3	2		3	1
		3		1		2

( 12)2 22 ( 17)2 144 4 289 437 .

ПРИМЕР.

Даны вершины тетраэдра А(4; 5; -3), В(6; 3; 0), С(8; 5; -9),

D (-3; -2; -10). Вычислить длину его высоты, опущенной из вершины D. РЕШЕНИЕ:

Вычислим координаты следующих векторов: AB (2; -2; 3), AC (4; 0;

-6), AD (-7; -7; -7).

Вычислим смешанное произведение этих векторов:

			2		2	3		2	3		2	2
			2		2	3

( AB, AC, AD)			4		0	6	4			6
			7		7	7		7	7		7	7
			7		7	7
4(14	21)	6(		14	14)	4	35	6	28	140		168	308.

Тогда объем V тетраэдра будет равен одной шестой модуля смешанного произведения, т.е.

V	1		308	51	1	(ед. куб.).


	6			3

Искомую длину высоты h вычислим используя формулу
V	1	Sh , где S-				площадь основания. Площадь S вычислим по

	3

формуле

													1
											S		1		AB				AC	.
В нашем случае											S	2			AB				AC	.




				i			j		k		2 3							2 3					2	2
				i			j		k


	AB AC =			2			2 3			i							j					k			12i 24 j 8k
				4		0		6			0	6						4	6				4	0
				4		0		6				и


							1									1					1			14 .(ед.2)
					S		1	122 242				82				1		784			1	28
					S	2		122 242				82		2				784			2	28
						2								2							2
Следовательно,
h		3V	3 154					11(лин. ед.).

		S	3 14
		S	3 14

Задания для решения:

1. Вычислить, какую работу производит сила f =(3; -2; -5), когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А(2; -3; 6)

в положение B(3; -2; -1).
2. Даны силы M(3; - 4; 2),	N(2; 3; - 5)	и	P(3; - 2; 4)	, приложенные к одной

точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из

положения М1(5; 3; -7) в положение М2(4; -1; -4).

π/6. Зная, что

=6,

=5,

Векторы a

b образуют угол

вычислить |[ a, b ]|.

Даны:

=10,

=2 и a

• b =12. Вычислить |[ a, b ]|.

Даны:

=3,

=26 и |[ a, b ]|=72. Вычислить a

• b .

Сила P =(2; -4; 5) к точке М (4; -2; 3). Определить момент этой силы

относительно точки А (3; 2; - 1).

Сила P =(2; 2; 9) приложена к точке A(4; 2; -3).Определить величину и

направляющие косинусы момента этой силы относительно точки С (2; 4; 0).

8. Даны три силы M =(2; -1; -3),	N	=(3; 2; -1) и	P =(-4; 1; 3),

приложенные к точке С(-1; 4; -2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки

D(2; 3; -1).

9.	Даны вершины треугольника А (1;-1; 2), (5; -6; 2) и С(1; 3; -1).
Вычислить длину его высоты, опущенной из вершины В на сторону АС.

10. Даны векторы a (1; -1; 3) ,			b	(-2; 2;1) , c	(3; - 2; 5) . Вычислить abc
11.	Установить,	компланарны	ли	векторы
					a , b , c	если a (2; 3; -1) ,
		(1; 9;11) ;
b (1; -1; 3) , c

12.Доказать, что точки А(1; 2; -1), В(0; 1; 5), С(- 1; 2; 1), D(2; 1; 3) лежат в одной плоскости.

13.Вычислить объем тетраэдра, вершины которого находятся в точках

А ( 2 ; - 1 ; 1 ) , В ( 5 ; 5 ; 4 ) , С ( 3 ; 2 ; - 1 ) и D (4: 1 : 3 ) .

14. Объем тетраэдра V=5, его вершины находятся в точках A(2; 1; -1), В(3; 0; 1), С(2; -1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси Оу.

Тема 1.6 Прямая линия на плоскости. Задачи на составление уравнений прямых на плоскости и взаимное расположение прямых на плоскости.

Прямая на плоскости. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой на плоскости.

Линии второго порядка

Уравнение

Общее уравнение

Уравнение прямой в

Каноническое

прямой,

прямой

отрезках

уравнение прямой

проходящей через

данную точку

перпендикулярно

данному вектору

А(0;b)

B(а;0)

x x0

y y0

l :Ax By C 0

l :

x y

l :

l : A(x x0 ) B(y y0 ) 0

Параметрические

Уравнение прямой,

Уравнение прямой с

Уравнение прямой,

уравнения прямой

проходящей через

угловым

проходящей через две

данную точку в

коэффициентом

точки

данном

А(х1;y1) и B(x2;y2)

направлении

M(x;y)

N(0;b)

Рисунок 2

b , где

m t

Рисунок 3

l :

, t R

Рисунок 1

– угловой

y y0

n t

x x1

y y1

k (x

x0 )

коэффициент

l :

Образцы решения задач:

ПРИМЕР. Даны две точки М (2; 3) и N (–1; 0). Составить уравнение прямой, проходящей через точку М перпендикулярно отрезку MN . РЕШЕНИЕ:

Найдем координаты вектора MN :

MN = (хN – xM; yN – yM) = ( –1–2; 0 –3) = (–3; –3).

По условию вектор MN является нормальным вектором искомой прямой. Составим равнение прямой, проходящей через данную точку М (2; 3) с

данным нормальным вектором MN = ( –3; –3) :

–3 (х – 2) –3 (у –3) = 0 или х + у – 5 = 0 – уравнение искомой прямой.

ПРИМЕР. Определить параметры k и b прямых: 2х + 5у – 10 = 0; 3у + 7 = 0; 4х – 9у = 0.

РЕШЕНИЕ:

Разрешим первое уравнение относительно у, получим:

y	2	x	10		или y		2	x 2 .
y	5	x		5	или y		5	x 2 .
	5			5			5
Сравнивая это уравнение с уравнением y						k x b , находим k			2	, b 2 .
Сравнивая это уравнение с уравнением y						k x b , находим k				, b 2 .
						1			5	1
									5

Разрешив два других уравнения относительно у, получим:

y	7		, откуда k			0, b				7	;
y			, откуда k	2		0, b					;
	3			2		2				3
	3									3
y	4	x , откуда		k			4	, b		0 .
y		x , откуда		k	3			, b		0 .
	9				3	9			3
	9					9

ПРИМЕР. Найти отрезки, отсекаемые на осях координат прямыми:

7х + 2у – 14 = 0; 2х – 3у – 6 = 0.

РЕШЕНИЕ:

Разделим первое уравнение на 14, а второе на 6 и перенесем свободные члены в правые части. Сравнивая полученные уравнения с уравнением в

отрезках на осях	x	y	1		, находим соответственно:

	a	b
	a	b
						x			y	1,		a1	2, b1	7 ;

					2		7
					2		7
				x				y			1,	a2	3, b2	2 .

			3				2
			3				2

ПРИМЕР. Написать уравнение прямой, проходящей через точку М (–2, 3) и параллельной биссектрисе второго координатного угла.

РЕШЕНИЕ:

Искомая прямая, как и биссектриса второго координатного угла, образует с

положительным направлением оси Ох угол					1350 , поэтому k			tg1350		1.
Так	как	точка	М	дана,	то	x1	2, y1	3.	Тогда
уравнение y		y0 k (x	x0 ) при k	1, x1	2, y1	3 принимает вид
		y	3 1(x	( 1)), y	3	x 2
				20

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.03.20161.14 Mб108ЛЕКЦИЯ- УГЛЕВОДЫ 5.5.2013.doc
#
15.03.2016264.7 Кб79Лекция4 ВХБ.doc
#
09.04.2015131.7 Кб41Лопатин.docx
#
09.04.201539.2 Кб15Маркетинг и ценообразование.docx
#
15.03.2016217.21 Кб27маркетинг и цо(1).docx
#
09.04.20153.54 Mб17математика Раздел1 практика.pdf
#
15.03.2016328.19 Кб28матер. метук. 2007.doc
#
09.04.201528.11 Кб8мгуп.docx
#
09.04.201523.02 Кб45МГУП1.docx
#
15.03.20161.08 Mб658МЕТ УКАЗАНИЯ ОБЩАЯ ХИМИЯ.doc
#
15.03.2016790.02 Кб19Мет. рек. КР 2012 (заочники).doc